第九届蓝桥杯大赛个人赛决赛（C/C++大学B组）

第九届蓝桥杯大赛个人赛决赛（C/C++大学B组）

第一题 换零钞（11分）

x星球的钞票的面额只有：100元，5元，2元，1元，共4种。
小明去x星旅游，他手里只有2张100元的x星币，太不方便，恰好路过x星银行就去换零钱。
小明有点强迫症，他坚持要求200元换出的零钞中2元的张数刚好是1元的张数的10倍，
剩下的当然都是5元面额的。

银行的工作人员有点为难，你能帮助算出：在满足小明要求的前提下，最少要换给他多少张钞票吗？
（5元，2元，1元面额的必须都有，不能是0）

注意，需要提交的是一个整数，不要填写任何多余的内容。

• 答案：74

思路：暴力枚举

1. 暴力枚举100元张数x、5元张数y、1元张数z，确定了1元张数也就确定了2元张数
2. 满足条件100x+5y+21z==200即为符合要求的组合
3. sum=min{x+y+11z|100x+5y+21z==200}，即求符合要求的最小张数

• 该题可能还有其他解法，但是由于是填空题，问题规模小，暴力法已经适用，无需花时间想复杂度更低的解法，节省时间做其他题目

代码实现

#include
#include
using namespace std;

int main(){
     
	int x,y,z,sum=200,t;	//100元、5元、1元张数。sum记录总张数 
	for(int i=0;i<2;i++){
     
		for(int j=1;j<40;j++){
     
			for(int k=1;k<10;k++){
     
				if(100*i+5*j+21*k==200){
     
					t=i+j+11*k;
					if(t<sum){
     
						sum=t;
						x=i,y=j,z=k;
					}
				}
			} 
		}
	}
	if(sum==200) cout<<"没有符合要求的组合";
	else cout<<sum<<" (x,y,z):("<<x<<","<<y<<","<<z<<")";
	return 0; 
} 

第二题 激光样式（35分）

x星球的盛大节日为增加气氛，用30台机光器一字排开，向太空中打出光柱。
安装调试的时候才发现，不知什么原因，相邻的两台激光器不能同时打开！
国王很想知道，在目前这种bug存在的情况下，一共能打出多少种激光效果？

显然，如果只有3台机器，一共可以成5种样式，即：
全都关上（sorry, 此时无声胜有声，这也算一种）
开一台，共3种
开两台，只1种

30台就不好算了，国王只好请你帮忙了。

要求提交一个整数，表示30台激光器能形成的样式种数。

注意，只提交一个整数，不要填写任何多余的内容。

• 答案：2178309

思路：DFS

1. 每一台灯都有关/开两种状态
2. 当前层的灯是打开的，则进入下二层；当前层的灯是关的，则进入下一层
3. 当层数超过30层的时候返回1
4. 记录每个子问题的解的个数将其和返回

代码实现

#include
#include
using namespace std;

int dfs(int deep){
     			//deep表示正在进行选择开/关的灯号 
	if(deep>30) return 1;	//递归出口，30台机器设置完成就返回一个结果
	int sum;
	sum=dfs(deep+2);		//当前这台灯打开了 
	return sum+dfs(deep+1);	//当前这台灯关闭了 
} 

int main(){
     
	cout<<dfs(1); 
	return 0;
}

第三题 格雷码(27分)

格雷码是以n位的二进制来表示数。
与普通的二进制表示不同的是，它要求相邻两个数字只能有1个数位不同。
首尾两个数字也要求只有1位之差。

有很多算法来生成格雷码。以下是较常见的一种：
从编码全0开始生成。
当产生第奇数个数时，只把当前数字最末位改变（0变1，1变0）
当产生第偶数个数时，先找到最右边的一个1，把它左边的数字改变。
用这个规则产生的4位格雷码序列如下：
0000
0001
0011
0010
0110
0111
0101
0100
1100
1101
1111
1110
1010
1011
1001
1000

以下是实现代码，仔细分析其中逻辑，并填写划线部分缺少的代码。

#include 
void show(int a,int n)
{
     
	int i;
	int msk = 1;
	for(i=0; i<n-1; i++) msk = msk << 1;
	for(i=0; i<n; i++){
     
		printf((a & msk)? "1" : "0");
		msk = msk >> 1;
	}
	printf("\n");
} 

void f(int n)
{
     
	int i;
	int num = 1;
	for(i=0; i<n; i++) num = num<<1;
	
	int a = 0;
	for(i=0; i<num; i++){
     
		show(a,n);
		
		if(i%2==0){
     
			a = a ^ 1;
		}
		else{
     
			a = _________________________ ; //填空
		}
	}
}

int main()
{
     
	f(4);
	return 0;
}

请注意：只需要填写划线部分缺少的内容，不要抄写已有的代码或符号。

• 答案：a^((a&(-a))<<1)

思路：观察法

1. 按照题目描述有

   • 当产生第奇数个数时，只把当前数字最末位改变（0变1，1变0）
   • 当产生第偶数个数时，先找到最右边的一个1，把它左边的数字改变

2. 观察main方法，发现num表示可生成的格雷码总数，show方法打印a对应的n位长度格雷码

3. 后面的show后面的判断语句是为下次打印a对应的格雷码而修改a的值

4. 代码if(i%2==0)判断是否为偶数，但是前面已经打印过a了，故此操作是判断下一次循环的奇偶性的，下次循环为奇数时，if条件为真，故a值被改变为a^1（利用异或运算最后一位取反）

5. 故else的时候应该对应下次循环为偶数时修改a的值

6. 观察运行结果（如下）可以发现所有下标i除以2以后为奇数的情况下都反转倒数第二位；所有下标i除以2为偶数的都反转位置满足如下情况：idx=2+i/4，若idx<=n,则反转倒数idx位，若idx>n,则反转正数idx-n位

   格雷码	  i  i/2 i/4 	  变化位
   0000	0	0			-
   0001	1				末位
   0011	2	1			倒数第二位
   0010	3				末位
   0110	4	2	1		倒数第3位	3=2+1
   0111	5				末位
   0101	6	3			倒数第二位
   0100	7				末位
   1100	8	4	2		倒数第四位	4=2+2
   1101	9				末位
   1111	10	5			倒数第二位
   1110	11				末位
   1010	12	6	1		倒数第3位	3=2+1
   1011	13				末位
   1001	14	7			倒数第二位
   1000	15				末位
   

7. 由上分析可以得出变化规律，但是由于在第i次循环中改变第i+1次输出的a值，故所有1都要加上1再进行计算

8. 可以得出偶数位的a的迭代表达式为(i+1)/2%2?a^2:(a(2<<((i+1)/4>n-2?2*(n-2)-(i+1)/4:(i+1)/4)))

9. 化简上式得到答案 (i+1)/2%2?a^2:(a(2<<((i+9)/4>n?2*n-(i+17)/4:(i+1)/4)))

• 上述结果仅对f的参数为4的时候正确，一旦将参数填成5、6…都错误

改进思路：根据算法描述填空

1. 上面已经分析出空格位置是找到最右边的一个1，把它左边数字改变，按照这个思路填写即可

2. 由于空格只有一行，没法写循坏语句，但是可以用嵌套条件运算解决

3. 将a从最后一位一直往前按位与，直到与的结果不为0为止，将这个位置的前一位取反

4. 由于int是32位的，最长往前32位

5. 故得到如下答案

   a^(1<<(a&(1<<0)?1:a&(1<<1)?2:a&(1<<2)?3:a&(1<<3)?4:a&(1<<4)?5:a&(1<<5)?6:a&(1<<6)?7:a&(1<<7)?8:a&(1<<8)?9:a&(1<<9)?10:a&(1<<10)?11:a&(1<<11)?12:a&(1<<12)?13:a&(1<<13)?14:a&(1<<14)?15:a&(1<<15)?16:a&(1<<16)?17:a&(1<<17)?18:a&(1<<18)?19:a&(1<<19)?20:a&(1<<20)?21:a&(1<<21)?22:a&(1<<22)?23:a&(1<<23)?24:a&(1<<24)?25:a&(1<<25)?26:a&(1<<26)?27:a&(1<<27)?28:a&(1<<28)?29:a&(1<<29)?30:a&(1<<30)?31:32))

• ps:别嫌代码太长，都是重复代码，写个程序输出一下就好了

改进思路：利用补码取反

1. 这道题的关键是找出从末位开始往前的第一个1，像二进制数0x10011000要找出的是最后4位即找到0x00001000再左移一位得到0x00010000再与a按位异或就得到想要的值了
2. 回忆计算机组成原理中的内容，补码取反的时候可以保持最后一位1以及往后的0都不变，前面全部取反，如果这个取反的数字与原数按位与就可以得到最后一位1和后面的所有0了
3. 由上分析可以得到答案a^((a&(-a))<<1)

完整代码与注释

#include 
void show(int a,int n)
{
     
	int i;
	int msk = 1;
	for(i=0; i<n-1; i++) msk = msk << 1;	//先将1左移n位变成 Ox1000..0(n-1个0） 
	for(i=0; i<n; i++){
     
		printf((a & msk)? "1" : "0");		//打印a的第二进制表示第i位的数值 
		msk = msk >> 1;
	}
	printf("\n");
} 

void f(int n)		//n表示生产的格雷码的长度 
{
     
	int i;
	int num = 1;
	for(i=0; i<n; i++) num = num<<1;	//把1左移n位，num表示可生成的格雷码总数 
	
	int a = 0;
	for(i=0; i<num; i++){
     
		show(a,n);						//打印a对应的n位长度格雷码 
		
		if(i%2==0){
     						//i为偶数，即下一次循环开始时i为奇数 
			a = a ^ 1;					//利用按位异或运算将a的末位（二进制表示）改变 
		}
		else{
     							//对应的就是下次循环开始是i为偶数 
			a = a^((a&(-a))<<1); //填空	（利用补码取反的技巧找到最右边的一个1，把它左边的数字改变） 
		}
	}
}

int main()
{
     
	f(4);		
	return 0;
}

第四题 调手表（45分）

小明买了块高端大气上档次的电子手表，他正准备调时间呢。
在 M78 星云，时间的计量单位和地球上不同，M78 星云的一个小时有 n 分钟。
大家都知道，手表只有一个按钮可以把当前的数加一。在调分钟的时候，如果当前显示的数是 0 ，那么按一下按钮就会变成 1，再按一次变成 2 。如果当前的数是 n - 1，按一次后会变成 0 。
作为强迫症患者，小明一定要把手表的时间调对。如果手表上的时间比当前时间多1，则要按 n - 1 次加一按钮才能调回正确时间。
小明想，如果手表可以再添加一个按钮，表示把当前的数加 k 该多好啊……
他想知道，如果有了这个 +k 按钮，按照最优策略按键，从任意一个分钟数调到另外任意一个分钟数最多要按多少次。
注意，按 +k 按钮时，如果加k后数字超过n-1,则会对n取模。
比如，n=10, k=6 的时候，假设当前时间是0，连按2次 +k 按钮，则调为2。

「输入格式」
一行两个整数 n, k ，意义如题。

「输出格式」
一行一个整数
表示：按照最优策略按键，从一个时间调到另一个时间最多要按多少次。

「样例输入」
5 3

「样例输出」
2

「样例解释」
如果时间正确则按0次。否则要按的次数和操作系列之间的关系如下：
1：+1
2：+1, +1
3：+3
4：+3, +1

「数据范围」
对于 30% 的数据 0 < k < n <= 5
对于 60% 的数据 0 < k < n <= 100
对于 100% 的数据 0 < k < n <= 100000

资源约定：
峰值内存消耗（含虚拟机） < 256M
CPU消耗 < 1000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。

注意：
main函数需要返回0;
只使用ANSI C/ANSI C++ 标准;
不要调用依赖于编译环境或操作系统的特殊函数。
所有依赖的函数必须明确地在源文件中 #include
不能通过工程设置而省略常用头文件。

提交程序时，注意选择所期望的语言类型和编译器类型。

思路：动态规划

1.假设距离目标还差d步，有两种选择：a.走一步，剩下距离s=d-1步 b.走k步，剩下距离s=d-k>=0?d-k:n+d-k
2.若剩下距离s>d,毫无疑问走一步更快，因为走k步以后更远了
3.状态转移方程 dp[d]=1+min(dp[d-1],dp[d-k>=0?d-k:n+d-k 4.对于 d-k >= 0 ? d-k : n+d-k < d ? n+d-k : d-1这个条件，可以化简，其中n+d-kk的，故必为假，故状态转移方程化简为了 dp[d]=1+min(dp[d-1],dp[d>=k?d-k:d-1])
5.初始状态dp[0]=0代表距离0步时无需按按钮
6.从dp[1]开始计算到dp[n-1],max(dp[i])(0

代码实现

#include
using namespace std;

int main(){
     
	int n,k,*dp,s,result=0;
	cin>>n>>k;
	dp=new int[n];
	dp[0]=0;	//初始条件
	//利用状态转移方程填表 
	for(int i=1;i<n;i++)
		dp[i]=1+min(dp[i-1],dp[i>=k?i-k:i-1]);
	//计算其中最大值 
	for(int i=0;i<n;i++)
		result=max(result,dp[i]);
	cout<<result;
	return 0; 
} 

第五题 搭积木（77分）

小明对搭积木非常感兴趣。他的积木都是同样大小的正立方体。
在搭积木时，小明选取 m 块积木作为地基，将他们在桌子上一字排开，中间不留空隙，并称其为第0层。
随后，小明可以在上面摆放第1层，第2层，……，最多摆放至第n层。摆放积木必须遵循三条规则：

规则1：每块积木必须紧挨着放置在某一块积木的正上方，与其下一层的积木对齐；
规则2：同一层中的积木必须连续摆放，中间不能留有空隙；
规则3：小明不喜欢的位置不能放置积木。

其中，小明不喜欢的位置都被标在了图纸上。图纸共有n行，从下至上的每一行分别对应积木的第1层至第n层。每一行都有m个字符，字符可能是‘.’或‘X’，其中‘X’表示这个位置是小明不喜欢的。
现在，小明想要知道，共有多少种放置积木的方案。他找到了参加蓝桥杯的你来帮他计算这个答案。
由于这个答案可能很大，你只需要回答这个答案对1000000007(十亿零七)取模后的结果。
注意：地基上什么都不放，也算作是方案之一种。

【输入格式】
输入数据的第一行有两个正整数n和m，表示图纸的大小。
随后n行，每行有m个字符，用来描述图纸 。每个字符只可能是‘.’或‘X’。

【输出格式】
输出一个整数，表示答案对1000000007取模后的结果。

【样例输入1】
2 3
…X
.X.

【样例输出1】
4

【样例说明1】
成功的摆放有（其中O表示放置积木）：
(1)
…X
.X.
(2)
…X
OX.
(3)
O.X
OX.
(4)
…X
.XO

【样例输入2】
3 3
…X
.X.
…

【样例输出2】
16

【数据规模约定】
对于10%的数据，n=1，m<=30；
对于40%的数据，n<=10，m<=30；
对于100%的数据，n<=100，m<=100。

资源约定：
峰值内存消耗（含虚拟机） < 256M
CPU消耗 < 1000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。

注意：
main函数需要返回0;
只使用ANSI C/ANSI C++ 标准;
不要调用依赖于编译环境或操作系统的特殊函数。
所有依赖的函数必须明确地在源文件中 #include
不能通过工程设置而省略常用头文件。

提交程序时，注意选择所期望的语言类型和编译器类型。

思想：动态规划

1. 预处理：将所有‘x’及其上方的数据改为0，其余的为1，方便判断
2. 从底部开始往上统计该层存在的组合
3. 维护表dp[i] [k] [j]表示第i层j位置其到k位置存在的组合数
4. 状态转移方程:dp[i] [k] [j]的计算是上一行的含j开始到k结束的所有可能组合数
   dp[i][k][j]=sum(dp[i-1] [k1] [j1])(jx
5. 初始状态：dp[1] [k] [j]=1
6. 填完表之后sum(dp[i] [k] [j])+1(1表示一个积木也不放)就是所求结果
7. 优化一：在计算完每个dp[i] [k] [j]之后都与sum累加一下赋值给sum可以减少遍历次数
8. 优化二：用两个二维数组交替使用代替三维数组减少内存使用

代码实现

#include
#include
#include
#define MOD 1000000007
using namespace std;

int main(){
     
	int n,m,***dp,sum=1,r,i,j,k,rr,jj,kk;
	cin>>n>>m;
	int map[n+1][m+1];
	char c[m+1];
	//1.接收参数，绘制地图 
	for(i=n;i>0;i--){
     
		cin>>c+1; 
		for(int j=1;j<=m;j++){
     
			if(c[j]=='.') map[i][j]=1;
			else map[i][j]=0;
		}
	} 
	/*********************计时器****************************/
//	clock_t start=clock(); 
	/*********************计时器****************************/
	//2.地图预处理
	bool flag;
	for(j=1;j<=m;j++){
     
		flag=false;
		for(i=1;i<=n;i++){
     
			if(!map[i][j]) flag=true;
			if(flag) map[i][j]=0;	//0上方的所有数组都为0（不可以放积木） 
		}
	}
	//3.确定初始状态
	dp=new int**[2]; 				//两个二维数组循环使用 
	for(i=0;i<2;i++){
     
		dp[i]=new int*[m+1];		//结束位维度
		for(j=1;j<=m;j++){
     
			dp[i][j]=new int[j+1];	//开始位维度 
		} 
	}
	for(i=1;i<=m;i++){
     				//i是开始维度
		if(!map[1][i]) continue; 	//这个开始位置不能放 
		for(int j=i;j<=m;j++){
     		//j是结束维度
			if(!map[1][j]) break; 	//这个结束位置不能放 
			dp[1][j][i]=1;			//dp[1][k][j]=1;
			sum=(sum+dp[1][j][i])%MOD;
		}
	} 
	//4.按照状态转移方程填写表格并计数,每填写完三维表一个位置统计一次（统计完才能被覆盖） 
	for(i=2;i<=n;i++){
     
		r=i&1;												//当前使用的二维表 
		rr=r^1;												//另一张二维表 
		for(j=1;j<=m;j++){
     									//j是开始维度 
			if(!map[i][j]) continue;						//开始位就是不能放积木的 
			for(k=j;k<=m&&map[i][k];k++){
     					//k是结束维度
				dp[r][k][j]=0;								//初始化为0 
				for(jj=j;jj&&map[i-1][jj];jj--){
     			//上一层的左延伸 
					for(kk=k;kk<=m&&map[i-1][kk];kk++){
     		//上一层的右延伸 
						dp[r][k][j]=(dp[r][k][j]+dp[rr][kk][jj])%MOD;	//上一层所有包含k开始到j结束位置的组合数 
					}
				}
				sum=(sum+dp[r][k][j])%MOD;
			}
		}
	}
	cout<<sum; 		//输出计算结果 
	//5.释放空间 
	for(j=1;j<=m;j++){
     
		delete dp[0][j];
		delete dp[1][j];
	}
	delete dp[0];
	delete dp[1];
	delete dp; 
	/*********************计时器****************************/
//	clock_t end=clock();
//	cout<
	/*********************计时器****************************/
	return 0;
}

• 运行以上代码，能较快得出结果，但是发现规模为n=100，m=100时比较容易超时
• 观察代码发现该算法时间复杂度为O（n^5），是个非常恐怖的复杂度，运行时间容易超过1S

优化：去冗余计算

1. 观察上的代码发现在五层循坏的最里层有许多重复的计算，可以考虑去掉这些冗余的计算
2. 优化方法：用record[i] [j]记录当前层一定包含第i位置到j位置，并且从i位置开始往前延伸到不能再放积木的位置为止的所有组合之和，此时dp[i] [k] [j]的计算不再需要对j枚举
3. 优化后的状态转移方程：dp[i] [k] [j]=sum(record[k1] [j])(k<=k10||knn+1)
4. record[i][j]的计算则在计算dp[i-1] [k] [j]时，在对k的循环过程中对dp[i-1] [k] [j]向左延伸求和得到，如此一来省去了大量的冗余计算，并且不需要两张dp表,只需要一张dp表就可以完成计算而不需要互相覆盖,而record表在每次计算中既要记录该层的record，又要使用上一层的record表，故需要两张record表

优化代码实现

#include
#include
#include
#define MOD 1000000007
using namespace std;

int main(){
     
	int n,m,***dp,sum=1,r,rr;
	cin>>n>>m;
	int map[n+1][m+1];
	char c[m+1];
	//1.接收参数，绘制地图 
	for(int i=n;i>0;i--){
     
		cin>>c+1; 
		for(int j=1;j<=m;j++){
     
			if(c[j]=='.') map[i][j]=1;
			else map[i][j]=0;
		}
	} 
	/*********************计时器****************************/
//	clock_t start=clock(); 
	/*********************计时器****************************/
	//2.地图预处理
	bool flag;
	for(int j=1;j<=m;j++){
     
		flag=false;
		for(int i=1;i<=n;i++){
     
			if(!map[i][j]) flag=true;
			if(flag) map[i][j]=0;	//0上方的所有数组都为0（不可以放积木） 
		}
	}
	//3.确定初始状态
	dp=new int**[3]; 				//第一二个二维数组做record使用，第三个数组做dp使用 
	for(int i=0;i<3;i++){
     
		dp[i]=new int*[m+1];		//结束位维度
		for(int j=1;j<=m;j++){
     
			dp[i][j]=new int[j+1];	//开始位维度 
		} 
	}
	for(int i=1;i<=m;i++){
     			//i是开始维度
		if(!map[1][i]) continue; 	//这个开始位置不能放 
		for(int j=i;j<=m;j++){
     		//j是结束维度
			if(!map[1][j]) break; 	//这个结束位置不能放 
			dp[2][j][i]=1;			//第一行所有组合只有1种组合 
			sum=(sum+dp[2][j][i])%MOD;
			dp[1][j][i]=0;
			for(int ii=i;ii&&map[1][ii];ii--)	//记录包含i开始到j结束往左延伸的所有组合之和
				dp[1][j][i]=(dp[1][j][i]+dp[2][j][ii])%MOD; 
		}
	} 
	//4.按照状态转移方程填写表格并计数,每填写完三维表一个位置统计一次（统计完才能被覆盖） 
	for(int i=2;i<=n;i++){
     									//i是当前计算的层数 
		r=i&1;												//当前层使用的record表 
		rr=r^1;												//上一层的record表 
		for(int j=1;j<=m;j++){
     								//j是开始维度 
			if(!map[i][j]) continue;						//开始位就是不能放积木的 
			for(int k=j;k<=m&&map[i][k];k++){
     				//k是结束维度
				dp[2][k][j]=0;								//dp初始化为0
				dp[r][k][j]=0;								//record初始化为0 
				for(int kk=k;kk<=m&&map[i-1][kk];kk++)		//上一层的record右延伸累加计算dp 
					dp[2][k][j]=(dp[2][k][j]+dp[rr][kk][j])%MOD; 
				for(int jj=j;jj&&map[i][jj];jj--)			//更新当前层的record 
					dp[r][k][j]=(dp[r][k][j]+dp[2][k][jj])%MOD;
				sum=(sum+dp[2][k][j])%MOD;
			}
		}
	}
	cout<<sum; 		//输出计算结果 
	//5.释放空间 
	for(int j=1;j<=m;j++){
     
		delete dp[0][j];
		delete dp[1][j];
		delete dp[2][j];
	}
	delete dp[0];
	delete dp[1];
	delete dp[2];
	delete dp; 
	/*********************计时器****************************/
//	clock_t end=clock();
//	cout<
	/*********************计时器****************************/
	return 0;
}

第六题 矩阵求和

经过重重笔试面试的考验，小明成功进入 Macrohard 公司工作。
今天小明的任务是填满这么一张表：
表有 n 行 n 列，行和列的编号都从1算起。
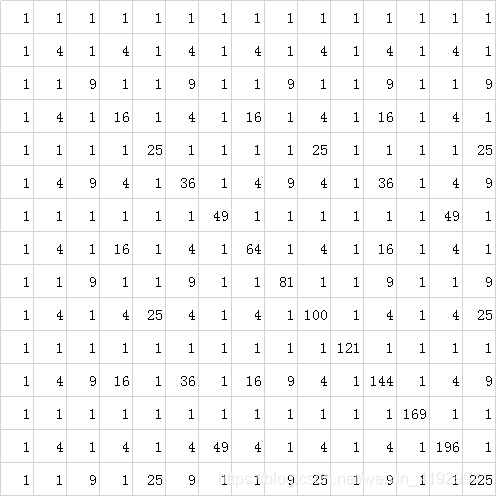
其中第 i 行第 j 个元素的值是 gcd(i, j)的平方，
gcd 表示最大公约数，以下是这个表的前四行的前四列：
1 1 1 1
1 4 1 4
1 1 9 1
1 4 1 16

小明突然冒出一个奇怪的想法，他想知道这张表中所有元素的和。
由于表过于庞大，他希望借助计算机的力量。

「输入格式」
一行一个正整数 n 意义见题。

「输出格式」
一行一个数，表示所有元素的和。由于答案比较大，请输出模 (10^9 + 7)(即：十亿零七) 后的结果。

「样例输入」
4

「样例输出」
48

「数据范围」
对于 30% 的数据，n <= 1000
存在 10% 的数据，n = 10^5
对于 60% 的数据，n <= 10^6
对于 100% 的数据，n <= 10^7

资源约定：
峰值内存消耗（含虚拟机） < 256M
CPU消耗 < 2000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。

注意：
main函数需要返回0;
只使用ANSI C/ANSI C++ 标准;
不要调用依赖于编译环境或操作系统的特殊函数。
所有依赖的函数必须明确地在源文件中 #include
不能通过工程设置而省略常用头文件。

提交程序时，注意选择所期望的语言类型和编译器类型。

思路：快速幂+记忆搜索

1. 对角线是1~n的平方和，剩下两侧算一侧乘以2即可

2. 问题最大规模10^7，用int平方计算溢出，用long long

3. 最大时矩阵共有10^14（一百万亿）个元素，一个个计算仍然不现实 ，填充一部分看看规律
   

4. 规律：矩阵是关于左上到右下对角线对称的，去掉右上部分和对角线后，剩下的所每行都关于各自行的中间对称

5. 利用上诉规律减少计算，大约为原来的1/4，即约25万亿次加法，其次每个质数prim的去掉对称轴和关于对称轴对称的右上部分，剩下部分的和正好为prim-1，可以减去大量的计算

6. 对角线部分的和的计算（sum的初始值）利用平方和公式即可sum=n(n+1)(2n+1)/6,但是考虑到n比较大，需要使用快速幂乘法进行计算过程的取模操作，保证不会溢出

7. 剩余部分需要大量用到质数和平方数，先计算好1~n内的所有质数和平方数能减少计算

代码实现

#include
#include
#define MAX 10000000
using namespace std;

typedef long long LL;
const int MOD=1e9+7;
int pn;			//质数的个数 
int *prim;
LL *square; 

//计算1~n内所有的质数 
int get_prim(int n){
     
	prim = new int[MAX];
	prim[0]=2,prim[1]=3;
	if(n<2) return 0;
	else if(n==2) return 1;
	else if(n==3) return 2;
	int count=2,j;
	for(int i=5;i<=n;i+=2){
     						//去掉所有的偶数 
		for(j=1;(j<count)&&(i%prim[j]);j++);	//第一个质数是2，i不可能是偶数 
		if(j==count&&i%prim[j-1]) prim[count++]=i;
	}
	return count; 
} 

//快速幂乘法 
LL quick(LL a,LL b){
     
	LL result=0;
	while(b){
     
		if(b&1) result+=a;
		a=(a+a)%MOD;
		b=b>>1;
	}
	return result;
}

//对角线平方求和 
LL sq_sum(int n){
     
	LL a=n,b=n+1,c=2*n+1,sum;
	if(a%2==0) 	a/=2;
	else b/=2;
	if(a%3==0)	a/=3;
	else if(b%3==0) b/=3;
	else c/=3;
	sum=quick(b,a);
	return quick(sum,c);
}

void get_square(int n){
     
	square=new LL[n+1];
	for(LL i=1;i<=n;i++){
     
		square[i]=i*i%MOD;
	}
}

//将n阶矩阵最外围除右下角那一个位置，其余值全部相加 
LL lin_sum(int n){
     
	int t=(n-1)/2,tt,nn,pb;
	LL sum=0,temp=0;
	if(n%2==0) sum=square[n/2];
	for(int i=1;i<=t;i++){
     
		tt=i,nn=n,pb=1;
		for(int j=0;j<pn&&tt>=prim[j];j++){
     
			while(tt%prim[j]==0&&nn%prim[j]==0){
     
				tt/=prim[j];
				nn/=prim[j];
				pb*=prim[j];
			}
		}
//		cout<<"i="<
		temp=(temp+square[pb])%MOD;
	}
	sum=(2*sum+4*temp)%MOD;
//	cout<<"n="<
	return sum;
}

int main(){
     
	int n;
	LL sum;
	cin>>n;
	pn=get_prim(n);	//获取1~n内所有质数 
	sum=sq_sum(n);	//对对角线上所有的平方求和 
	get_square(n);
	if(n==1){
     
		cout<<sum;
		return 0;
	}
	sum+=2;
	if(n==2){
     
		cout<<sum;
		return 0;
	}
	for(int i=3;i<=n;i++){
     
		sum=(sum+lin_sum(i))%MOD;
	} 
	cout<<sum;
	return 0;
}