零基础入门数据挖掘 - 二手车交易价格预测 Task2

Task 2 的主要任务为数据探索性分析

一、EDA简介和目的

简介：

EDA（探索性数据分析），是指对已有的数据在尽量少的先验假定下进行探索，通过作图、指标、方程拟合、计算特征量等手段探索数据的结构和规律的一种数据分析方法。不同于初始数据分析，它更集中于检查模型拟合和假设检验所需的假设，以及处理缺少的值，并根据需要进行变量转换。
我个人觉得，这是数据分析的第一环，也是非常重要的一环，后面所有的分析和建模都是基于这一步。

目的：

1、数据整体情况如何？
2、数据缺失情况如何？缺失的数据是放弃还是补充？补充的话采取什么方式补充？
3、异常值情况如何？如何处理？
4、各变量之间的关系如何？预测值与各变量之间的关系如何？

二、Code

2.1 导包及载入数据

import warnings
warnings.filterwarnings('ignore')

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import missingno as msno

data_train = pd.read_csv('used_car_train_20200313.csv', sep=' ')
data_test_a = pd.read_csv('used_car_testA_20200313.csv', sep=' ')

2.2 查看数据基本信息

data_train.sample(10)
data_test_a.head().append(data_test_a.tail())

data_train.shape
data_test_a.shape

data_train.info()
data_test_a.info()

通过上面的步骤，可以对数据有个初步的了解，比如数据的行列数、列数值类型、大体结构、数据完整情况以及各变量的描述性统计等。

2.3 检查数据缺失情况

data_train.isnull().sum()
data_test_a.isnull().sum()

通过缺失检查，发现data_train中model、bodyType、fuelType、gearbox少量缺失，data_test_a中bodyType、fuelType、gearbox，有缺失值的变量应该都会对价格有较大影响。总体来说，数据完整性不错。

空值填充方式：
数量少：可考虑均值、众数等填充，也可通过树模型自己优化。
数量多：考虑删除。

• 可视化分析

# 空值可视化，柱状图
missing = data_train.isnull().sum()
missing = missing[missing > 0]
missing.plot(kind='bar')

# 使用missingno可视化缺失值库
msno.matrix(data_train)

白线越多，代表缺失值越多。

# 柱状图
msno.bar(data_train)

柱子越矮，代表缺失值越多。

通过missingno库，也可以非常直观的看出变量值缺失情况。

2.3 检查数据异常情况

# 查看方式一：统计某一列的值及个数
df['col_name'].value_counts().sort_index()

# 查看方式二：对列进行描述性统计
df.describe()['col_name']

通过上述方式，可以基本判断出异常数据，在对所有列进行查看后，发现notRepairedDamage中有异常值 ‘-’

data_train['notRepairedDamage'].value_counts()

‘-’ 本质也为空值，可以将它置为nan

data_train['notRepairedDamage'].replace('-', np.nan, inplace=True)

然后通过df.isnull().sum()命令可以查看替换后情况，notRepairedDamage的空值由原本的0变成24324（原先‘-’值的个数）

通过异常检测还发现，seller和offerType两个字段类别特征严重倾斜，对预测每什么帮助，可以删除。

# del df['col_name] 与 df.drop() 都可

del data_train['seller']
del data_train['offerType']

删除后，可通过 df.columns 来查看。
对于data_test_a也采取同样处理方式。

数据异常检查通常思路和处理方法参考：
https://blog.csdn.net/weixin_40444270/article/details/108920646

2.4 预测值分布情况

2.4.1 简单查看

data_train['price']

data_train['price'].value_counts().sort_index()

2.4.2 总体分布

机器学习中，以概率分布为核心的研究大都聚焦于正态分布，正态分布只依赖于数据集的两个特征：样本的均值和方差。使用正态分布，预测变量并在一定范围内找到它的概率会变得非常简单。
如果样本不服从正态分布怎么办呢？我们可以将其转化为正态分布，比如：线性变换、Boxcox变换、Yeo-Johnso变换。
当然，也不能盲目的假设变量符合正态分布，除正态分布外，变量也可以服从泊松分布、学生t-分布、二项式分布等。

当样本数据表明质量特征的分布为非正态时，应用基于正态分布的方法会作出不正确的判决。约翰逊分布族即为经约翰变换后服从正态分布的随机变量的概率分布，约翰逊分布体系建立了三族分布，分别为有界、对数正态和无界。

接下来我们看一下数据集符合什么总体分布。无界约翰逊分布？正态分布？对数正态分布？

import scipy.stats as st

y = data_train['price']
plt.figure(1); plt.title('Johnson SU') # 无界约翰逊分布
sns.distplot(y, kde=False, fit=st.johnsonsu)

plt.figure(2); plt.title('Normal') # 正态分布
sns.distplot(y, kde=False, fit=st.norm)

plt.figure(3); plt.title('Log Normal') # 对数正态分布
sns.distplot(y, kde=False, fit=st.lognorm)

price并不服从正态分布，在回归前必须进行转换，可以看出，其与无界约翰逊分布的拟合效果更好。

2.4.3 查看偏度（Skewness）和峰度（Kurtosis）

• 偏度:
  是描述数据分布形态的统计量，其描述的是某总体取值分布的对称性，简单来说就是数据的不对称程度,绝对值越大表明数据分布越不对称，偏斜程度大
  正态分布偏度为0，即数据分布是对称的。若偏度>0，则分布右偏，分布长尾在右。偏度绝对值越大，说明分布的偏移程度越严重（注：左偏/右偏指的是数值拖尾方向，不是峰位置）
• 峰度:
  描述某变量所有取值分布形态陡缓程度的统计量，简单来说就是数据分布顶的尖锐程度(>0尖顶峰, <0平顶峰, =0与正态分布陡峭程度一致)

print("Skewness: %f" % y.skew())
print("Kurtosis: %f" % y.kurt())

结果可得，价格分布右偏、尖顶峰，与图形一致。
我们也可以看一下data_train 数据集中每个变量的偏度和峰度情况。

sns.distplot(data_train.skew(), color='red', axlabel='Skewness')
sns.distplot(data_train.kurt(), color='blue', axlabel='Kurtosis')

2.4.4 查看预测值频数

plt.hist(y, orientation='vertical', color='orange') # 参数orientation决定了是采用纵轴代表频率还是横轴代表频率的展现形式
plt.show()

大于20000的值极少，可以把它们当作特殊值或者异常值处理（填充或删掉）

plt.hist(np.log(y), orientation='vertical', color='orange')
plt.show()

对价格进行log变换后的分布比较均匀，可以进行log变换进行预测，这也是预测问题中常用的方法。

2.5 特征分析

特征分为类型特征和数字特征。
在没有label encoding的数据，可以直接采用df.select_dtypes()的方式来区分。

# 数字特征
numeric_features = df.select_dtypes(include=[np.number])
numeric_features.columns

# 类型特性
categorical_features  = df.select_dtypes(include=[np.object])
categorical_features.columns

但是本例中，有label encoding，所以需要人为的根据实际含义来区分。

numeric_features = ['power', 'kilometer', 'v_0', 'v_1', 'v_2', 'v_3', 'v_4', 'v_5', 'v_6', 'v_7', 'v_8', 'v_9', 'v_10', 'v_11', 'v_12', 'v_13','v_14' ]

categorical_features = ['name', 'model', 'brand', 'bodyType', 'fuelType', 'gearbox', 'notRepairedDamage', 'regionCode']

2.5.1 类别特征分析

1、查看特征nunique分布

for cat_fea in categorical_features:
    print(cat_fea + "的特征分布如下：")
    print("共有{}个不同的值".format(data_train[cat_fea].nunique()))
    print(data_train[cat_fea].value_counts)

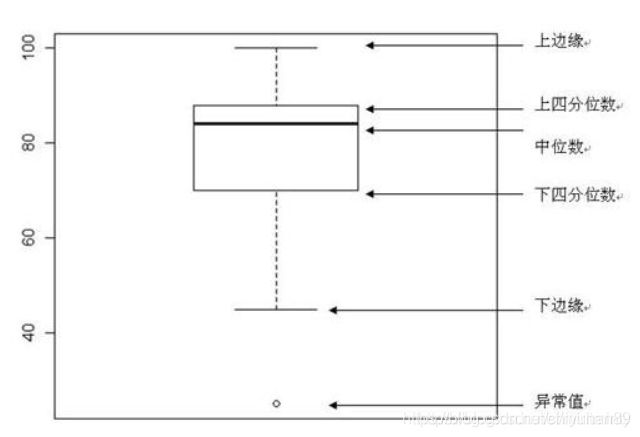
2、类别特征箱形图可视化

• 直观识别数据中的离群点
• 直观判断数据离散分布情况，了解数据分布状态
  

categorical_features = ['model','brand','bodyType','fuelType','gearbox','notRepairedDamage']

# 转为分类数据
for c in categorical_features:
    data_train[c] = data_train[c].astype('category')
    if data_train[c].isnull().any():
        data_train[c] = data_train[c].cat.add_categories(['MISSING'])
        data_train[c] = data_train[c].fillna('MISSING')
        
# 箱型图，主要为了旋转x轴坐标
def boxplot(x, y, **kwargs):
    sns.boxplot(x=x, y=y)
    x = plt.xticks(rotation=90)

f = pd.melt(data_train, id_vars=['price'], value_vars=categorical_features) # price 不需要转换的列
g = sns.FacetGrid(f, col='variable', col_wrap=2, sharex=False, sharey=False, size=5)
g = g.map(boxplot, "value", "price")

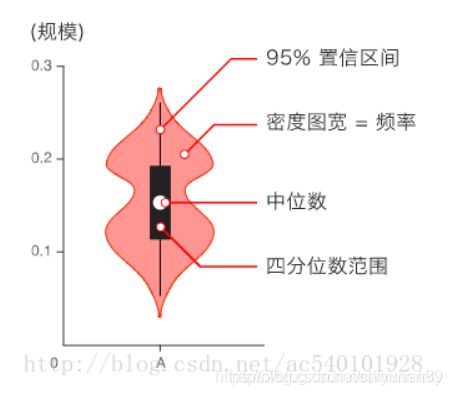
3、类别特征小提琴图可视化

• 用于显示数据分布及概率密度
• 这种图表结合了箱形图和密度图的特征，主要用来显示数据的分布形状
  

for c in categorical_features:
    sns.violinplot(x=c, y='price', data=data_train)
    plt.show()

3、类别特征柱形图可视化

for c in categorical_features:
    sns.barplot(data_train[c], data_train['price'])
    plt.xticks(rotation=90)
    plt.show()
    

黑线为误差条。误差线是通常用于统计或科学数据，显示潜在的误差或相对于系列中每个数据标志的不确定程度。误差线可以用标准差（平均偏差）或标准误差。

• 1）平均值±标准差（Mean±SD）
• 2）平均值±标准误（Mean±SEM）

4、类别特征每个类别频数可视化

def count_plot(x, **kwargs):
    sns.countplot(x=x)
    x = plt.xticks(rotation=90)
    
f = pd.melt(data_train, value_vars=categorical_features)
g = sns.FacetGrid(f, col='variable', col_wrap=2, sharex=False, sharey=False, size=5)
g = g.map(count_plot, "value")

2.5.2 数字特征分析

总览

numeric_features.append('price')
data_train[numeric_features].head()

1、相关性分析

在进行相关性分析之前需要明白三个概念，一是维度，二是协方差，三是相关系数。维度也就是变量。协方差的定义就是$E\{[X-E(X)][Y-E(Y)]\}$，记作Cov(X,Y)，也就是两个维度与各自期望之差的乘积的期望，期望在离散型数据中通常是均值。相关系数就是$Cov(X,Y)/[\sigma (X)\sigma (Y)]$，记作$\rho XY$，其中$\sigma (X)$和$\sigma (Y)$分别表示X和Y的标准差，所以相关系数就是两个变量的协方差除以其标准差之积。
假如某个观测有p个维度，计算每个维度同所有维度之间的协方差，则会形成一个$p\ast p$的矩阵，矩阵的每个数是其相应维度之间的协方差，这个矩阵就称为协方差矩阵，协方差矩阵按照上面的方法再进一步计算就可得到相关关系矩阵。

price_numeric = data_train[numeric_features]
price_numeric.corr()

上述代码可以生成所有维度之间的相关系数。我们把price一列单独拿出来看。

price_numeric.corr()['price'].sort_values(ascending=False)

下面，使用sns.heatmap()进行可视化，热力图对数据集相关系数有很强的可视化效果。

correlation = price_numeric.corr()
f, ax = plt.subplots(figsize=(7,7))
plt.title('Correlation of Numeric Features with Price',y=1,size=16)
sns.heatmap(correlation)

sns.heatmap()常用可选参数:

• annot: 默认为False，True时会在格子上显示数字
• vmax， vmin：热力图颜色取值的最大、最小值，默认会从data中导出。
• square：是否是正方形，默认为True。

2、查看特征偏度和峰度

for col in numeric_features:
    print('{:15}'.format(col), 
         'Skewness: {:5.2f}'.format(data_train[col].skew()), #{:05.2f} 5位宽度、2位小数
         '    ',
          'Kurtosis: {:06.2f}'.format(data_train[col].kurt())  
         )

3、每个数字特征的分布可视化

• pd.melt() ：数据分析的时候，经常要把宽数据转换为长数据，类似列转行。
• sns.FacetGrid() ：无需写循环，绘制多个变量。FacetGrid是seaborn库中的一个类，我们在初始化这个类时只需要给它传一个DataFrame的数据集即可（接受的是长数据）。实例化这个类以后，就可以直接使用这个对象的方法绘制需要的图形。map里面可以是自己定义的函数，也可以是sns、plt等。

f = pd.melt(data_train, value_vars=numeric_features)
g = sns.FacetGrid(f, col="variable",  col_wrap=2, sharex=False, sharey=False)
g = g.map(sns.distplot, "value")

根据结果我们可以看出，匿名特征分布相对均匀。

4、数字特征之间的关系可视化

• sns.pairplot()：通过pair也可以看出，这是展示两两之间关系。对角线上是各个属性的直方图（分布图），可以通过参数diag_kind设置，而非对角线上是两个不同属性之间的相关图。

# 这里是选取前10个与price相关性比较高的来做可视化
columns = ['price', 'v_12', 'v_8' , 'v_0', 'power', 'v_5',  'v_2', 'v_6', 'v_1', 'v_14']
sns.pairplot(data_train[columns], size = 2 ,kind ='scatter',diag_kind='kde')
plt.show()

从图中我们可以看出，v_6和v_1之间具有比较明显的相对关系。

5、多变量与price的回归关系

• sns.regplot()：绘图数据和线性回归模型拟合

2.6 用pandas_profiling生成数据报告

pandas_profiling，这个库只需要一行代码就可以生成数据EDA报告。

import pandas_profiling

pfr = pandas_profiling.ProfileReport(data_train)
pfr.to_file('example.html')

三、总结

这一part花费了我很多时间，也学习到很多。又仔细回顾了很多关于分布的基本知识，以及第一次听说的约翰逊分布…基础实在太薄弱，连pairplot怎么看相关性都要现学，很多百度上找不到的，问了datawahle的助教很多。总之，磕磕绊绊懂了很多，还需继续努力，有了收获还是很开心。真的很感谢助教的帮助！！
统计学的知识一定要好好学，好好学！！是数据分析的灵魂。