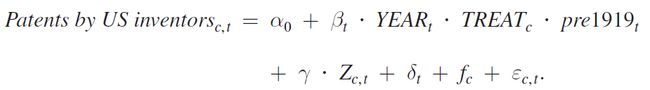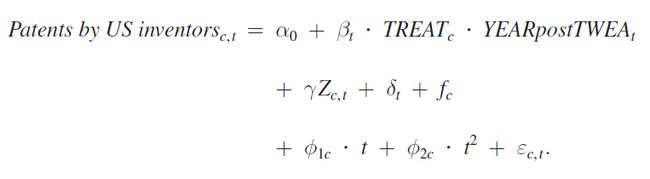python包怎么做双重差分did分析_DID文献复制——Compulsory Licensing
上学期的面板数据分析课程大作业是复制一篇经典文献，我选择了一篇运用DID方法的教科书般的文献——Compulsory Licensing：Evidence from the Trading with the Enemy Act。把复制过程（相当于全文翻译啦）分享给大家，请大家尊重一下我辛辛苦苦的知识版权哦，不要随意转发~
论文介绍
题目 Compulsory Licensing：Evidence from the Trading with the Enemy Act, Petra & Alessandra, ARE, 2012.
研究背景 强制许可制度（Compulsory Licensing）允许发展中国家无需征得专利国同意而使用而生产外国专利产品，但关于该制度的讨论往往忽视了一个重要问题——强制许可效应究竟是促进还是抑制了专利使用国的发明创造水平？
强制许可效应同时具有促进和抑制国内创新的作用机制：促进作用表现在，专利使用国在生产外国专利产品的过程中，可形成自己独立的产品，从而增加了对本国相关产品的研发和技能掌握的创新投资，同时提供了开展“干中学”（具有时滞的特征）的机会；抑制作用表现在，当一国可以在低于市场利率下使用某外国专利时，这就降低了该国的研发本国替代性产品的激励。
研究问题 强制许可制度究竟是促进还是抑制了国内的发明创造水平？
研究方法 可以通过一个外生事件（自然实验）来识别强制许可效应。1917年10月6日，美国国会发布了《敌国贸易法案》（Trading with the Enemy Act, TWEA），该法案允许美国企业侵犯敌国专利，只要这些专利可以为战争做出贡献。
在控制一些可以促进国内创新的变量——例如教育水平、科研培训、关税壁垒等——的基础上，使用双重差分方法（DID）比较受到TWEA影响的科技行业的国内企业专利数量的变化。在排除其他因素的干扰后，可以测度强制许可对国内技术发明的影响。
数据 科技行业选取：美国专利与贸易办公室（United States Patent and Trademark Office, USPOT）的有机化学产业。有机化学行业中共有19个主行业（包含7248个子行业）受到了TWEA的影响，这些类别在1875年至1939年间共产生了128953项专利；336个子行业被作为处理组对待。国内专利数量的变化由该行业中的美国企业的专利授权年度数据来衡量。
主要结果 受到TWEA影响的子行业的国内技术发明得到了极大增长；在TWEA法案出台后，至少得到一个专利授权的子产业， 比未得到强制许可的子行业平均每年多出0.151个技术发明，比平均水平的0.619个技术发明要高出25%。
论文复制（软件版本为stata 16）
一、 TWEA作为强制许可的自然实验
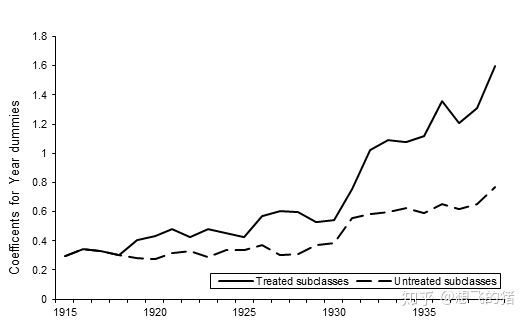
一战期间，德国与美国之间的专利竞争被迫暂停；但在1920年代，德国企业迅速回到了美国市场，并且恢复了专利申请。（见图一）
根据licensed_class的值区分全样本（值为0）和处理组样本（值为1），分别令两个组别的德国专利数量变量（count_ger）对时间虚拟变量td*做不包含截距项的回归，保存回归结果并输出到word文档中。
use "fig1.dta", clear
reg count_ger td* if licensed_class==0, noco
est store all
reg count_ger td* if licensed_class==1, noco
est store treated
esttab all treated using table1.rtf, not根据回归结果，在Office中可绘制下图：
二、 数据
- 解释变量数据：被授权的敌方专利数量
在TWEA影响下，美国共剥夺了超过4500项化工发明相关的外国专利；其中，Chemical Foundation在1919-1926年间将727项外国专利授权给了326家美国企业。被授权的专利覆盖了336个化工类初级和二级子行业，这336个子行业被作为处理组对待。其中，绝大多数的子行业只接受到了一项专利，少数子行业接受的专利数量超过了15项（见图二）；平均而言，每个子行业接受的专利有效期为23年（见图三）。
制作图二。keep命令选择1930年的专利数据，对专利数量(count_cl）变量进行降序排序；在Office中绘制336个对照组的专利数量。
use "chem_patents_maindataset.dta", clear
preserve
keep if grn==1930
gsort -count_cl
browse count_cl
restore
制作图三。keep命令选择1930年的专利数据，对专利数量(count_cl）变量进行降序排序；在Office中绘制336个对照组的专利有效年限。
preserve
keep if grn==1930
gsort -year_conf
browse year_conf
restore
2. 被解释变量数据：美国国内发明创造专利数量
1875-1945年间，在TWEA的影响下，美国化学产业19个主行业（7248个子行业）的国内发明创造专利共计128953项；其中336个子行业被作为处理组对待。国内专利数量通过将总的专利数量减去国外专利数量得到。专利从申请至授权的中位数年限为3年。
3. 测量误差和衰减偏误
测量误差来源：1）专利发明者国籍的分配方式，可能过高估计国内专利数量，但误差较小；2）用以识别国外发明者的光学字符识别方法，可能过高估计国外专利数量，但误差较小（手动收集数据的结果显示，手动方法和算法分配方法的结果差别不大，见表一）；3）USPTO分类方法，专利发明会根据子类别的不同而变化，在回归中控制子类个体效应可解决该问题；另外，假定处理效应只发生在处理组，不考虑处理效应会溢出到其他子行业的话，会低估强制许可效应。
使用tab命令生成手动收集的专利发明国的频率计数，总数为625项；codebook命令查看if条件指定的（算法生成的）专利发明国的专利数量。根据命令运行结果，在Office中可绘制表一。
use "table1.dta"
tab true_nat
codebook patnum if usa==1
codebook patnum if germany==1
codebook patnum if usa==0 & germany==0
三、结果
DID模型设置与OLS回归
该模型为省略控制组和政策发生虚拟变量的简化DID模型，交互项系数仍为标准的双重差分估计量。其中，控制变量Zc,t表示国外发明的专利的总数量；δt和fc表示时间固定效应和子行业的个体固定效应。
根据前文定义的数据，运行如下命令：forvalues循环语句生成年份虚拟变量；xtreg命令作OLS回归，使用子行业层面的聚类标准误处理解释变量序列相关问题，每个回归均包含双向固定效应；outreg2命令将多项回归结果储存在Excel表格中。OLS回归结果如表二所示。
use "chem_patents_maindataset.dta"
forvalues x=1876/1939 {
gen td_`x'=0
qui replace td_`x'=1 if grn==`x'
}
xtreg count_usa treat count_for_2 td*, fe i(class_id) robust cluster(class_id)
outreg2 using ols_table2.xls, replace //（该回归结果未显示在table2中）
xtreg count_usa treat count_for td*, fe i(class_id) robust cluster(class_id)
outreg2 using ols_table2.xls, append //（table2 colume1）
xtreg count_usa treat td*, fe i(class_id) robust cluster(class_id)
outreg2 using ols_table2.xls, append //（table2 colume2）
xtreg count_usa count_cl count_for td*, fe i(class_id) robust cluster(class_id)
outreg2 using ols_table2.xls, append //（table2 colume4）
xtreg count_usa count_cl count_cl_2 count_for td*, fe i(class_id) robust cluster(class_id)
outreg2 using ols_table2.xls, append //（table2 colume3）
xtreg count_usa count_cl td*, fe i(class_id) robust cluster(class_id)
outreg2 using ols_table2.xls, append //（table2 colume5）
xtreg count_usa year_conf year_conf_2 count_for td*, fe i(class_id) robust cluster(class_id)
outreg2 using ols_table2.xls, append //（table2 colume6）
xtreg count_usa year_conf count_for td*, fe i(class_id) robust cluster(class_id)
outreg2 using ols_table2.xls, append //（table2 colume7）
xtreg count_usa year_conf td*, fe i(class_id) robust cluster(class_id)
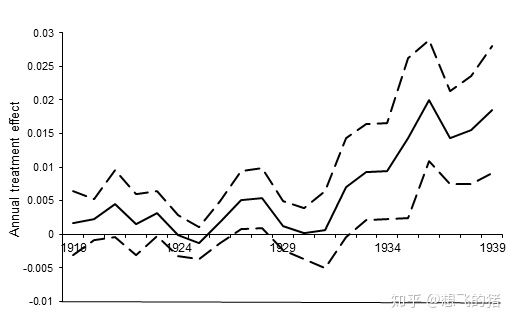
outreg2 using ols_table2.xls, append //（table2 colume8）回归结果显示，强制许可效应与国内专利数量高度相关且统计上显著：得到强制许可的子行业，在1919年以后，平均每年多产生0.151—0.255项专利；即使在控制了外国专利数量以后，处理效应还是很明显，约为平均专利数量0.619的24%。
处理效应估计量β，只有在特定情况下——除了TWEA影响外，对照组和处理组没有其他差异——才是一致估计量。然而，1914年后，德国发明家的效率急剧下降，会对处理组产生较大影响，从而导致β高估了强制许可效应。
为了检测上述“弱竞争”效应，文章对比了处理组和对照组德国发明家的专利数量在TWEA前后的变化。结果显示，虽然1914年后德国发明家的专利数量急剧下降，但在1919年后迅速回升；而且，在处理组中，德国发明家的专利数量并没有在1919年后下降更多，而是迅速回升。
进一步地，专利许可数量的增加使得国内专利数量平均每年增长0.072—0.115项，相当于平均数量的12%—19%；专利剩余年限的增加使得国内专利数量平均每年增长0.006—0.01项。
- 比较事前趋势
双重差分方法基于共同趋势假设：在TWEA发生前，处理组和对照组具有共同的时间趋势。为了检验共同趋势，可估计下述模型：
模型允许β随时间发生变化；选取1900年作为基准线。运行下述命令：forvalues命令产生新的处理组和对照组时间虚拟变量；drop命令删除1900基准年份的时间虚拟变量；xtreg命令对上述模型作OLS回归，标准误使用子行业层面的聚类标准误，回归包含双向固定效应。运行结果包含处理组和对照组的时间趋势以及其95%的置信区间；结果显示，处理组的回归系数绝大多数不显著，说明通过了共同趋势检验；通过Office可绘制图四。
use "chem_patents_maindataset.dta" , clear
forvalues x=1875/1939 {
gen untreat_`x'=1 if licensed==0 & grn==`x'
replace untreat_`x'=0 if untreat_`x'==.
gen treat_`x'=1 if licensed==1 & grn==`x'
replace treat_`x'=0 if treat_`x'==.
}
drop *treat_1900
cap log close //如果有log文件正在运行的话，将它关闭
log using pre.log, replace //开启新的log文件
xtreg count_usa treat_* untreat_*, fe i(class_id) robust cluster(class_id)图四显示，在TWEA发生前，处理组和对照组并无系统性的时间趋势差异，因而共同趋势假设成立。
2. 时滞效应检验
图五给出了TWEA颁布之前，处理组和对照组的美国专利数量占比分布。运行如下命令，可得到美国专利数量占比的分组统计结果，asdoc命令将统计结果保存在word文档中。
use "fig5.dta", clear
asdoc sum share if share>=0 & share<0.1 & licensed_class==0, replace
asdoc sum share if share>=0.1 & share<0.2 & licensed_class==0, rowappend
asdoc sum share if share>=0.2 & share<0.3 & licensed_class==0, rowappend
asdoc sum share if share>=0.3 & share<0.4 & licensed_class==0, rowappend
asdoc sum share if share>=0.4 & share<0.5 & licensed_class==0, rowappend
asdoc sum share if share>=0.5 & share<0.6 & licensed_class==0, rowappend
asdoc sum share if share>=0.6 & share<0.7 & licensed_class==0, rowappend
asdoc sum share if share>=0.7 & share<0.8 & licensed_class==0, rowappend
asdoc sum share if share>=0.8 & share<0.9 & licensed_class==0, rowappend
asdoc sum share if share>=0.9 & share<1 & licensed_class==0, rowappend
asdoc sum share if share==1 & licensed_class==0, rowappend
asdoc sum share if share>=0 & share<0.1 & licensed_class==1, replace
asdoc sum share if share>=0.1 & share<0.2 & licensed_class==1, rowappend
asdoc sum share if share>=0.2 & share<0.3 & licensed_class==1, rowappend
asdoc sum share if share>=0.3 & share<0.4 & licensed_class==1, rowappend
asdoc sum share if share>=0.4 & share<0.5 & licensed_class==1, rowappend
asdoc sum share if share>=0.5 & share<0.6 & licensed_class==1, rowappend
asdoc sum share if share>=0.6 & share<0.7 & licensed_class==1, rowappend
asdoc sum share if share>=0.7 & share<0.8 & licensed_class==1, rowappend
asdoc sum share if share>=0.8 & share<0.9 & licensed_class==1, rowappend
asdoc sum share if share>=0.9 & share<1 & licensed_class==1, rowappend
asdoc sum share if share==1 & licensed_class==1, rowappend根据上述命令运行结果，在Office中可绘制图五。
如果强制许可是通过经验和“干中学”的方式促进国内创新，那么，国内专利数量的显著变化应具有时滞效应。时滞效应可通过估计下述模型进行估计；其中，βt表示，在TWEA颁布之后，处理组和对照组在第t年的专利数量差异。
运行如下命令可分别得到TWEA颁布之后，处理组子行业、专利数量和专利剩余年限对美国专利数量的影响。forvalues命令生成1876-1939年的时间虚拟变量，foreach命令为变量treat、count_cl和year_conf生成处理组变量，xtreg命令分别对前述三个变量进行OLS回归。
use "chem_patents_maindataset.dta", clear
forvalues x=1876/1939 {
gen td_`x'=0
qui replace td_`x'=1 if grn==`x'
}
foreach var in treat count_cl year_conf {
forvalues x=1919/1939 {
cap gen `var'_`x'=`var' if grn==`x'
qui replace `var'_`x'=0 if grn!=`x'
}
}
xtreg count_usa treat_* count_for td*, fe i(class_id) robust cluster(class_id)
xtreg count_usa count_cl_1919-count_cl_1939 count_for td*, fe i(class_id) robust cluster(class_id)
xtreg count_usa year_conf_1919-year_conf_1939 count_for td*, fe i(class_id) robust cluster(class_id)
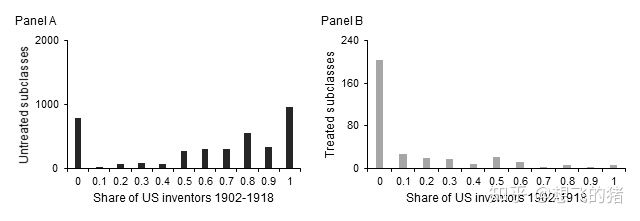
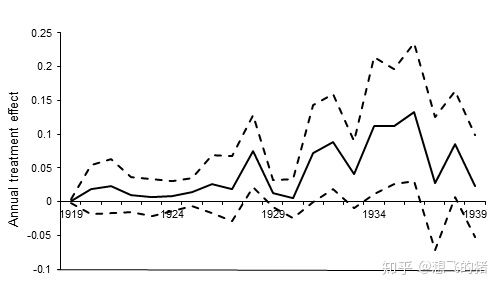
整理命令运行结果，可在Office中绘制图六至八。图形结果显示，全部的强制许可效应从1931年开始有显著上升，说明了专利申请的大量增加开始于1929年，距强制许可集中事实的1919-1922年有6-9年的时滞；1930年代，强制许可效应仍然明显且显著。在控制了专利授权数量和剩余有效年限后，全部的强制许可效应也在1930年之后形成，尽管1927年时，强制许可效应已经在统计上显著了。
3. 三重差分和反事实检验
一些不可观测的因素——例如，德国竞争者在1914-1920年间离开美国市场——会导致双重差分估计量不是一致的估计量。为了解决这个问题，文章采用如下的三重差分模型，在双重差分模型的基础上，再减去不可观测因素对美国专利数量和其他所有非德国专利数量的影响后，可以得到不受不可观测因素影响的强制许可效应。
运行如下命令，可得到三重差分回归结果。在Office中可绘制图九。
use "fig10.dta", clear
xtreg y usa_treat_td1919-usa_treat_td1939 usa_td* usa_treat treat_td* usa td_*, fe i(class_id) robust cluster(class_id)回归结果显示，在TWEA实施以后，处理组的国内专利数量比非德国家的专利数量平均每年多出0.087项；且强制许可效应从1933年起实现，与前文时滞效应结果相吻合。
此外，也可以使用反事实分析来排除不可观测因素的影响。法国的有机化学领域的创新能力在同时期也很落后；但是，法国不受到TWEA条款的影响，而且和美国一样会受到德国在一战期间低效率的影响。
通过估计下述模型，可得到法国在TWEA前后的专利数量的变化。使用下述命令，生成年份虚拟变量和法国专利的处理组、专利数量和剩余有效年限的年份变量后，可以对模型进行回归。根据回归结果，在Office中绘制图十。
use "chem_patents_maindataset.dta", clear
forvalues x=1876/1939 {
gen td_`x'=0
qui replace td_`x'=1 if grn==`x'
}
foreach var in treat count_cl year_conf {
forvalues x=1919/1939 {
cap gen `var'_`x'=`var' if grn==`x'
qui replace `var'_`x'=0 if grn!=`x'
}
}
xtreg count_france treat_* td*, fe i(class_id) robust cluster(class_id)回归结果显示，绝大多数处理效应不显著，因此通过了安慰剂检验。可以认为TWEA只对美国有影响。
4. ITT和IV回归
图五显示，在TWEA颁布前，处理组的美国企业相比对照组有更低的初始技术水平；有理由怀疑处理组的选取不是外生的。为了克服这个问题，可以考虑两种解决办法。一种是ITT（Intent-to-treat）回归，另一种是工具变量（IV）回归。
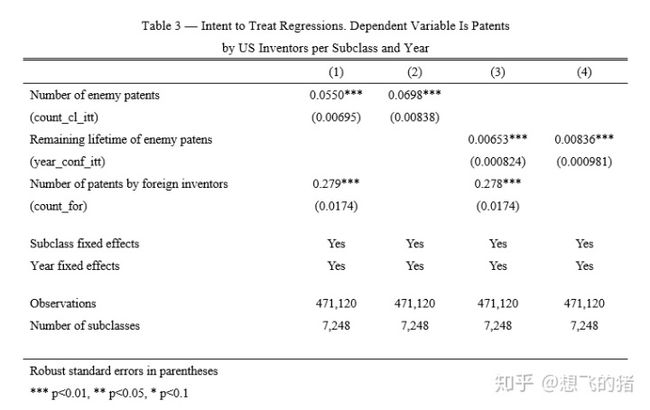
首先，定义ITT为TWEA实施后可利用的外国专利的数量，估计下述模型，可以得到可用的外国专利数量对国内专利数量的影响。运行下述命令，根据回归结果，可绘制表三。
use "chem_patents_maindataset.dta"
forvalues x=1876/1939 {
gen td_`x'=0
qui replace td_`x'=1 if grn==`x'
}
xtreg count_usa count_cl_itt count_for td*, fe i(class_id) robust cluster(class_id)
outreg2 using itt_table3.xls, replace //Table 3, Colume1
xtreg count_usa count_cl_itt td*, fe i(class_id) robust cluster(class_id)
outreg2 using itt_table3.xls, append //Table 3, Colume2
xtreg count_usa year_conf_itt count_for td*, fe i(class_id) robust cluster(class_id)
outreg2 using itt_table3.xls, append //Table 3, Colume3
xtreg count_usa year_conf_itt td*, fe i(class_id) robust cluster(class_id)
outreg2 using itt_table3.xls, append //Table 3, Colume4表三结果显示：可用的外国专利每增加一项，国内专利数量平均每年增加0.055—0.07项；敌方专利的使用年限每增加一年，国内专利数量平均每年增加0.007—0.008项。如果所有的敌方专利以相同概率被强制授权给美国，那么ITT估计量应等于OLS估计量的1/4（336/1377=0.244），但事实上，ITT估计量仅略低于OLS估计量，因而双重差分估计低估了真实的强制许可效应。
其次，可将敌方专利数量作为IV进行两阶段IV回归，因为敌方专利数量与美国专利数量高度相关。根据下述模型进行两阶段IV估计，第一阶段，用工具变量Enemy patents对内生变量专利授权数量回归，第二阶段使用拟合的专利授权数量变量进行OLS回归。
Stata命令如下所示。第一阶段回归分别控制了敌方专利的数量和剩余使用年限，第二阶段回归分别控制了许可专利的数量和剩余使用年限。xtreg命令对第一阶段进行面板回归，xtivreg命令对第二阶段进行面板工具变量回归。
use "chem_patents_maindataset.dta"
forvalues x=1876/1939 {
gen td_`x'=0
qui replace td_`x'=1 if grn==`x'
}
xtreg count_cl count_cl_itt td*, fe i(class_id) robust
outreg2 using iv_table4.xls, replace //Table 4, Colume1
xtreg year_conf year_conf_itt td*, fe i(class_id) robust
outreg2 using iv_table4.xls, append //Table 4, Colume2
xtivreg count_usa (count_cl= count_cl_itt) td*, fe i(class_id)
outreg2 using iv_table4.xls, append //Table 4, Colume3
xtivreg count_usa (year_conf= year_conf_itt) td*, fe i(class_id)
outreg2 using iv_table4.xls, append //Table 4, Colume4表四结果显示：授权的专利每增加一项，国内专利数量平均每年增加0.306项；授权专利的使用年限每增加一年，国内专利数量平均每年增加0.024项。两参数均大于OLS估计量，因而双重差分估计低估了真实的强制许可效应；这也验证了我们之前的结论：美国倾向于将敌方专利授权给初始技术水平较低的企业，因而控制组并不是外生选取的。
四、 稳健性检验
- 控制事前趋势
使用双重差分方法存在的一个严重问题是：处理效应可能是政策和政策发生前处理组与控制组之间已经存在的差异共同造成的。为了解决这个问题，我们构造一个控制了事前时间趋势的DID模型。
其中，δt表示控制了事前时间趋势的年份固定效应，从而，βt+δt表示处理组的强制许可效应，δ表示对照组的时间效应。
运行如下命令，可得到估计结果。根据估计结果，在Office中可绘制图十一。图十一说明，即使在控制了事前时间趋势以后，在TWEA实施期间，处理组的强制许可效应的增加也显著高于对照组。
use "chem_patents_maindataset.dta", clear
forvalues x=1876/1939 {
gen td_`x'=0
qui replace td_`x'=1 if grn==`x'
}
foreach var in treat count_cl year_conf {
forvalues x=1919/1939 {
cap gen `var'_`x'=`var' if grn==`x'
qui replace `var'_`x'=0 if grn!=`x'
}
}
gen trend=licensed_class*grn
xi: xtreg count_usa treat_* td* trend count_for, fe i(class_id) robust cluster(class_id)
另外的事前时间趋势控制方法是，在模型中同时加入子行业层面的时间趋势的一次项和二次项，模型如下所示。该模型的估计结果（未报告）同样显示了处理组效应显著为正。
2. 加入主行业和年份固定效应的交互项
说明事前平行时间趋势的另外一种方法是，在DID模型中加入年份虚拟变量和19个主行业（使用子行业的话，待估参数过多，可能导致模型无法估计）虚拟变量的交互项，模型如下所示。其中，λmt表示USPTO的主行业m和年份t的联合固定效应。
运行下述命令，分别使用处理组、专利许可数量和专利剩余年限对国内发明数量进行回归。根据运行结果，在Office中可绘制表五。回归结果显示，在增加了交互项控制变量后，DID模型估计结果仍然显著且参数值与OLS估计相差不大，因而DID模型估计结果是稳健的。
use "chem_patents_maindataset.dta"
xi: xtreg count_usa treat count_for i.main*i.grn, fe i(class_id) robust cluster(class_id)
outreg2 using table5.xls, replace //Table 5, Colume1
xi: xtreg count_usa count_cl count_for i.main*i.grn, fe i(class_id) robust cluster(class_id)
outreg2 using table5.xls, append //Table 5, Colume2
xi: xtreg count_usa year_conf count_for i.main*i.grn, fe i(class_id) robust cluster(class_id)
outreg2 using table5.xls, append //Table 5, Colume3
3. 删除新创立的子行业和二级子行业
USPTO的行业分类系统存在两个问题：1）USPTO会定期地在系统中添加新的子行业以适应新领域的专利申请；2）USPTO在颁发专利的时候，会将一项专利颁发给不同的二级子行业，从而存在交叉引用技术效应。
对于第一个问题，样本中超过三分之一的子行业是在1919年之后添加进去的，这就会导致DID模型低估了强制许可效应。为解决这一问题，我们将样本限制到子行业c中，并规定c中的子行业在特定年份1919年之前至少产生过一项专利，从而排除了1919年以前不存在的子行业。
通过运行下述命令，可以得到删除新增子行业的回归结果。根据回归结果，在Office中可绘制表六。
use "chem_patents_maindataset.dta"
forvalues x=1876/1939 {
gen td_`x'=0
qui replace td_`x'=1 if grn==`x'
}
sort uspto_class grn //根据uspto_class下的grn进行升序排序
bys uspto: gen ccc=sum(count) //根据uspto_class分类，生成新的变量ccc表示每一子行业的专利数量
foreach var in count_usa count {
qui replace `var'=. if ccc==0
} //如果变量ccc取值为0，说明该子行业无专利存在，那么对应的变量取值为空值
gen aaa=1 if ccc==0 & grn==1919 //生成新的变量aaa，当ccc在1919年时取值为零，则对aaa赋值1
bys uspto: egen bbb=max(aaa) //根据uspto_class分类，生成新的变量bbb，将aaa的最大值赋值给bbb
drop if bbb==1 //删去1919年为止专利数量为0的（新增）子行业
drop if ccc==0 //删去1876-1939年间专利数量为0的子行业
drop aaa bbb ccc //删去变量aaa, bbb ,ccc
xtreg count_usa treat count_for_2 td*, fe i(class_id) robust cluster(class_id)
outreg2 using ols_table6.xls, replace //包含外国专利数量变量滞后两年的回归，结果未汇报
xtreg count_usa treat count_for td*, fe i(class_id) robust cluster(class_id)
outreg2 using ols_table6.xls, append //Table 6, Colume1
xtreg count_usa treat td*, fe i(class_id) robust cluster(class_id)
outreg2 using ols_table6.xls, append //Table 6, Colume2
xtreg count_usa count_cl count_cl_2 count_for td*, fe i(class_id) robust cluster(class_id)
outreg2 using ols_table6.xls, append //Table 6, Colume3
xtreg count_usa count_cl count_for td*, fe i(class_id) robust cluster(class_id)
outreg2 using ols_table6.xls, append //Table 6, Colume4
xtreg count_usa count_cl td*, fe i(class_id) robust cluster(class_id)
outreg2 using ols_table6.xls, append //Table 6, Colume5
xtreg count_usa year_conf year_conf_2 count_for td*, fe i(class_id) robust cluster(class_id)
outreg2 using ols_table6.xls, append //Table 6, Colume6
xtreg count_usa year_conf count_for td*, fe i(class_id) robust cluster(class_id)
outreg2 using ols_table6.xls, append //Table 6, Colume7
xtreg count_usa year_conf td*, fe i(class_id) robust cluster(class_id)
outreg2 using ols_table6.xls, append //Table 6, Colume8
表六与原文献表格略有出入，文献表格未汇报加入外国专利数量滞后两年变量的回归结果，但仅这一回归因为有两年的数据不可用导致样本量减少至221,673个观测值，其余回归的样本观测值均为223,084项。
表六结果说明，删除新产生的子行业样本后，回归结果仍然显著；在TWEA的影响下，处理组的国内发明数量平均每年增加0.142项，是新样本下国内发明数量的16%；类似的，专利许可数量每增加一项，会引起平均每年0.06项国内专利的增加；专利有效年限每增加一年，国内专利数量平均每年增加0.006项。
对于第二个问题， USPTO会将一些子行业同时颁发给不同的子行业，导致这些专利被配置了过高的权重。我们的样本中，有25%的专利被同时颁发给了4个二级子行业。为解决这一问题，现将样本限制在5656个初级子行业中。
通过下述命令，可得到关于5656个初级子行业的回归结果。根据回归结果，可在Office中绘制表七。
use "chem_patents_primaryclassesdataset.dta", clear
forvalues x=1876/1939 {
gen td_`x'=0
qui replace td_`x'=1 if grn==`x'
}
xtreg count_usa treat count_for td*, fe i(class_id) robust cluster(class_id)
outreg2 using ols_table7.xls, replace //Table 7, Colume1
xtreg count_usa count_cl count_for td*, fe i(class_id) robust cluster(class_id)
outreg2 using ols_table7.xls, append //Table 7, Colume2
xtreg count_usa year_conf count_for td*, fe i(class_id) robust cluster(class_id)
outreg2 using ols_table7.xls, append //Table 7, Colume3
表七结果说明，将样本限制在5656个初级子行业后，回归结果仍然显著；在TWEA的影响下，处理组的国内发明数量平均每年增加0.024项（结果不显著），是新样本下国内发明数量的8%；专利许可数量每增加一项，会引起平均每年0.025项国内专利的增加；专利有效年限每增加一年，国内专利数量平均每年增加0.002项。
4. 靛蓝染料行业效应
前文提到过，在1919年TWEA颁布前后，美国国内对很多化工原料的需求很大，因而我们估计出的强制许可效应可能包含着正向的需求冲击导致的国内发明数量增加。为了排除这种需求冲击的影响，本文选取靛蓝染料行业作为样本进行分析；1914年-1921年间，美国的主要染料来源国德国受战争影响，切断了染料供应，导致美国经历了严重的靛蓝染料短缺。因此，除了强制许可效应外，强烈的需求缺口也会促进美国的靛蓝染料的自主发明。
运行下述命令，可得到靛蓝染料的强制许可效应估计结果。根据回归结果，可在Office中绘制图八。图八结果与文献结果有微小出入，主要原因在于数据文件中靛蓝染料行业的样本观测数量为45760个，小于文献中的观测数量46670个。参数结果略有差异，但整体优于原文献回归结果，国外专利数量的参数估计在45760个样本下均为统计显著的。
use "chem_patents_indigodataset.dta", clear
forvalues x=1876/1939 {
gen td_`x'=0
qui replace td_`x'=1 if grn==`x'
}
xtreg count_usa treat count_for td*, fe i(class_id) robust cluster(class_id)
outreg2 using ols_table8.xls, replace //Table 8, Colume1
xtreg count_usa count_cl count_for td*, fe i(class_id) robust cluster(class_id)
outreg2 using ols_table8.xls, append //Table 8, Colume2
xtreg count_usa year_conf count_for td*, fe i(class_id) robust cluster(class_id)
outreg2 using ols_table8.xls, append //Table 8, Colume3
表八的结果同样印证了强制许可能够促进国内创新的结论。在靛蓝染料行业，每增加一项许可专利，处理组的国内专利数量平均每年增加0.0246项，是该行业平均效应水平（0.0435项专利）的56.6%，远高于全行业样本的占比24%。因此，即使在综合了需求冲击的作用时，强制许可效应依旧显著；靛蓝染料行业中的正向需求冲击，强化了强制许可效应，所以其增加的占比远高于全样本的占比。
在回归模型中，允许强制许可效应随时间变化，可以得到动态效应。运行如下命令，可得估计结果。根据回归结果，可在Office绘制图十二。图十二表明，靛蓝染料行业的强制许可效应的时间趋势与全样本下的趋势相似，1931年后出现显著的大幅增加，显著的强制许可效应最早出现在1928年。
use "chem_patents_indigodataset.dta", clear
forvalues x=1876/1939 {
gen td_`x'=0
replace td_`x'=1 if grn==`x'
}
foreach var in treat {
forvalues x=1919/1939 {
cap gen `var'_`x'=`var' if grn==`x'
replace `var'_`x'=0 if grn!=`x'
}
}
xtreg count_us treat_* count_for td*, fe i(class_id) robust cluster(class_id)
五、公司层面的分析
最后，公司层面的分析可以说明强制许可效应促进国内发明数量的作用机制。我们选取杜邦公司作为样本，通过比较特别授权给杜邦公司的专利效应和授权给其他美国公司的专利效应，可以验证20世纪后期形成的“干中学”和“知识溢出”机制，该机制认为，公司内部的学习效应高于公司之间的知识溢出效应。
需估计的模型如下所示，其中，β1表示杜邦公司特有专利的强制许可效应，β2表示授权给其他美国企业的专利的强制许可效应。
运行下述命令，可实现对上述模型的估计。根据回归结果，在Office中绘制表九。
use "dupont_data.dta", clear
xtreg patents treat_NO_dupont treat_dupont count_for td*, fe i(class_id) robust cluster(class_id)
outreg2 using table9.xls, replace //Table 9, Colume1
xtreg patents treat_NO_dupont treat_dupont td*, fe i(class_id) robust cluster(class_id)
outreg2 using table9.xls, append //Table 9, Colume2
xtreg patents count_NO_dupont count_dupont count_for td*, fe i(class_id) robust cluster(class_id)
outreg2 using table9.xls, append //Table 9, Colume3
xtreg patents count_NO_dupont count_dupont td*, fe i(class_id) robust cluster(class_id)
outreg2 using table9.xls, append //Table 9, Colume4
xtreg patents year_conf_NO_dupont year_conf_dupont count_for td*, fe i(class_id) robust cluster(class_id)
outreg2 using table9.xls, append //Table 9, Colume5
xtreg patents year_conf_NO_dupont year_conf_dupont td*, fe i(class_id) robust cluster(class_id)
outreg2 using table9.xls, append //Table 9, Colume6
表九显示，公司独有专利和其他公司拥有的专利均对杜邦公司的专利数量有正向影响。在TWEA的影响下，1919年以后杜邦公司处理组对杜邦公司的发明数量的贡献为，平均每年增加0.094-0.098项；而授权给其他公司的专利子行业，对杜邦公司的发明数量的贡献为平均每年增加0.021-0.025项，约为杜邦公司独有专利子行业影响的三分之一。这说明了，企业内“干中学”效应约为企业间“知识溢出”效应的三倍。
类似的，杜邦公司独有的专利数量每增加一项，带来的杜邦发明数量为平均每年0.051项；而其他公司拥有的专利数量每增加一项，导致杜邦发明数量平均每年增加0.014项，大约为杜邦都有专利影响的四分之一。当回归控制了专利剩余年限时，结论也是如此。
最后，通过下述命令可以估计杜邦公司发明数量的动态时间趋势。根据回归结果，在Office中绘制图十三。图十三结果显示，杜邦公司发明数量的动态时间趋势与全样本趋势类似。
结论
这篇文献使用TWEA作为一项自然实验，检验了强制许可在新兴产业中是否促进了国内发明；结果显示，强制许可对国内发明有较强且持续为正的促进效应。在USPTO分类系统的子行业中，相比控制组，处理组在TWEA的作用下国内专利增加超过20%；在控制了许可专利数量和专利创新程度后，该结果是稳健的。在一系列检验中——例如，比较了美国和其他非德国家的专利数量变化的三重差分（DDD）模型、控制了子行业层面和处理组层面的时间趋势的DD模型、选取法国作为反事实的安慰剂检验等——该结果仍然是稳健的。此外，ITT和IV回归显示，上述分析低估了真实的强制许可效应。
处理效应的分年度估计结果显示，1929年度的强制许可效应最强的，且持续到整个30年代；这也印证了，从获得专利许可到国内的在创新发明之间需要经历一段学习时间。事实上，美国的化工产业确实是在1930年代作为知识原创者而声名鹊起。