4.20天梯模拟赛(并查集,搜索树)
7-7 社交集群 (30 分)
当你在社交网络平台注册时,一般总是被要求填写你的个人兴趣爱好,以便找到具有相同兴趣爱好的潜在的朋友。一个“社交集群”是指部分兴趣爱好相同的人的集合。你需要找出所有的社交集群。
输出格式:
首先在一行中输出不同的社交集群的个数。随后第二行按非增序输出每个集群中的人数。数字间以一个空格分隔,行末不得有多余空格。
输入样例:
8
3: 2 7 10
1: 4
2: 5 3
1: 4
1: 3
1: 4
4: 6 8 1 5
1: 4
输出样例:
3
4 3 1
这道题的爱好是一个可变的集合,我们通过枚举人的爱好更新这个集合并记录这个集合中的人数。通过并查集更新连通块的时候用一个a数组记录每个人的第一个爱好作为标记,相当于这个人最后拿着这个标记作为信号跟有缘人走到一起,形成一个社交集群。
#include7-5 文件传输 (25 分)
这题得了24分,注释的地方写错了,确实写的短就要多注意细节。
#include7-3 朋友圈 (25 分)
某学校有N个学生,形成M个俱乐部。每个俱乐部里的学生有着一定相似的兴趣爱好,形成一个朋友圈。一个学生可以同时属于若干个不同的俱乐部。根据“我的朋友的朋友也是我的朋友”这个推论可以得出,如果A和B是朋友,且B和C是朋友,则A和C也是朋友。请编写程序计算最大朋友圈中有多少人。
输入格式:
输入的第一行包含两个正整数N(≤30000)和M(≤1000),分别代表学校的学生总数和俱乐部的个数。后面的M行每行按以下格式给出1个俱乐部的信息,其中学生从1~N编号:
第i个俱乐部的人数Mi(空格)学生1(空格)学生2 … 学生Mi
输出格式:
输出给出一个整数,表示在最大朋友圈中有多少人。
输入样例:
7 4
3 1 2 3
2 1 4
3 5 6 7
1 6
输出样例:
4
这道题也是并查集,要注意这道题和第一题的cnt初始化是有区别的:
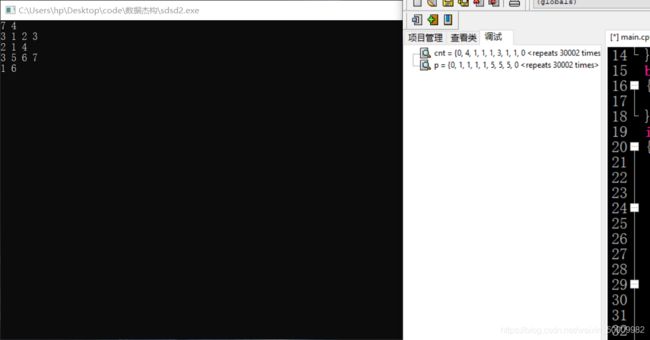
如果对于一个人 4 他没有兴趣爱好:
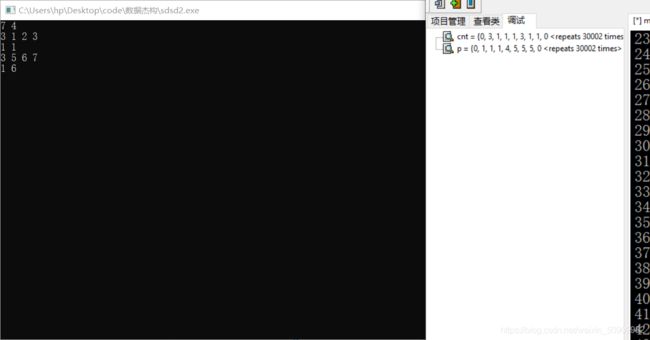
那么他的p[i]=i且,cnt[i]=1的数据我们无法判断他是有一个仅有4的连通块,还是没有这个连通块。
所以如果这道题像第一个题一样要求把每个连通块内部元素个数排序的话,需要再开一个vis数组记录出现过的人,只有一个人出现过,且p[i] = i,且 cnt[i] =1 我们才能认为他是一个孤立点组成的连通块。
#include 7-4 部落 (25 分)
在一个社区里,每个人都有自己的小圈子,还可能同时属于很多不同的朋友圈。我们认为朋友的朋友都算在一个部落里,于是要请你统计一下,在一个给定社区中,到底有多少个互不相交的部落?并且检查任意两个人是否属于同一个部落。
输入格式:
输入在第一行给出一个正整数N(≤10^4 ),是已知小圈子的个数。随后N行,每行按下列格式给出一个小圈子里的人:
K P[1] P[2] ⋯ P[K]
其中K是小圈子里的人数,P[i](i=1,⋯,K)是小圈子里每个人的编号。这里所有人的编号从1开始连续编号,最大编号不会超过10^4。
之后一行给出一个非负整数Q(≤10^4 ),是查询次数。随后Q行,每行给出一对被查询的人的编号。
输出格式:
首先在一行中输出这个社区的总人数、以及互不相交的部落的个数。随后对每一次查询,如果他们属于同一个部落,则在一行中输出Y,否则输出N。
输入样例:
4
3 10 1 2
2 3 4
4 1 5 7 8
3 9 6 4
2
10 5
3 7
输出样例:
10 2
Y
N
简单并查集的应用
这道题我改了一个世纪都不知道自己哪错了,最后发现一个事情:
如果最开始初始化p的范围等于const int N 的这个数,这个题就给我1分,只要让这俩数不相等马上就AC了,不知道这道题是不是编译器的问题,真是吐了。


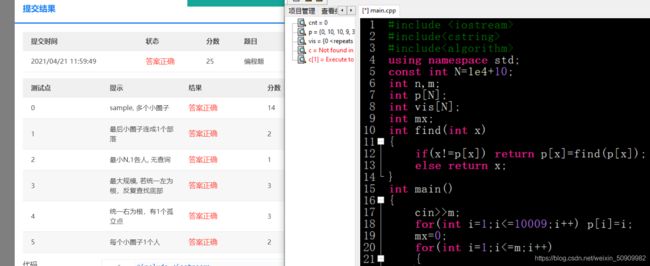
真的无语!
#include 7-8 是否同一棵二叉搜索树 (25 分)
给定一个插入序列就可以唯一确定一棵二叉搜索树。然而,一棵给定的二叉搜索树却可以由多种不同的插入序列得到。例如分别按照序列{2, 1, 3}和{2, 3, 1}插入初始为空的二叉搜索树,都得到一样的结果。于是对于输入的各种插入序列,你需要判断它们是否能生成一样的二叉搜索树。
输入格式:
输入包含若干组测试数据。每组数据的第1行给出两个正整数N (≤10)和L,分别是每个序列插入元素的个数和需要检查的序列个数。第2行给出N个以空格分隔的正整数,作为初始插入序列。最后L行,每行给出N个插入的元素,属于L个需要检查的序列。
简单起见,我们保证每个插入序列都是1到N的一个排列。当读到N为0时,标志输入结束,这组数据不要处理。
输出格式:
对每一组需要检查的序列,如果其生成的二叉搜索树跟对应的初始序列生成的一样,输出“Yes”,否则输出“No”。
输入样例:
4 2
3 1 4 2
3 4 1 2
3 2 4 1
2 1
2 1
1 2
0
输出样例:
Yes
No
No
思路:分别建二叉排序树,然后进行递归比较。
#include排序二叉树的板子也可以短一些:
node *build (node *root,int x)
{
if(root==NULL)
{
root=new node;
root->data=x;
root->lc=root->rc=NULL;
return root;
}
else
{
if(x<root->data)
root->lc=build(root->lc,x);
else
root->rc=build(root->rc,x);
}
return root;
}
7-10 搜索树判断 (25 分)
对于二叉搜索树,我们规定任一结点的左子树仅包含严格小于该结点的键值,而其右子树包含大于或等于该结点的键值。如果我们交换每个节点的左子树和右子树,得到的树叫做镜像二叉搜索树。
现在我们给出一个整数键值序列,请编写程序判断该序列是否为某棵二叉搜索树或某镜像二叉搜索树的前序遍历序列,如果是,则输出对应二叉树的后序遍历序列。
输入格式:
输入的第一行包含一个正整数N(≤1000),第二行包含N个整数,为给出的整数键值序列,数字间以空格分隔。
输出格式:
输出的第一行首先给出判断结果,如果输入的序列是某棵二叉搜索树或某镜像二叉搜索树的前序遍历序列,则输出YES,否侧输出NO。如果判断结果是YES,下一行输出对应二叉树的后序遍历序列。数字间以空格分隔,但行尾不能有多余的空格。
输入样例1:
7
8 6 5 7 10 8 11
输出样例1:
YES
5 7 6 8 11 10 8
输入样例2:
7
8 6 8 5 10 9 11
输出样例2:
NO
原文链接
作者代码写的挺清晰的,先求出二叉排序树,然后求出二叉搜索树的前序遍历,并将其存入数组,对于镜像二叉搜索树的前序,只需要把二叉搜索树的根左右变为根右左来遍历,那么就相当于遍历了镜像二叉搜索树,最后把这两个数组与题目数据对比,处理一下后序输出即可。
#include7-9 树种统计 (25 分)
随着卫星成像技术的应用,自然资源研究机构可以识别每一棵树的种类。请编写程序帮助研究人员统计每种树的数量,计算每种树占总数的百分比。
输入格式:
输入首先给出正整数N(≤10^5),随后N行,每行给出卫星观测到的一棵树的种类名称。种类名称由不超过30个英文字母和空格组成(大小写不区分)。
输出格式:
按字典序递增输出各种树的种类名称及其所占总数的百分比,其间以空格分隔,保留小数点后4位。
输入样例:
29
Red Alder
Ash
Aspen
Basswood
Ash
Beech
Yellow Birch
Ash
Cherry
Cottonwood
Ash
Cypress
Red Elm
Gum
Hackberry
White Oak
Hickory
Pecan
Hard Maple
White Oak
Soft Maple
Red Oak
Red Oak
White Oak
Poplan
Sassafras
Sycamore
Black Walnut
Willow
输出样例:
Ash 13.7931%
Aspen 3.4483%
Basswood 3.4483%
Beech 3.4483%
Black Walnut 3.4483%
Cherry 3.4483%
Cottonwood 3.4483%
Cypress 3.4483%
Gum 3.4483%
Hackberry 3.4483%
Hard Maple 3.4483%
Hickory 3.4483%
Pecan 3.4483%
Poplan 3.4483%
Red Alder 3.4483%
Red Elm 3.4483%
Red Oak 6.8966%
Sassafras 3.4483%
Soft Maple 3.4483%
Sycamore 3.4483%
White Oak 10.3448%
Willow 3.4483%
Yellow Birch 3.4483%
思路:对map容器的使用:
#include输出的时候注意int * 1.0 / int 类型 可以转化为double
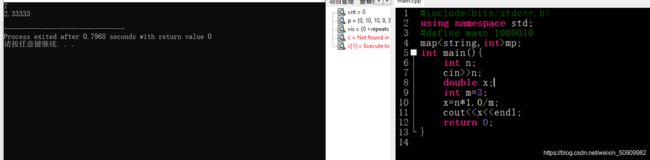
这里区别一下set容器的遍历,输出的是* it:
for(set<string>::iterator it=s.begin();it!=s.end();it++)
cout<<*it<<endl;
