实验一、熟悉MATLAB环境和基本信号的产生与运算

一、实验目的

1.熟悉MATLAB 的运行环境及基本操作命令；
2.掌握MATLAB中信号的表示方法；
3.掌握MATLAB中信号的基本运算；

二、实验器材

计算机、MATLAB软件

三、实验原理

1. MATLAB中信号的表示

在MATLAB中一般用向量来表示信号，由于 MATLAB强大的图形处理功能，为我们实现信号的可视化提供了强有力的工具，所以我们还可以利用MATLAB的绘图命令绘制出直观的信号波形。

（1）连续时间信号

连续时间信号，是指自变量的取值范围是连续的，且对于自变量的一切取值，除了有若干不连续点以外，信号都有确定的值与之对应的信号。从严格意义上来讲，MATLAB并不能处理连续信号，而是用连续信号在等时间间隔点的样值来近似地表示连续信号的，当取样时间间隔足够小时，这些离散的样值就能较好地近似出连续信号。所以，对于连续时间信号，是用两个行向量和来表示，其中向量定义为：，为信号起始时间，为终止时间，为时间间隔。向量为连续信号在向量所定义的时间点上的样值。比如：连续时间信号，可用MATLAB语言表示为：
t=-5:0.1:5; f=cos(t);
用上述向量对连续信号表示后，就可以用plot命令来绘出该信号的时域波形。Plot命令可将点与点间用直线连接，当点与点间的距离很小时，绘出的图形就成了光滑的曲线。命令如下：plot(t,f)，则信号的波形如图1-3所示。

                           图1-3 的波形

（2）离散时间信号

离散时间信号一般用表达式f(k)来表示，其中变量k为整数，代表离散的采样时间点。利用MATLAB表示离散序列f(k)时，也是利用两个向量来表示，其中一个向量表示自变量k的取值范围，另一个向量表示序列f(k)的值。比如序列f(k)={2,2,2,-1,3,0,2;k=-2,-1,0,1,2,3,4}可用MATLAB表示为：
k=-2:4;f=[2,1,2,-1,3,0,2]
此离散时间序列的波形可利用MATLAB函数stem（k，f）画出，如图1-4所示。

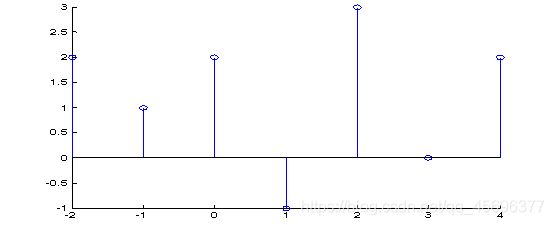
                   图1-4  f(k)的波形图

2．信号的基本运算

信号的基本运算是指信号的加、信号的乘,信号的延迟，翻转等。许多复杂信号就是通过简单信号的基本运算得到的。

（1)信号的加

信号加就是在相同的时间点上将两个或多个信号进行相加。对于连续时间信号，其两个信号的相加可表示为：
y(t)=f1(t)+f2(t)
在MATLAB中，是取连续信号的离散值来进行加的，所以与离散时间信号在MATLAB中的计算方法一样，其MATLAB实现为
y=f1+f2
这就要求f1和f2的长度相同，位置对应，才能进行加法运算，若二者对应变量上的长度不等，则需要根据情况对信号左右补零再进行相加。

（2）信号的乘

信号的乘就是在相同的时间点上将两个或多个信号进行相乘。两个连续时间信号相乘其数学表达式为
y(t)=f1(t)f2(t)
对于离散时间信号，其信号f1(k)和f2(k)相乘是指同一时刻两信号的值对用相乘，可表示为
y(k)=f1(k)f2(k)
其MATLAB实现为
y=f1.*f2
这里也要求两信号的长度必须相等，不等则必须对信号左右补零才能相乘。

（3）信号的翻转

 数学描述              y(k)=x(-k)

其MATLAB实现为
y=fliplr(x)

（4）信号的卷积

在MATLAB中，conv( )函数可以快速求出两个离散时间信号的卷积和。其调用格式为：
y=conv(x,h)
其中调用参数x，h分别为参与卷积运算的两个离散信号，x为包含离散信号的非零样值点的行向量，h为包含离散信号的非零样值点的行向量，向量y则返回离散信号的所有非零样值点行向量。由于conv是MATLAB中针对离散时间信号求卷积的函数，但它不适用于连续时间信号的卷积积分的形式。
例：离散时间信号和的卷积。
程序如下：

      x=[1,2,3,4];
h=[2,1,3];
y=conv(x,h)

运行结果为：

y =
           2     5    11    17    13    12

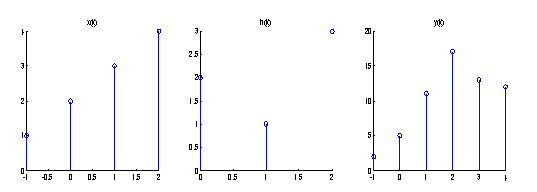
画出信号的波形

subplot(1,3,1);stem(x);title(‘x(k)’);
subplot(1,3,2);stem(h); title(‘h(k)’);
subplot(1,3,3);stem(y); title(‘y(k)’);

其波形如图1-5所示。

            图1-5  离散时间信号卷积和时域波形

由上面例子可以看出，函数conv( )不考虑离散时间信号和的非零样值点的时间序号，也不返回离散时间信号的非零样值点的时间序号。为了完整地表示离散时间信号，我们不仅需要知道卷积的值，还需要知道其值对应的时间序号。由于卷积信号的时域宽带等于和的时域宽带之和减2.其MATLAB生成时间序号的命令如下：

     k1=-1:2
k2=0:2
k=(k1(1)+k2(1)):(k1(end))+k2(length(k2)))

运行结果为
k1 =

              -1     0     1     2

k2 =

               0     1     2

k =

              -1     0     1     2     3     4

根据上面分析，则离散时间信号、以及他们的卷积信号的时域波形如图1-6所示。

             图1-6  离散时间信号卷积和时域波形

（5）序列的相关

利用MATLAB函数conv计算连续时间信号的相关。自相关和互相关序列可以直接调用MATLAB函数xcorr来计算。

（6）常用函数

MATLAB为用户提供了能够产生基本矩阵的几个重要的函数如下：

• zeros：生成零矩阵。调用格式：zeros（n）或者zeros（4，3）
• ones：生成全部元素均为1的矩阵。调用格式：ones（n）或者ones（4，3）
• eye：生成单位矩阵。调用格式：eye（n）或者eye（4，3）
• rand：生成在[0，1]上均匀分布的随机矩阵。调用格式：rand（n）或rand（4，3）
• randn：生成均值为0，方差为1的正态分布的随机矩阵。
• exp:指数函数。
• sin：正弦函数。调用格式：sin（t）
• cos：余弦函数
• rectpule:矩形脉冲信号。调用格式：rectpule(t)或 rectpule(t,w)
• square：生成方波函数。调用格式：square (w0t)或 square (w0t,DUTY)
• sawtooth：生成三角波（锯齿波）。

四、示例演示

1.基本信号波形的可视化

利用MATLAB软件的信号处理工具箱(Signal Processing Toolbox)中的专用函数产生信号并绘出波形。

（1）正弦波和余弦波

程序如下：

t=0:0.01:3*pi;
y1=sin(2*t);
y2=cos(2*t); 
plot(t,y1,t,y2);
legend('正弦波','余弦波');

（2）产生Sinc函数

t=linspace(-5,5,1024);  %t取值的范围
f=sinc(t/pi);        %产生sinc函数
plot(t,f)

（3）产生指数函数波形

x=-2:0.5:2;
y=exp(-x);
plot(x,y);      %连续指数函数
hold on;
stem(x,y);      %离散指数序列

（4）单位阶跃信号

    t=-10:10;
x=((t-0)>=0);
stem(t,x);      %单位阶跃序列
hold on;
plot(t,x,’r’);   %单位阶跃函数

（5）单位冲激序列

    k=-10:10
x=(k==0); 
t=-10:0.01:10;
x1=(t==0);
stem(k,x);     %单位冲激序列
hold on;
plot(t,x1,'r') %单位冲激函数

（6）指数序列

  clear all
a=input('输入指数a= ');
K=input('输入常数K= ');
N=input('输入序列长度N= ');
k=0:N;
x=K*a.^k;
stem(k,x);

（7） 产生高度为1，宽度为4，延时2s的矩形脉冲信号

t=-2:0.02:6;
x=rectpuls(t);
plot(t,x);
axis([-2 6 -0.1 1.1])

（8） 产生幅度为1，基频为2Hz，占空比为50%的周期方波信号

clear all
f0=2;
t=0:0.0001:3;
w0=2*pi*f0;
x=square(w0*t,50);
plot(t,x);
axis([0 3 -1.5 1.5]);

2.信号的运算

（1）两个序列的加、乘运算

clear all
t=0:0.01:2;
f1=2.^(-3*t);
f2=0.7*sin(4*pi*t);
f3=f1+f2;
f4=f1.*f2;
subplot(2,2,1);plot(t,f1);title('f1(t)');grid on;
subplot(2,2,2);plot(t,f2);title('f2(t)');grid on;
subplot(2,2,3);plot(t,f3);title('f1+f2'); grid on;
subplot(2,2,4);plot(t,f4);title('f1*f2'); grid on;

其运行结果如图1-7所示

						图1-7  信号的基本运算

（2）两个序列的相关

利用MATLAB计算两个有限长序列
x[k]=[1,2,-2,1,2,-1,4,4,2],y[k]=[2,-1,4,1,-2,3]的互相关。
程序如下：

x = input('Type in the reference sequence = ');
y = input('Type in the second sequence = ');
% Compute the correlation sequence
n1 = length(y)-1; n2 = length(x)-1;
r = conv(x,fliplr(y));
k = (-n1):n2';
stem(k,r);
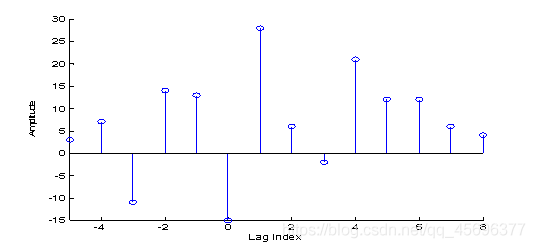
xlabel('Lag index'); ylabel('Amplitude');
v = axis;
axis([-n1 n2 v(3:end)]);

自相关和互相关序列可以直接调用MATLAB函数xcorr来计算。

x = input('Type in the reference sequence = ');
y = input('Type in the second sequence = ');
% Compute the correlation sequence
n1 = length(y)-1; n2 = length(x)-1;
r = xcorr(x,y);
k = (-n1):n2';
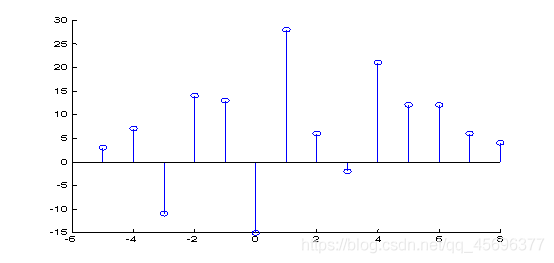
stem(k,r(3:end));
xlabel('Lag index'); ylabel('Amplitude');

五、实验内容

1.了解所给的MATLAB相关函数， 并在计算机上运行这些范例程序,观察其运行结果。并结合范例程序所完成的工作，进一步分析程序中各个语句的作用，从而真正理解这些程序的编程算法。
2.利用MATLAB产生下列信号波形图。
（1）

（2），设

（3），其中，，。

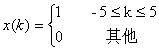
3.已知序列和

（1）计算离散序列的卷积，并绘制其波形图。

（2）计算离散序列的互相关，并绘制其波形图。