Python计算机视觉——图像处理基础章节内容2（作业一）

---

内容介绍

  上一篇博客学习使用了opencv库函数来绘制直方图，实现直方图均衡化和高斯滤波，这次将学习使用PIL、Matplotlib、NumPy等函数库。

  主要是学习使用图像处理的基础操作，包括对图像直方图、高斯滤波、直方图均衡化的实现结果及基本原理。

---

上一篇博客连接：图像处理基础章节内容——opencv库
学习链接: Python计算机视觉编程

---

1. 运行环境：python3.8
2. 编译软件：PyCharm Community 2020.3.3
3. 使用了 Anaconda (开源的Python发行版本)

---

Python对图像处理的基础运用

一、直方图绘制

1、基本原理

  图像处理中，图像直方图是描述图像中该灰度级的像素个数(出现频率)，其中，横坐标表示灰度级，纵坐标表示图像中该灰度级出现的个数(频率)。反映了图像中的灰度分布规律。

2、python实现

python代码：

from PIL import Image
from pylab import *

# 解决中文乱码
plt.rcParams['font.sans-serif'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = False

# 读取图片, PIL库中 Image.open() 函数用于读取图片
# 但是 Image.open() 函数只是保持了图像被读取的状态，图像的真实数据并未被读取
# 因此 使用 array() 函数，将图像打开后，转化为数字矩阵
# 这是 Image.open() 和 opencv 中的 imread() 函数的区别之一，imread() 函数可以读取到图像数据
img = array(Image.open('../image/nuo.jpg'))

figure()
gray()
# axis('off') 展示图片时，不展示坐标轴
axis('off')
imshow(img)
title(u'原图')

figure()
# flatten()函数 将一个数组降到一维，返回一个一维数组
# hist() 函数能够绘制直方图，但是传给的数据要是一维的，所以需要使用 flatten() 函数
hist(img.flatten(), 256)
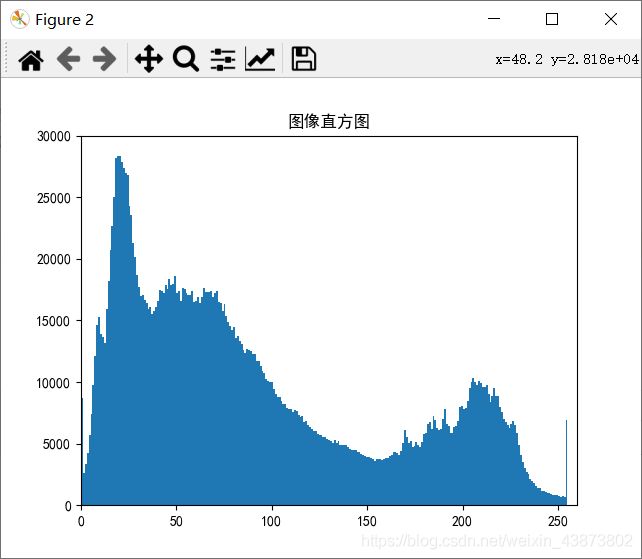
title(u'图像直方图')
plt.xlim([0,260])
plt.ylim([0,30000])

show()

运行结果：

---

二、直方图均衡化

1、基本原理

  直方图均衡化是将原始图片中比较集中的灰度区间变成全部灰度区间的均匀分布。实质上是对图像进行非线性拉伸,重新分配图像象元值,使一定灰度范围内象元值的数量大致相等。从直方图上看，均衡化后的图片的直方图灰度值出现的频率更加均匀。

  在opencv库中，可以使用均衡化函数 equalizeHist() 对图像进行均衡化，而在PCV库中，则使用 histeq() 均衡化函数。

2、python实现

python代码：

from PIL import Image
from pylab import *
from PCV.tools import imtools

# 添加中文字体支持
from matplotlib.font_manager import FontProperties
font = FontProperties(fname=r"c:\windows\fonts\SimSun.ttc", size=14)

# convert()是图像实例对象的一个方法，接受一个 mode 参数，用以指定一种色彩模式
# 1 ------------------（1位像素，黑白，每字节一个像素存储）
# L ------------------（8位像素，黑白）
# P ------------------（8位像素，使用调色板映射到任何其他模式）
# RGB------------------（3x8位像素，真彩色）
# RGBA------------------（4x8位像素，带透明度掩模的真彩色）
# CMYK--------------------（4x8位像素，分色）
# YCbCr--------------------（3x8位像素，彩色视频格式）
# I-----------------------（32位有符号整数像素）
# F------------------------（32位浮点像素）
img = array(Image.open('../image/q.jpg').convert('L'))
# PCV库的 histeq() 均衡化函数
img2, cdf = imtools.histeq(img)

figure()
subplot(2, 2, 1)
axis('off')
gray()
title(u'原始图像', fontproperties=font)
imshow(img)

subplot(2, 2, 2)
axis('off')
title(u'直方图均衡化后的图像', fontproperties=font)
imshow(img2)

subplot(2, 2, 3)
title(u'原始直方图', fontproperties=font)
hist(img.flatten(), 256)

subplot(2, 2, 4)
title(u'均衡化后的直方图', fontproperties=font)
hist(img2.flatten(), 256)

show()

运行结果：

  运行结果可以看出，原图像的象元大多集中在[0,100]区间中，经过均衡化后，图片中比较集中的灰度区间变成全部灰度区间的均匀分布，而均衡化后的图像整体也更加亮了一些，但是均衡化后的图像一些细节消失了。

---

三、高斯滤波

1、基本原理

  高斯滤波是一种线性平滑滤波，适用于消除高斯噪声，广泛应用于图像处理的减噪过程。高斯滤波对于抑制服从正态分布的噪声效果非常好，其代价是使图像变得“模糊”。

  高斯滤波是对整幅图像进行加权平均的过程，每一个像素点的值，都由其本身和邻域内的其他像素值经过加权平均后得到。

  在opencv库中，使用了 GaussianBlur() 函数实现高斯滤波，这次使用SciPy模块，它提供了很多有效的常规操作，包括数值综合、最优化、统计、信号处理以及图像处理。

---

2、python实现高斯模糊

python代码：

from PIL import Image
from pylab import *
from scipy.ndimage import filters

# 添加中文字体支持
from matplotlib.font_manager import FontProperties
font = FontProperties(fname=r"c:\windows\fonts\SimSun.ttc", size=14)

# img = array(Image.open('../image/q.jpg').convert('L'))
img = array(Image.open('../image/q.jpg'))

figure()
gray()
axis('off')
subplot(1, 4, 1)
axis('off')
title(u'原图', fontproperties=font)
imshow(img)

# 灰度图像高斯模糊
# for bi, blur in enumerate([2, 5, 10]):
#   img2 = zeros(img.shape)
#   img2 = filters.gaussian_filter(img, blur)
#   img2 = np.uint8(img2)
#   imNum=str(blur)
#   subplot(1, 4, 2 + bi)
#   axis('off')
#   title(u'标准差为'+imNum, fontproperties=font)
#   imshow(img2)

# 如果是彩色图像，则分别对三个通道进行模糊
for bi, blur in enumerate([2, 5, 10]):
    img2 = zeros(img.shape)
    for i in range(3):
    # gaussian_filter() 高斯滤波函数
        img2[:, :, i] = filters.gaussian_filter(img[:, :, i], blur)
    img2 = np.uint8(img2)
    subplot(1, 4, 2 + bi)
    imNum = str(blur)
    axis('off')
    title(u'标准差为' + imNum, fontproperties=font)
    imshow(img2)

show()

运行结果：

运行结果可以看出，标准差越大，高斯模糊效果越明显。

---

3、加入噪点后进行高斯模糊处理

  高斯滤波处理后能降低噪声的影响，因此可以在原图添加噪声点，来进行比较。

在上述的高斯模糊代码中，读取图片代码后，加入下列添加噪声点的代码：

from PIL import Image
from pylab import *
from scipy.ndimage import filters

# 添加中文字体支持
from matplotlib.font_manager import FontProperties
font = FontProperties(fname=r"c:\windows\fonts\SimSun.ttc", size=14)

img = array(Image.open('../image/q.jpg'))

rows, cols, chn = img.shape
# 添加噪声
for i in range(1000):
    x = np.random.randint(0, rows)
    y = np.random.randint(0, cols)
    img[x, y, :] = 255

gray()
axis('off')
axis('off')
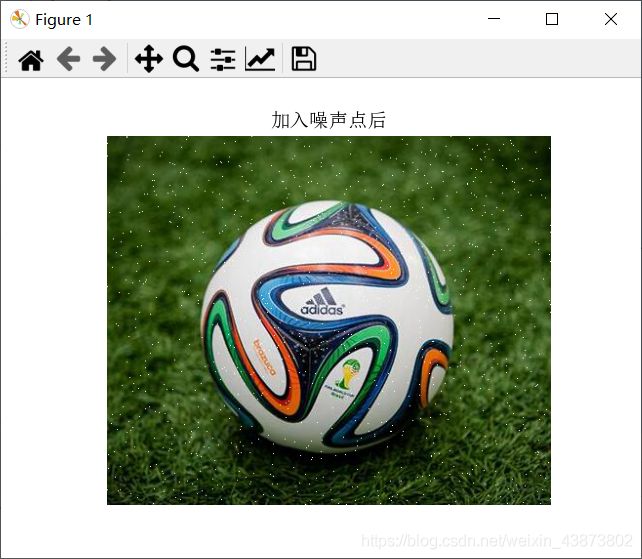
title(u'加入噪声点后', fontproperties=font)
imshow(img)

for bi, blur in enumerate([2, 5, 10]):
    img2 = zeros(img.shape)
    for i in range(3):
        # gaussian_filter() 高斯滤波函数
        img2[:, :, i] = filters.gaussian_filter(img[:, :, i], blur)
    img2 = np.uint8(img2)
    figure()
    gray()
    imNum = str(blur)
    axis('off')
    title(u'标准差为' + imNum, fontproperties=font)
    imshow(img2)

show()

运行结果：

从运行结果可以看出，高斯模糊对于噪声点有明显的抑制效果，其代价是使图像变得“模糊”。