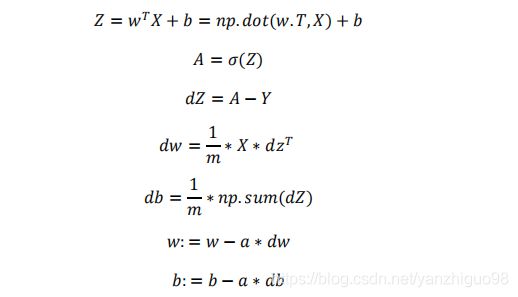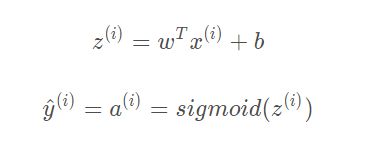深度学习(一)简单神经网络【识别猫】
前一阶段在学习机器学习中的线性回归和logistic回归,学了这些,对于深度学习打下了基础。对于深度学习这一门课,我是在B站上跟着吴恩达老师的课程,再加上黄海广老师整理的深度学习笔记来学习,目前我已经学习完课程一的内容,现在开始做吴恩达老师的实验课。
第一次实验课的内容就是搭建简单的深度学习网络来识别【猫】,我采用的编程环境是pycharm,没有用Jupyter Notebook。我也是在CSDN上参考别人的博客来进行实验的,链接如下:具有神经网络思维的Logistic回归。
一、加载数据与数据预处理
1.1加载数据
具体的数据集来自我上面参考的博客,首先导入数据集,这个很简单,一行代码的事情。
import numpy as np
import pandas as pd
from lr_utils import load_dataset
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
np.set_printoptions(suppress=True)#防止出现科学计数法
train_set_x_orig , train_set_y , test_set_x_orig , test_set_y , classes = load_dataset()1.2查看训练集中的一个图片
#随便查看某一张训练图片
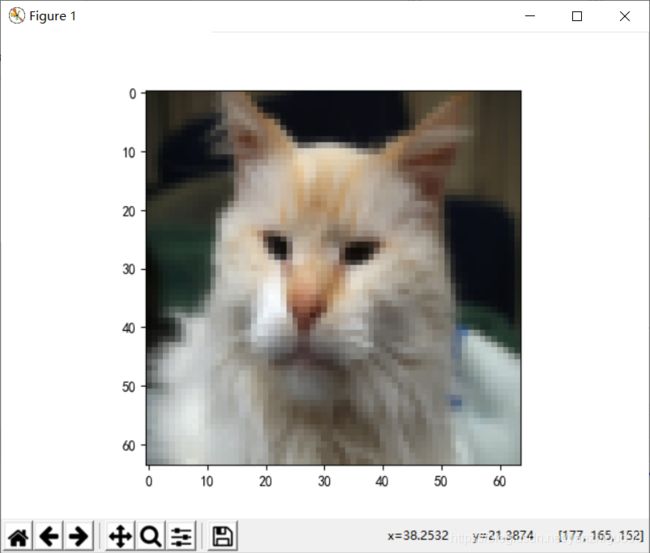
plt.imshow(train_set_x_orig[27])
plt.show()1.3查看训练集和数据的维度
#查看训练集的维度 (209, 64, 64, 3) 一共209张图片 像素是64*64 通道数是3
print(train_set_x_orig.shape)
#查看训练集的维度 (50, 64, 64, 3) 一共50张图片 像素是64*64 通道数是3
print(test_set_x_orig.shape)1.4转化训练集x和测试集x为(n*m)
n*m代表n个特征*m个样本数量
这个是非常重要的,在吴老师的视频中,这个矩阵是作为初始值出入到模型中的。
#将训练集和测试集转换成flatten模式 变更成(64*64*3,m)
train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0],-1).T
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0],-1).T1.5对训练集x和测试集x进行归一化处理
对于我,是个容易忘记的知识点。
归一化处理是为了加速训练神经网络,它一般有两个步骤,首先是零均值,所有数据减去数据的平均值,然后是归一化方差,在第一步后,除以原数据的方差。因为像素值都在0-255之间,所以在这个实验中只需要将所有数据除以255,即可得到均值化结果。
到这,就把所有数据预处理的工作完成了 train_set_x train_set_y test_set_x test_set_y
二、建立神经网络的步骤
2.1定义模型结构(例如输入特征的数量):
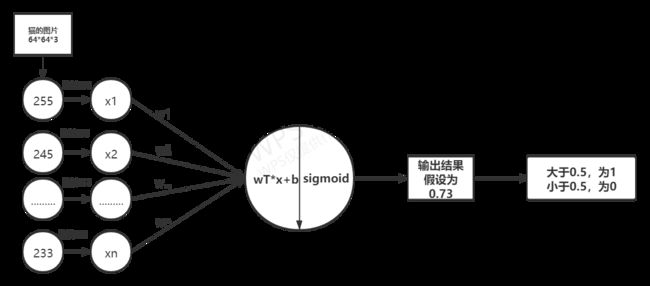
一开始,自己看的太快了,没弄明白这个神经网络的模型,这个神经网络模型只有一个输入层和一个输入层,没有隐藏层。
自己画了一张图:
最好自己在推导一遍公式然后再照着吴老师的代码自己敲一遍,刚开始还是模仿着来吧,毕竟自己不是大佬,不可能一下就写出来。
对于参数的维数的理解:
X:n*m 每个样本中有n个特征 一共有m个样本 对于本例来说 训练集X为12288*209
W:首先设定W一定为(dim,1),因为有12288个特征,所以,W的维数是12288*1
b:因为是单层网络,所以就是一个数字b
Z:因为Z = WT*X+b 结果是(1,209)
Y:根据产生数据集的结果,也是(1,209)
dw:和W维度一致(12288,1)
db:和db维度一致 单个数值
整个向量表达式:
可能是我太笨了,慢慢在纸上推导,才理解这些表达式,过两天又该忘了。。。
2.2定义sigmoid函数
2.3初始化模型的参数:定义参数w和b
2.4定义正向传播和反向传播的函数
2.5循环:
2.5.1计算当前损失(正向传播)
2.5.2计算当前梯度(反向传播)
2.5.3 更新参数(梯度下降)
三、sigmoid函数
除了输入层的每一个神经元都要做两步运算
所以要定义一个sigmoid函数
def sigmoid(x):
'''
计算sigmoid函数值
:param x: w与特征x的乘积
:return:
'''
return 1/(1+np.exp(-x))四、初始化w和b
def initialize_with_zeros(dim):
'''
为w创建一个(dim,1)的向量 b为数字0
:param dim: w的维数
:return:
w
b
'''
w = np.zeros((dim,1))
b = 0
return w,b五、计算成本函数
每一次迭代都要计算正向传播和反向传播,并且要保存每一次迭代之后的成本cost
def propagate(w,b,X,Y):
'''
计算cost function 和正向传播
:param w: 权重矩阵
:param b:偏差
:param X:训练集 n*m
:param Y:真实值 1*m
:return:
cost:代价函数的值
dw:dj/dw的导数
db:dj/db的导数
'''
m = X.shape[1]
A = sigmoid(np.dot(w.T,X)+b)
first = -Y*np.log(A)
second = (1-Y)*np.log(1-A)
cost = np.sum(first-second)/m
dw = (1/m)*np.dot(X,(A-Y).T)
db = (1/m)*np.sum(A-Y)
cost = np.squeeze(cost)
grads = {
"dw":dw,
'db':db
}
return grads,cost六、迭代使得最小化代价函数
def optimize(w,b,X,Y,num_iterations,learning_rate,print_cost=False):
'''
优化w和b
:param w: 权重
:param b: 偏差
:param X: 特征矩阵
:param Y:真实值矩阵
:param num_iterations:迭代次数
:param learning_rate:学习率
:param print_cost:是否打印cost
:return:
params:包含 w和b的字典
grads:包含dw和db的字典
'''
costs=[]
for i in range(num_iterations):
grads,cost = propagate(w,b,X,Y)
dw = grads['dw']
db = grads['db']
w = w - learning_rate*dw
b = b - learning_rate*db
if(i%100==0):
costs.append(cost)
if(print_cost&(i%100==0)):
print('迭代次数:%i 误差值%f'%(i,cost))
params = {
'w':w,
'b':b
}
grads = {
'dw':dw,
'db':db
}
return params,grads,costs其中params字典,是保存最终迭代的结果;grads,保存最后一次迭代之后的dw和db。
将代码【抄】到这个地方,别人写的代码是真好,自己就是想不到
七、根据上一步迭代好的w和b来预测结果
def predict(w,b,X):
'''
使用logistic预测是0还是1
:param w:(求出好的)权重矩阵
:param b:(求出好的)偏置
:param X:测试集
:return:
Y_prediction:测试集预测y(0|1)
'''
m = X.shape[1]
Y_prediction = np.zeros((1,m))
w = w.reshape(X.shape[0],1)
A = sigmoid(np.dot(w.T,X)+b)
for i in range(A.shape[1]):
Y_prediction[0,i] = 1 if A[0,i]>0.5 else 0
return Y_prediction
我觉得这个函数写麻烦了,可以把循环那一部分用np.where改写
def predict(w,b,X):
'''
使用logistic预测是0还是1
:param w:(求出好的)权重矩阵
:param b:(求出好的)偏置
:param X:测试集
:return:
Y_prediction:测试集预测y(0|1)
'''
m = X.shape[1]
w = w.reshape(X.shape[0],1)
A = sigmoid(np.dot(w.T,X)+b)
Y_prediction = np.where(A > 0.5, 1, 0)
return Y_prediction
八、把上述单一功能整合在一个model中
def model(X_train, Y_train, X_test, Y_test, num_iterations=2000, learning_rate=0.5, print_cost=False):
"""
通过调用之前实现的函数来构建逻辑回归模型
参数:
X_train - numpy的数组,维度为(num_px * num_px * 3,m_train)的训练集
Y_train - numpy的数组,维度为(1,m_train)(矢量)的训练标签集
X_test - numpy的数组,维度为(num_px * num_px * 3,m_test)的测试集
Y_test - numpy的数组,维度为(1,m_test)的(向量)的测试标签集
num_iterations - 表示用于优化参数的迭代次数的超参数
learning_rate - 表示optimize()更新规则中使用的学习速率的超参数
print_cost - 设置为true以每100次迭代打印成本
返回:
d - 包含有关模型信息的字典。
"""
w, b = initialize_with_zeros(X_train.shape[0])
parameters, grads, costs = optimize(w, b, X_train, Y_train, num_iterations, learning_rate, print_cost)
# 从字典“参数”中检索参数w和b
w, b = parameters["w"], parameters["b"]
# 预测测试/训练集的例子
Y_prediction_test = predict(w, b, X_test)
Y_prediction_train = predict(w, b, X_train)
# 打印训练后的准确性
print("训练集准确性:", format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100), "%")
print("测试集准确性:", format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100), "%")
d = {
"costs": costs,
"Y_prediction_test": Y_prediction_test,
"Y_prediciton_train": Y_prediction_train,
"w": w,
"b": b,
"learning_rate": learning_rate,
"num_iterations": num_iterations}
return d
九、测试model
print("====================测试model====================")
d = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 2000, learning_rate = 0.005, print_cost = True)
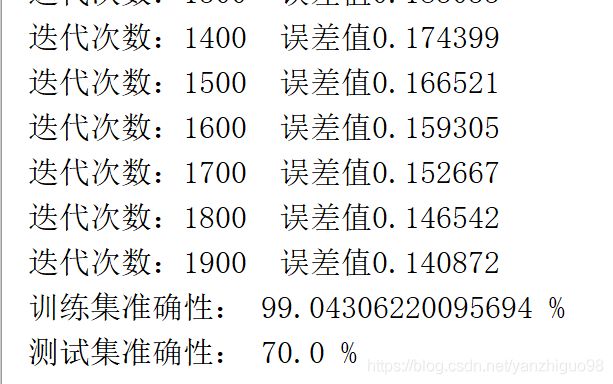
结果图片:
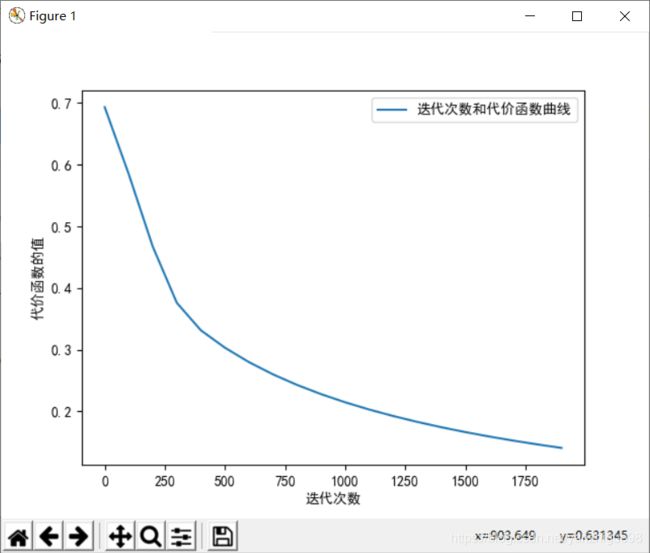
十、迭代次数和学习率关系曲线
d = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 2000, learning_rate = 0.005, print_cost = True)
costs = d['costs']
plt.plot(range(0,2000,100),costs,label = '迭代次数和代价函数曲线')
plt.xlabel('迭代次数')
plt.ylabel('代价函数的值')
plt.legend()
plt.show()
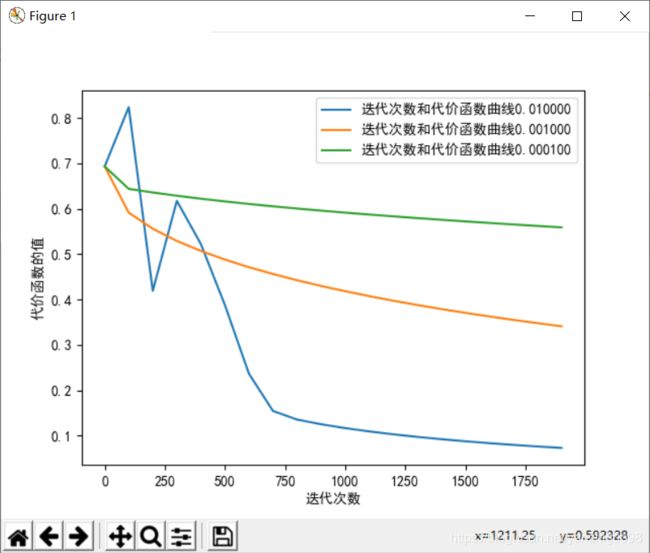
十一、改变学习率观察上述图像
alphas = [0.01,0.001,0.0001]
for i in alphas:
print("使用学习率%f进行迭代"%i)
d = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations=2000, learning_rate=i,
print_cost=True)
costs = d['costs']
plt.plot(range(0, 2000, 100), costs, label='迭代次数和代价函数曲线%f'%i)
plt.xlabel('迭代次数')
plt.ylabel('代价函数的值')
plt.legend()
plt.show()
从上述图像中,可以看出代价函数值最快的的是采用学习率为0.01
运行结果如下:
====================测试model====================
使用学习率0.010000进行迭代
迭代次数:0 误差值0.693147
迭代次数:100 误差值0.823921
迭代次数:200 误差值0.418944
迭代次数:300 误差值0.617350
迭代次数:400 误差值0.522116
迭代次数:500 误差值0.387709
迭代次数:600 误差值0.236254
迭代次数:700 误差值0.154222
迭代次数:800 误差值0.135328
迭代次数:900 误差值0.124971
迭代次数:1000 误差值0.116478
迭代次数:1100 误差值0.109193
迭代次数:1200 误差值0.102804
迭代次数:1300 误差值0.097130
迭代次数:1400 误差值0.092043
迭代次数:1500 误差值0.087453
迭代次数:1600 误差值0.083286
迭代次数:1700 误差值0.079487
迭代次数:1800 误差值0.076007
迭代次数:1900 误差值0.072809
训练集准确性: 99.52153110047847 %
测试集准确性: 70.0 %
使用学习率0.001000进行迭代
迭代次数:0 误差值0.693147
迭代次数:100 误差值0.591289
迭代次数:200 误差值0.555796
迭代次数:300 误差值0.528977
迭代次数:400 误差值0.506881
迭代次数:500 误差值0.487880
迭代次数:600 误差值0.471108
迭代次数:700 误差值0.456046
迭代次数:800 误差值0.442350
迭代次数:900 误差值0.429782
迭代次数:1000 误差值0.418164
迭代次数:1100 误差值0.407362
迭代次数:1200 误差值0.397269
迭代次数:1300 误差值0.387802
迭代次数:1400 误差值0.378888
迭代次数:1500 误差值0.370471
迭代次数:1600 误差值0.362500
迭代次数:1700 误差值0.354934
迭代次数:1800 误差值0.347737
迭代次数:1900 误差值0.340877
训练集准确性: 91.38755980861244 %
测试集准确性: 68.0 %
使用学习率0.000100进行迭代
迭代次数:0 误差值0.693147
迭代次数:100 误差值0.643677
迭代次数:200 误差值0.635737
迭代次数:300 误差值0.628572
迭代次数:400 误差值0.622040
迭代次数:500 误差值0.616029
迭代次数:600 误差值0.610455
迭代次数:700 误差值0.605248
迭代次数:800 误差值0.600354
迭代次数:900 误差值0.595729
迭代次数:1000 误差值0.591339
迭代次数:1100 误差值0.587153
迭代次数:1200 误差值0.583149
迭代次数:1300 误差值0.579307
迭代次数:1400 误差值0.575611
迭代次数:1500 误差值0.572046
迭代次数:1600 误差值0.568601
迭代次数:1700 误差值0.565266
迭代次数:1800 误差值0.562032
迭代次数:1900 误差值0.558891
训练集准确性: 71.29186602870814 %
测试集准确性: 40.0 %可以看出 ,当采用学习率为0.01时,准确性最高,但是测试集准确性只有70%,所以这个模型具有过拟合,只能适用与训练集,不适用与测试集,具体的改进方法在后面的博客中会说到。
十二、附录代码
import numpy as np
import pandas as pd
from lr_utils import load_dataset
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
np.set_printoptions(suppress=True)#防止出现科学计数法
train_set_x_orig , train_set_y , test_set_x_orig , test_set_y , classes = load_dataset()
#随便查看某一张训练图片
# plt.imshow(train_set_x_orig[27])
# plt.show()
#查看训练集的维度 (209, 64, 64, 3) 一共209张图片 像素是64*64 通道数是3
print(train_set_x_orig.shape)
#查看训练集的维度 (50, 64, 64, 3) 一共50张图片 像素是64*64 通道数是3
print(test_set_x_orig.shape)
#m_train 训练集数量 m_test 测试集数量
m_train = train_set_x_orig.shape[0]
m_test = test_set_x_orig.shape[0]
#将训练集和测试集转换成flatten模式 变更成(64*64*3,m)
train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0],-1).T
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0],-1).T
#查看是否正确 结果为(12288,209)
print(train_set_x_flatten.shape)
#归一化操作 因为所有的像素值都在0-255 所以直接除以255即可
train_set_x = train_set_x_flatten/255
test_set_x = test_set_x_flatten/255
#到此就完成了对于样本的处理
# train_set_x
# train_set_y
# test_set_x
# test_set_y
def sigmoid(z):
'''
计算sigmoid函数值
:param z: w与特征x的乘积
:return:sigmoid函数值
'''
return 1/(1+np.exp(-z))
def initialize_with_zeros(dim):
'''
为w创建一个(dim,1)的向量 b为数字0
:param dim: w的维数
:return:
w
b
'''
w = np.zeros((dim,1))
b = 0
return w,b
def propagate(w,b,X,Y):
'''
计算cost function 和正向传播
:param w: 权重矩阵
:param b:偏差
:param X:训练集 n*m
:param Y:真实值 1*m
:return:
cost:代价函数的值
dw:dj/dw的导数
db:dj/db的导数
'''
m = X.shape[1]
A = sigmoid(np.dot(w.T,X)+b)
first = -Y*np.log(A)
second = (1-Y)*np.log(1-A)
cost = np.sum(first-second)/m
dw = (1/m)*np.dot(X,(A-Y).T)
db = (1/m)*np.sum(A-Y)
cost = np.squeeze(cost)
grads = {
"dw":dw,
'db':db
}
return grads,cost
def optimize(w,b,X,Y,num_iterations,learning_rate,print_cost=False):
'''
优化w和b
:param w: 权重
:param b: 偏差
:param X: 特征矩阵
:param Y:真实值矩阵
:param num_iterations:迭代次数
:param learning_rate:学习率
:param print_cost:是否打印cost
:return:
params:包含 w和b的字典
grads:包含dw和db的字典
'''
costs=[]
for i in range(num_iterations):
grads,cost = propagate(w,b,X,Y)
dw = grads['dw']
db = grads['db']
w = w - learning_rate*dw
b = b - learning_rate*db
if(i%100==0):
costs.append(cost)
if(print_cost&(i%100==0)):
print('迭代次数:%i 误差值%f'%(i,cost))
params = {
'w':w,
'b':b
}
grads = {
'dw':dw,
'db':db
}
return params,grads,costs
def predict(w,b,X):
'''
使用logistic预测是0还是1
:param w:(求出好的)权重矩阵
:param b:(求出好的)偏置
:param X:测试集
:return:
Y_prediction:测试集预测y(0|1)
'''
m = X.shape[1]
w = w.reshape(X.shape[0],1)
A = sigmoid(np.dot(w.T,X)+b)
Y_prediction = np.where(A > 0.5, 1, 0)
return Y_prediction
def model(X_train, Y_train, X_test, Y_test, num_iterations=2000, learning_rate=0.5, print_cost=False):
"""
通过调用之前实现的函数来构建逻辑回归模型
参数:
X_train - numpy的数组,维度为(num_px * num_px * 3,m_train)的训练集
Y_train - numpy的数组,维度为(1,m_train)(矢量)的训练标签集
X_test - numpy的数组,维度为(num_px * num_px * 3,m_test)的测试集
Y_test - numpy的数组,维度为(1,m_test)的(向量)的测试标签集
num_iterations - 表示用于优化参数的迭代次数的超参数
learning_rate - 表示optimize()更新规则中使用的学习速率的超参数
print_cost - 设置为true以每100次迭代打印成本
返回:
d - 包含有关模型信息的字典。
"""
w, b = initialize_with_zeros(X_train.shape[0])
parameters, grads, costs = optimize(w, b, X_train, Y_train, num_iterations, learning_rate, print_cost)
# 从字典“参数”中检索参数w和b
w, b = parameters["w"], parameters["b"]
# 预测测试/训练集的例子
Y_prediction_test = predict(w, b, X_test)
Y_prediction_train = predict(w, b, X_train)
# 打印训练后的准确性
print("训练集准确性:", format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100), "%")
print("测试集准确性:", format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100), "%")
d = {
"costs": costs,
"Y_prediction_test": Y_prediction_test,
"Y_prediciton_train": Y_prediction_train,
"w": w,
"b": b,
"learning_rate": learning_rate,
"num_iterations": num_iterations}
return d
print("====================测试model====================")
#这里加载的是真实的数据,请参见上面的代码部分。
alphas = [0.01,0.001,0.0001]
for i in alphas:
print("使用学习率%f进行迭代"%i)
d = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations=2000, learning_rate=i,
print_cost=True)
costs = d['costs']
plt.plot(range(0, 2000, 100), costs, label='迭代次数和代价函数曲线%f'%i)
plt.xlabel('迭代次数')
plt.ylabel('代价函数的值')
plt.legend()
plt.show()
十三、总结
①:熟悉了简单神经网络是如何运行的,但是对于深层的网络又该怎样写代码呢?利用循环去计算每一层的dw和db?又该怎样写呢?自己不知道怎么去做
②:成功复现了吴老师的代码,很高兴
③:理解了那些线代公式的含义,这个才是最重要的!
④:对于一些规律性代码要记住,下次希望自己可以独立写出来,不要再但这篇博客看了。