国王的游戏(华东师范大学-信息学竞赛学教案)
信息学竞赛学教案
【引入问题】:国王的游戏
恰逢H国国庆,国王邀请n位大臣来玩一个有奖游戏。首先,他让每个大臣在左、右手上面分别写下一个整数,国王自己也在左、右手上各写一个整数。然后,让这n位大臣排成一排,国王站在队伍的最前面。排好队后,所有的大臣都会获得国王奖赏的若干金币,每位大臣获得的金币数分别是:排在该大臣前面的所有人的左手上的数的乘积除以他自己右手上的数,然后向下取整得到的结果。国王不希望某一个大臣获得特别多的奖赏,所以他想请你帮他重新安排一下队伍的顺序,使得获得奖赏最多的大臣,所获奖赏尽可能的少。注意,国王的位置始终在队伍的最前面。
【输入】
输入文件为game.in。
第一行包含一个整数n,表示大臣的人数。
第二行包含两个整数a和b,之间用一个空格隔开,分别表示国王左手和右手上的整数。
接下来 n 行,每行包含两个整数 a 和 b,之间用一个空格隔开,分别表示每个大臣左手和右手上的整数。
【输出】
输出文件名为.out。
输出只有一行,包含一个整数,表示重新排列后的队伍中获奖赏最多的大臣所获得的金币数。
【输入输出样例】
Game .in Game .out
3 2
1 1
2 3
7 4
4 6
【输入输出样例说明】
按1、2、3号大臣这样排列队伍,获得奖赏最多的大臣所获得金币数为2;
按1、3、2这样排列队伍,获得奖赏最多的大臣所获得金币数为2;
按2、1、3这样排列队伍,获得奖赏最多的大臣所获得金币数为2;
按2、3、1这样排列队伍,获得奖赏最多的大臣所获得金币数为9;
按3、1、2这样排列队伍,获得奖赏最多的大臣所获得金币数为2;
按3、2、1这样排列队伍,获得奖赏最多的大臣所获得金币数为9。
因此,奖赏最多的大臣最少获得 2 个金币,答案输出 2。
【数据范围】
对于20%的数据,有1≤n≤10,0 < a、b <8;
对于40%的数据,有1≤n≤20,0 < a、b < 8;
对于60%的数据,有1≤n≤100;
对于60%的数据,保证答案不超过109;
对于 100%的数据,有 1 ≤n ≤1,000,0 < a、b < 10000。
【问题分析】:这道题主要关键是与前面的有关,而与后面的无关。我们可以先确定第n个大臣,然后确定第n-1个大臣,依次类推,因为我们确定了第i个大臣后,第1~i-1个大臣都不用乘以i~n个大臣的左手,也就是没有后效性。那么如果第i个大臣是排在最后,那么就要奖赏:left(1,n)/(right(i)*left(i)),我们把每一位大臣的这个值算出来,装在v数组里面,然后按从大到小排序。为什么是从大到小呢,如图所示,数组v,已按从大到小排序,所以v[i]>v[j].
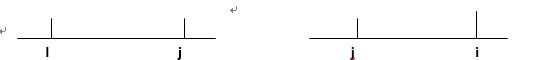
如果i、j的位置不变,那么奖赏最多的大臣有可能在i、j之间,但是如果把i、j的位置转换,我们知道,在v[i]~v[j]之中,v[i]是最大的所以获得最多的奖赏的大臣肯定是i,比之前的更差或不变。所以我们要按从大到小排序,我们发现left(1,n)/(right(i)*left(i))中,left(1,n)是不变的,我们把这个公式*1/(left(1,n)),公式就变成right[i]*left[i],但因为乘了一个倒数,所以符号变了,所以要按 right[i]*left[i] 的值从小到大排序。然后模拟一次就可以了。
因为数很大(对于100%的数据,有1《n《1000, 0<a,b<10000)所以要用高精度乘和高精度除。
由此引出大整数的乘除法:
大整数的乘法:
Int a[1000],b[1000],result[1000]
现在要计算:
a[0]a[1]a[2]a[3]a[4]……a[999]
X b[0]b[1]b[2]b[3]b[4]……b[999]
=?
首先低位对齐,此处设定的是 a[0]为高位,则可能数组 a 并没有存满。
a[0]a[1]a[2]a[3]a[4]……a[i]
X b[j]
Result[n-1]+=a[i]*b[j]%10000
Result[n-2]+= a[i]*b[j]/10000 进位
……
循环
2 大整数的除法:
现在要计算(大整数除以一个简单的整数):
bi )a[0]a[1]a[2]a[3]a[4]……a[999]
判定:a[0]<bi?
Yes: shang[i] = (a[0]*10000+a[1])/bi shang[i+1]=(( a[0]*10000+a[1])%bi)*10000+a[2])/bi
No: shang[i] = a[0]/bi shang[i+1]=((a[0]%bi)*10000+a[1])/bi
循环,注意 a[0]=bi 时候的情况
【引出参考代码】:.python
[n],*k=([int(x) for x in line.split()]for line in open('4302.in'))
c=[[0,0]]*n
for i in range(1,n+1):
c[i-1]=[k[i][0]*k[i][1],i]
c.sort()
king=k[0][0]
MAX=king//k[c[0][1]][1]
for x in range(0,n):
t=king//k[c[x][1]][1]
king=king*k[c[x][1]][0]
if t>MAX:
MAX=t
open('4302.out','w').write('{:d}\n'.format(MAX))
学生提问,是否听懂,以及讲解。
完。