用逆变换采样方法构建随机变量生成器
本公众号MyEncyclopedia定期发布AI,算法,工程类深度和前沿文章。学习本文的最佳姿势为点击文末在看,发送本文链接到桌面版浏览器,打开文末阅读原文,敲入代码运行。
上期 从零构建统计随机变量生成器之离散基础篇,我们从零出发构建了基于伯努利的基础离散分布,这一期我们来详细介绍广泛使用的 Inverse Transform Method(逆变换采样方法)。
逆变换采样方法
Inverse Transform Method 是最基础常见的方法,可用于离散分布和连续分布。常见的分布一般都能通过此方法生成,只需要随机变量CDF的解析表达式。假设随机变量 ,其CDF为 ,则 Inverse Transform Method 仅有两步
通过生成 [0, 1] 之间的均匀随机数
代入 即产生满足 分布的实例
离散例子
我们先举一个离散分布来直观感受一下其工作机制。有如下PMF的离散类别分布,范围在 [1, 5]。
转换成CDF为
画出对应的CDF图
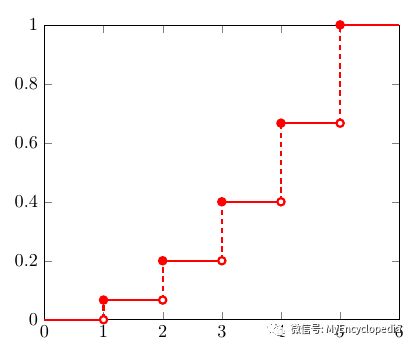
那么Inverse Transformation Method 的第一步,随机生成 0-1 之间的数 u,可以直观的认为是在 y 轴上生成一个随机的点 u。注意到5段竖虚线对应了5个离散的取值,它们的长度和为1,并且每一段长度代表了每个值的权重。因此,通过在 y 轴上的均匀采样可以生成给定PMF的 x 的分布。
离散分布的逆变换采样方法用数学公式可以表述为:找到第一个 x,其CDF的范围包括了 u,即
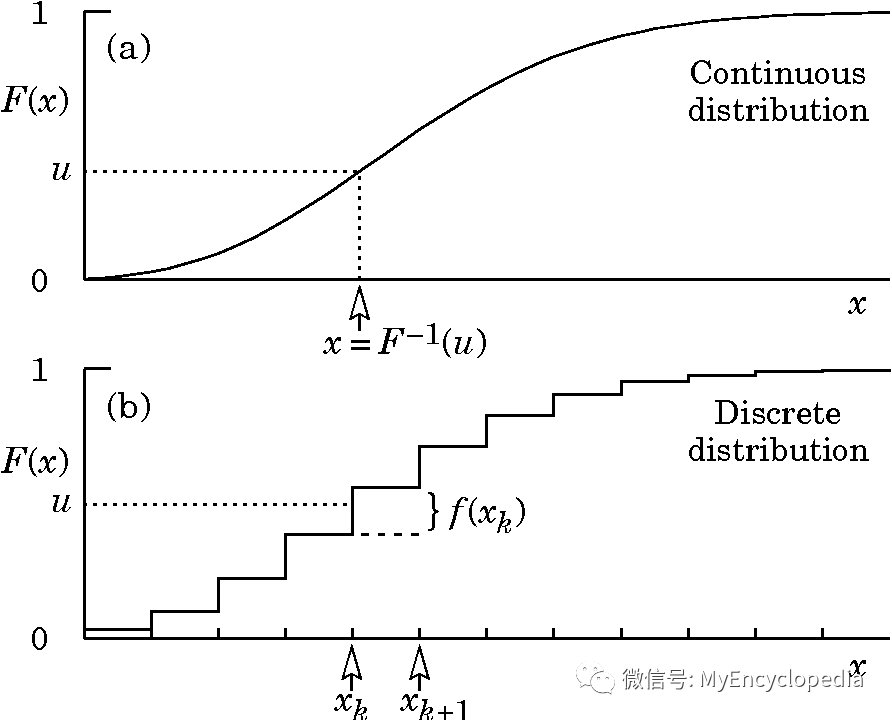
扩展到连续分布
有了离散类别分布的直观感受,扩展到连续分布也就不难理解了。类似于微积分中将连续空间做离散切分,再通过极限的方法,连续光滑函数在 y 轴上可以切分成长度为 的线段,那么生成的 x 值就是其近似值。随着 ,最终 即为满足要求的分布。
指数分布(连续)
以最为常见的指数分布为例,我们来看看具体的步骤。
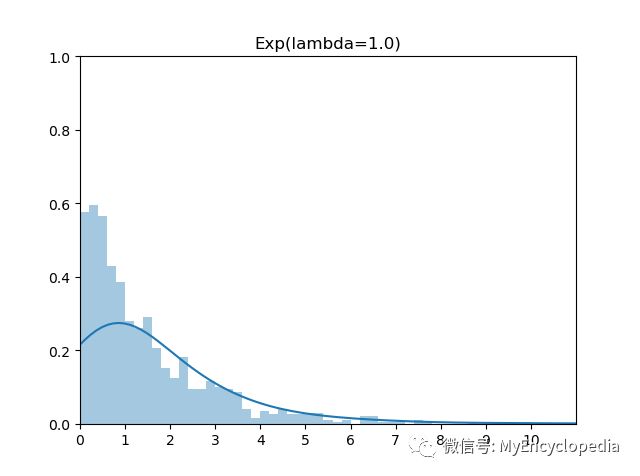
我们知道指数分布的PDF如下
PDF 图为
计算CDF为
CDF 图
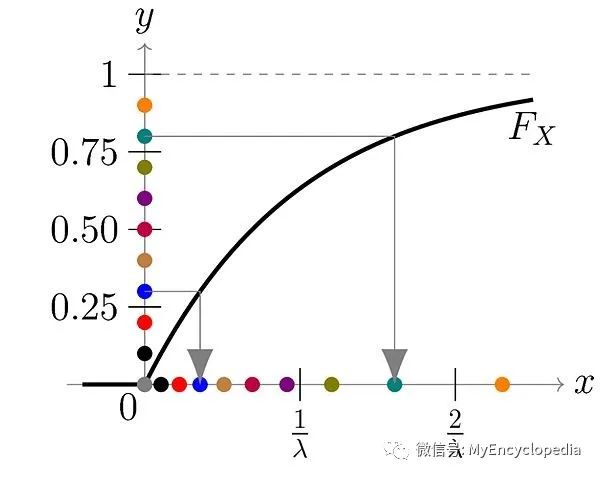
可以求得逆函数为
由于 1-u 在 [0, 1] 范围上的随机数等价于 u,因此,x 的生成公式等价于
实现代码
对应代码很简单
import random
from math import log2 as ln
def exp_gen(lambbda: float) -> float:
u = random.random()
return -ln(u) / lambbda
Github 代码地址:
https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/coutinous_exp_inv.py
持续模拟动画
类别分布(离散)
我们再来看基于类别分布 Inverse Transformation Method的其他离散分布例子。在从零构建统计随机变量生成器之离散基础篇中,我们已经介绍了类别分布(Categorical Distribution)的逆变换采样算法,同时还介绍了通过模拟 Bernoulli 实验来生成二项,几何,超几何分布的方法。在这一篇中,我们通过逆变换采样算法再来生成这些分布。
先回顾一下类别分布的逆变换采样实现。
给定如下的类别分布,
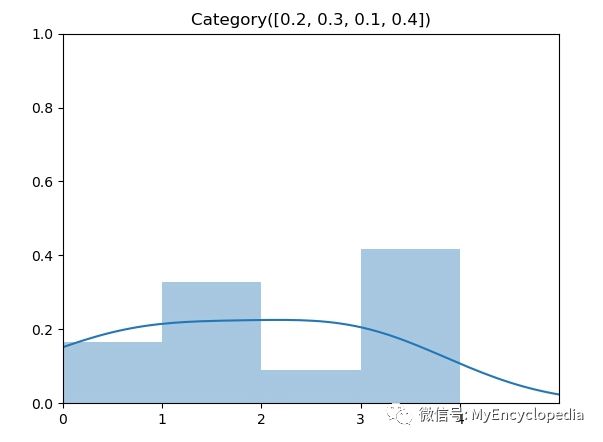
实现代码
类别分布的逆变换采样实现需要找到第一个大于 u 的元素的索引序号,在我们的实现中,将 转换成累计概率 后,由于 数组是非递减的,因此我们可以用二分法代替线性查找,将时间复杂度降到 。下面的实现中直接调用 python bisect 函数即可。
import bisect
import random
from typing import List
def categorical(probs: List[float]) -> int:
assert abs(sum(probs) - 1.0) < 0.001
cum = probs.copy()
for i in range(1, len(cum)):
cum[i] = cum[i-1] + probs[i]
u = random.random()
return bisect.bisect(cum, u)
Github 代码地址:
https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/discrete_categorical.py
二项分布(离散)
二项分布(Binomial Distribution)有两个参数 n 和 p,表示伯努利实验做n次后成功的次数。图中为 n=6,p=0.5的二项分布。
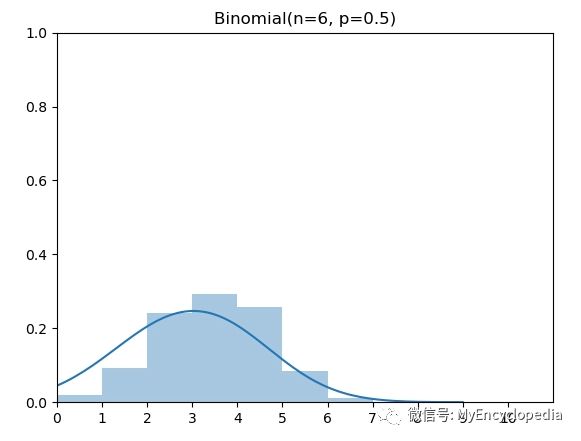
概率质量函数(PMF)
实现代码
根据上面的PMF定义,我们将 [0, 6] 上的PMF计算出来,然后调用类别分布的逆变换采样实现即可:
from scipy.special import comb
from discrete_categorical import categorical
from math import pow
def binomial(n: int, p: float) -> int:
pmf = [comb(n, k, exact=True) * pow(p, k) * pow(1-p, n-k) for k in range(0, n + 1)]
return categorical(pmf)
Github 代码地址:
https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/discrete_binomial_inv.py
持续模拟动画
超几何分布(离散)
同样的,超几何分布(HyperGeometric Distribution)也可以如法炮制。
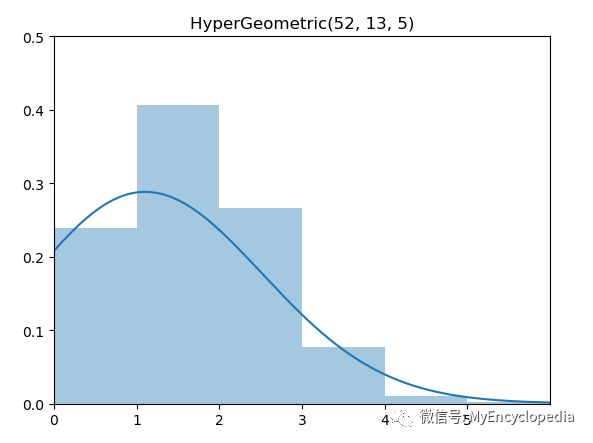
概率质量函数(PMF)
实现代码
from scipy.special import comb
from discrete_categorical import categorical
def hypergeometric(N: int, K_succ_num: int, n_trial_num: int) -> int:
pmf = [comb(K_succ_num, k, exact=True) * comb(N - K_succ_num, n_trial_num - k, exact=True) / comb(N, n_trial_num, exact=True)
for k in range(max(0, n_trial_num - (N - K_succ_num)), min(K_succ_num, n_trial_num) + 1)]
return categorical(pmf)
Github 代码地址:
https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/discrete_hypergeometric_inv.py
持续模拟动画
几何分布(离散)
几何分布(Geometric Distribution)和上面的二项分布以及超几何分布不同的是,它的 support 是所有非负整数,因此,我们无法穷举计算所有 x 的概率。但是,我们可以通过将CDF 推出 Inverse CDF的解析表达式来直接实现。
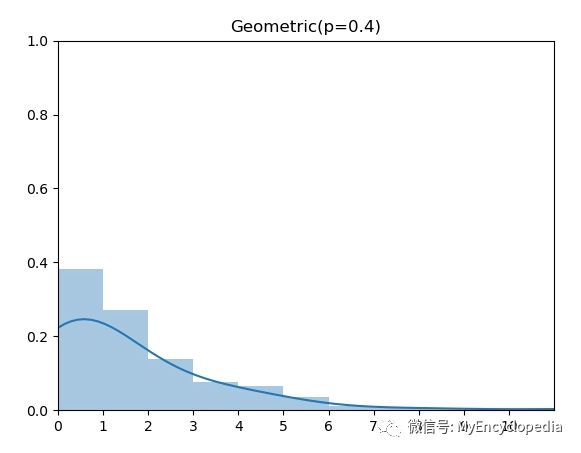
概率质量函数(PMF)
CDF
Inverse CDF
反函数求得为
实现代码
import random
from math import floor
from math import log2 as ln
def geometric(p: float) -> int:
u = random.random()
return floor(ln(u) / ln(1-p))
Github 代码地址:
https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/discrete_geometric_inv.py
持续模拟动画
标准正态分布
一般,标准正态分布用Box-Muller 方法来生成,这个后续将做详细介绍。这里我们用 Schmeiser 提出的基于Inverse Transformation Method的近似方法来生成:
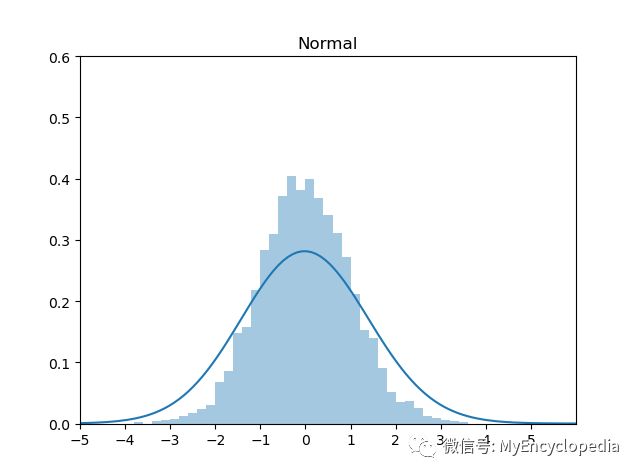
实现代码
import random
def normal():
import math
u = random.random()
return (math.pow(u, 0.135) - math.pow(1-u, 0.135)) / 0.1975
Github 代码地址:
https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/coutinous_normal_apprx.py
持续模拟动画
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。