第十二届蓝桥杯模拟赛Python组（第三期）

第一题

# 问题描述
# 　　请问在 1 到 2020 中，有多少个数与 2020 互质，即有多少个数与 2020 的最大公约数为 1。
# 答案提交
# 　　这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。
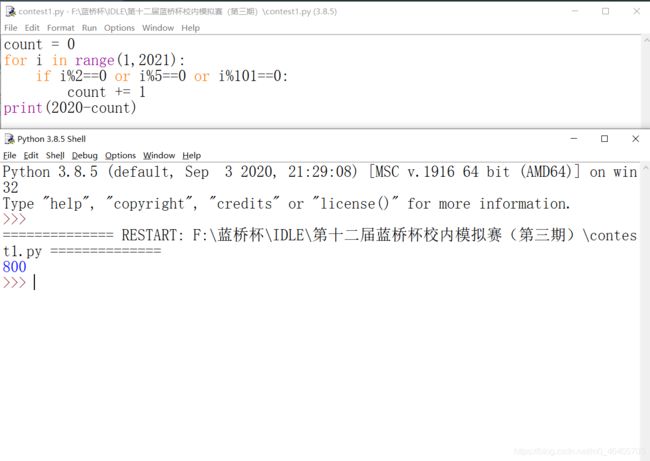
co = 0
for i in range(1,2021):
    if i % 2 == 0 or i % 5 == 0 or i % 101 == 0:
        co += 1
print(2020-co)

答案：800

第二题

# 问题描述
# ASCII 码将每个字符对应到一个数值（编码），用于信息的表示和传输。在 ASCII 码中，英文字母是按从小到大的顺序依次编码的，例如：字母 A 编码是 65, 字母 B 编码是 66，字母 C 编码是 67，请问字母 Q 编码是多少？
# 答案提交
# 　　这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。
print(ord('Q'))
'''
ord() 函数是 chr() 函数（对于8位的ASCII字符串）或 unichr() 函数（对于Unicode对象）的配对函数，
它以一个字符（长度为1的字符串）作为参数，返回对应的 ASCII 数值，或者 Unicode 数值，如果所给的 Unicode 
字符超出了你的 Python 定义范围，则会引发一个 TypeError 的异常。
'''

答案：81

第三题

n2 = 1000
n0 = n2 + 1         # 二叉树最重要的性质
print(n0)

答案：1001

第四题

'''
问题描述
　　对于整数 v 和 p，定义 Pierce 序列为：
　　a[1] = v
　　a[i] = p % a[i-1]
　　例如，当 v = 8, p = 21 时，对应的 Pierce 序列为
　　a[1] = 8
　　a[2] = 5
　　a[3] = 1
　　再往后计算，值变为 0，不在我们考虑的范围内。因此当 v = 8, p = 21 时， Pierce 序列的长度为 3。
　　当 p 一定时，对于不同的 v 值，Pierce 序列的长度可能不同。当 p = 8 时，若 1<=v

def Pierce(p,v):
    a = []
    while v>0:
        for i in range(1,100):
            if i==1:
                a.append(v)
            else:
                if a[i-2]==0:
                    break
                else:
                    a.append(p%a[i-2])
                    v = a[i-1]
    a.pop()
    return a,len(a)
print(Pierce(2021,1160))

答案：12

第五题

# 问题描述
# 　　在 Excel 中，第 1 列到第 26 列的列名依次为 A 到 Z，从第 27 列开始，列名有两个字母组成，第 27 列到第 702 列的列名依次为 AA 到 ZZ。
# 　　之后的列再用 3 个字母、4 个字母表示。
# 　　请问，第 2021 列的列名是什么？
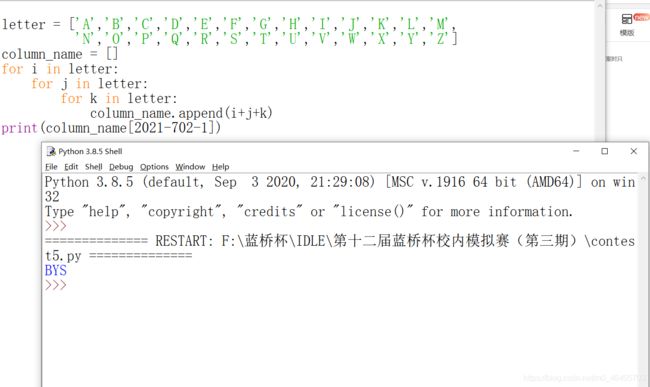
dic = ['A','B','C','D','E','F','G','H','I','J','K','L','M','N','O','P','Q',
       'R','S','T','U','V','W','X','Y','Z']
a = []
for i in dic:
    for j in dic:           # 依次循环迭代
        for v in dic:
            index = i + j + v
            a.append(index)
print(a[2021-702-1])        # 索引从0开始，所以要减一

答案：BYS

第六题

'''
问题描述
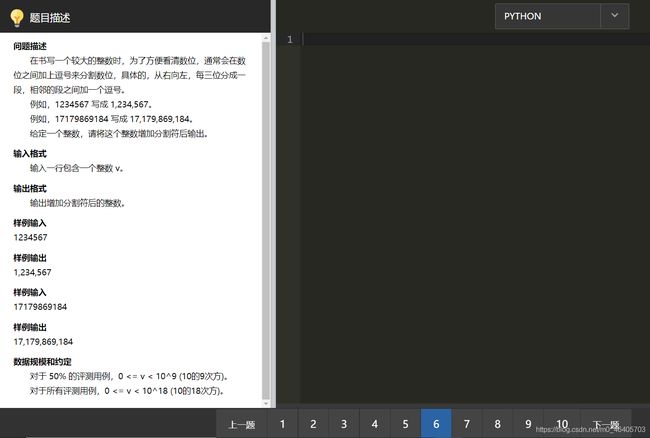
　　在书写一个较大的整数时，为了方便看清数位，通常会在数位之间加上逗号来分割数位，具体的，从右向左，每三位分成一段，相邻的段之间加一个逗号。
　　例如，1234567 写成 1,234,567。
　　例如，17179869184 写成 17,179,869,184。
　　给定一个整数，请将这个整数增加分割符后输出。
输入格式
　　输入一行包含一个整数 v。
输出格式
　　输出增加分割符后的整数。
样例输入
1234567
样例输出
1,234,567
样例输入
17179869184
样例输出
17,179,869,184
数据规模和约定
　　对于 50% 的评测用例，0 <= v < 10^9 (10的9次方)。
　　对于所有评测用例，0 <= v < 10^18 (10的18次方)。
'''
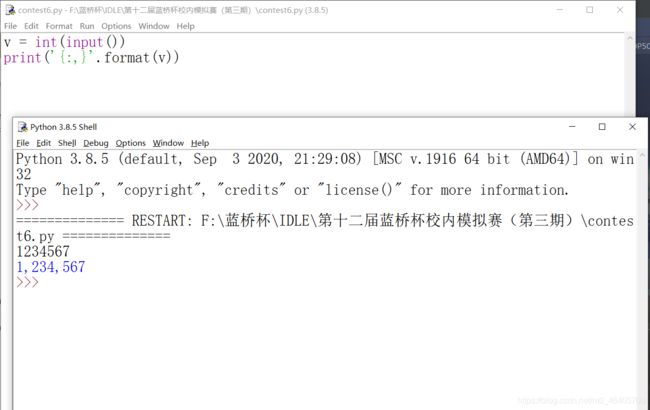
v = int(input())
print('{:,}'.format(v))     # 逗号在这里表示千位分隔符
# 这是刚入门Python学的知识啊，考试的时候竟然没想到

第七题

'''
问题描述
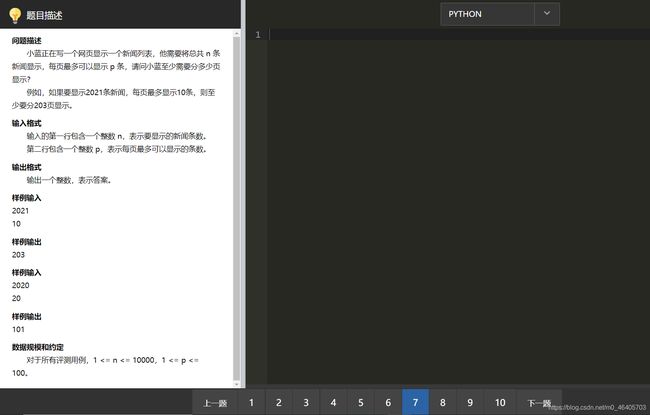
　　小蓝正在写一个网页显示一个新闻列表，他需要将总共 n 条新闻显示，每页最多可以显示 p 条，请问小蓝至少需要分多少页显示？
　　例如，如果要显示2021条新闻，每页最多显示10条，则至少要分203页显示。
输入格式
　　输入的第一行包含一个整数 n，表示要显示的新闻条数。
　　第二行包含一个整数 p，表示每页最多可以显示的条数。
输出格式
　　输出一个整数，表示答案。
样例输入
2021
10
样例输出
203
样例输入
2020
20
样例输出
101
数据规模和约定
　　对于所有评测用例，1 <= n <= 10000，1 <= p <= 100。
'''
n = int(input())    # 新闻条数
p = int(input())    # 显示条数

if n%p == 0:
    count = n/p
else:
    count = n//p + 1
print(int(count))

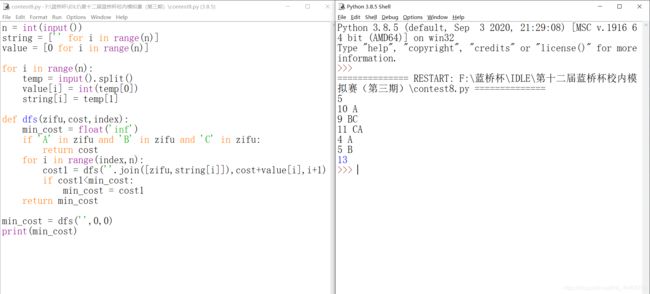
第八题

'''
问题描述
　　杂货铺老板一共有N件物品，每件物品具有ABC三种属性中的一种或多种。从杂货铺老板处购得一件物品需要支付相应的代价。
　　现在你需要计算出如何购买物品，可以使得ABC三种属性中的每一种都在至少一件购买的物品中出现，并且支付的总代价最小。
输入格式
　　输入第一行包含一个整数N。
　　以下N行，每行包含一个整数C和一个只包含"ABC"的字符串，代表购得该物品的代价和其具有的属性。
输出格式
　　输出一个整数，代表最小的代价。如果无论如何凑不齐ABC三种属性，输出-1。
样例输入
5
10 A
9 BC
11 CA
4 A
5 B
样例输出
13
数据规模和约定
　　对于50%的评测用例，1 <= N <= 20
　　对于所有评测用例，1 <= N <= 1000， 1 <= C <= 100000
'''
n = int(input())
string = ['' for i in range(n)]
value = [0 for i in range(n)]

for i in range(n):
    temp = input().split()
    value[i] = int(temp[0])
    string[i] = temp[1]

def dfs(zifu,cost,index):
    min_cost = float('inf')
    if 'A' in zifu and 'B' in zifu and 'C' in zifu:
        return cost
    # if index>n:
    #     return float('inf')
    for i in range(index,n):
        print(''.join([zifu,string[i]]),cost+value[i],i+1)
        cost1 = dfs(''.join([zifu,string[i]]),cost+value[i],i+1)
        if cost1<min_cost:
            min_cost = cost1
    return min_cost

min_cost = dfs('',0,0)
print(min_cost)

第九题

'''
问题描述
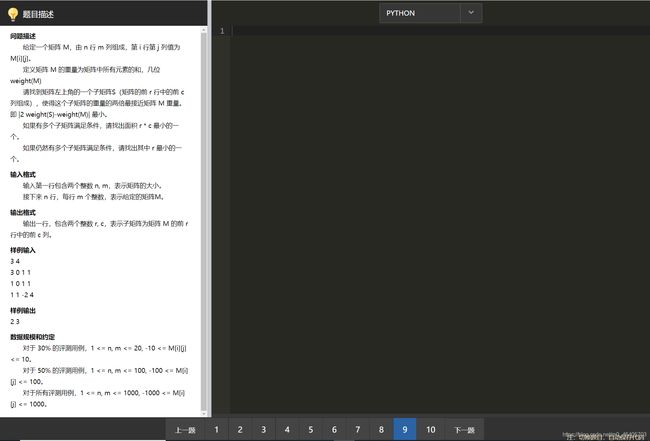
　　给定一个矩阵 M，由 n 行 m 列组成，第 i 行第 j 列值为 M[i][j]。
　　定义矩阵 M 的重量为矩阵中所有元素的和，记为weight(M)
　　请找到矩阵左上角的一个子矩阵S（矩阵的前 r 行中的前 c 列组成），使得这个子矩阵的重量的两倍最接近矩阵 M 重量。即 |2 weight(S)-weight(M)| 最小。
　　如果有多个子矩阵满足条件，请找出面积 r * c 最小的一个。
　　如果仍然有多个子矩阵满足条件，请找出其中 r 最小的一个。
输入格式
　　输入第一行包含两个整数 n, m，表示矩阵的大小。
　　接下来 n 行，每行 m 个整数，表示给定的矩阵M。
输出格式
　　输出一行，包含两个整数 r, c，表示子矩阵为矩阵 M 的前 r 行中的前 c 列。
样例输入
3 4
3 0 1 1
1 0 1 1
1 1 -2 4
样例输出
2 3
数据规模和约定
　　对于 30% 的评测用例，1 <= n, m <= 20, -10 <= M[i][j] <= 10。
　　对于 50% 的评测用例，1 <= n, m <= 100, -100 <= M[i][j] <= 100。
　　对于所有评测用例，1 <= n, m <= 1000, -1000 <= M[i][j] <= 1000。
'''
n,m = map(int,input().split())
dp = [[0]*m for i in range(n+1)]
value = []
weight = 0
for i in range(n):
    value.append(list(map(int,input().split())))
    weight += sum(value[i])
# print(dp)
# print(weight)
answer_value = float("inf")     # 初始化为无穷大
answer_area = float("inf")      # 初始化为正无穷
for r in range(1,n):
    for c in range(1,m):
        dp[r][c] = dp[r-1][c] + dp[r][c-1] - dp[r-1][c-1] + value[r][c]     # 二维前缀和
        differ = abs(2*dp[r][c] - weight)
        if (differ<answer_value and r*c<answer_area):
            answer = (r,c)
            answer_area = r*c
        else:
            answer = (r, c)
            answer_area = r * c

print(answer[0],answer[1])

第十题

n,k = map(int,input().split())
S = list(map(int,input().split()))
dp =[[0 for i in range(k+1)] for j in range(n+1)] #
for i in range(n):
    dp[i][1]  = 1   #将所有元素都有长度为1的递增序列
for i in range(n):
    for j in range(i): 
        if(S[i]>S[j]):
            for l in range(2,k+1): #也就是在k的
                dp[i][l] = (dp[j][l-1]+dp[i][l]) % 1000007  #动规方程

maxvalue=0
for i in range(n):
    maxvalue = (maxvalue+dp[i][k])%1000007	#相加所有位
print(maxvalue)