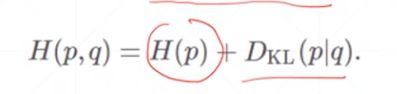Pytorch(3):梯度下降,激活函数与loss,反向传播算法,交叉熵,MNIST测试实战
1、梯度
梯度是一个反向,函数值变大的方向
在做梯度下降时,自变量和因变量是参数和loss函数,参数的值会沿着梯度的方向即loss值更小的方向更新。
2、learning rate
- learning rate如果太小,那么梯度下降太慢,计算时间太长
- learning rate 太大的话,梯度下降可能会反复在局部最小值两端横跳
- 让lr在梯度较大时,大一些,在梯度较小时,小一些。
- 可以在lr上加上每次梯度下降时刻的梯度的平方和再开根号来限制lr的变化:AdaGrad
3、initialization status
梯度下降的初始化会决定最后可以下降到哪个local minimum
4、momentum
可以有助于跳过局部最小值:加入惯性
- 在当前时刻梯度更新的方向不仅仅取决于当前时刻的梯度,还要通过加权考虑前面几个时刻的梯度。这样当曲面平缓,或落在局部最小值上时,该momentum可以加大惯性,使梯度继续沿着最小值的方向更新下去。
w=w-lr*grad
- grad:决定方向
- lr:决定步长
Adam是同时考虑了方向和步长的梯度更新策略
5、激活函数
常用激活函数
- relu: 将小于0的部分不响应,大于0线性相应:让梯度经过激活函数后梯度不变。
- leaky_relu: 小于0的部分也按一定斜率线性相应
- sigmoid 有缺陷,在两端时梯度接近0,梯度无法更新
- tanh: 2sigmoid(2x)-1 :映射到[-1,1]
torch.sigmoid(a) 将输入的值全部映射到[0,1]区间
torch.tanh(a)
torch,relu(a)
6、loss及其梯度
- MSE
- Cross-entropy
第一种:MSE
- L2_norm相比于mse多了一个开根号的步骤
- 使用norm也可以
使用pytorch自动求导
第一种: torch.autograd.grad
x=torch.ones(1)
w=torch.full([1],2)
#w=torch.tensor([1.],required_grad=True)
w.requires_grad_()#告诉系统这个w需要更新
mse=F.mse_loss(torch.ones(1),x*w)
torch.autograd.grad(mse,[w])
第二种:loss.backward
x=torch.ones(1)
w=torch.full([1],2)
#w=torch.tensor([1.],required_grad=True)
mse=F.mse_loss(torch.ones(1),x*w)
mse.backward()
w.grad()#返回w的梯度信息
7、 softmax:
将输出的结果映射到一个维度,使所有输出的总和为1,符合概率分布的特征。适用于分类的时候。
还会使数值较大的经过softmax后相较于原来的与其他值的比例来说变得更大,可以把数值代表的信息放大。
p=F.softmax(a,dim=0)
- 用 p i 对 a j p_i对a_j pi对aj求导时,下标相等时,梯度为正,下标不相等时,梯度为负
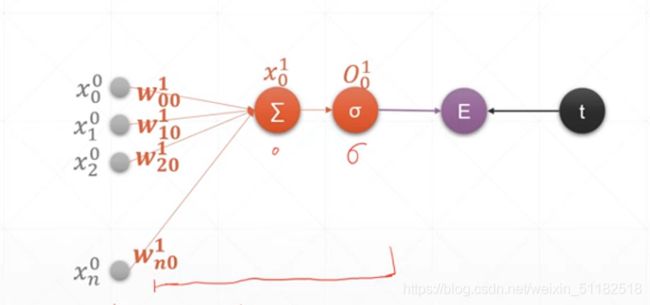
8、感知机的梯度推导
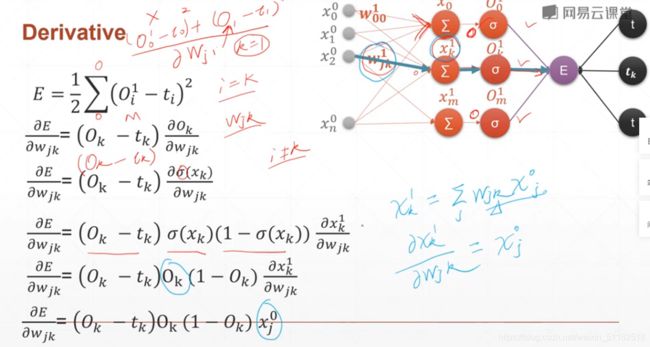
第一类:单输出感知机的后向算法
- O 0 1 O_{0}^1 O01:对于第一层layer,第0值,经过sigmoid函数后的值
- x 0 1 x_{0}^1 x01:对于第一层layer,第0个,通过layer计算后的output
- w n 0 1 w_{n0}^1 wn01对于第一层layer,用于计算第0个output,n代表输入的x的位置。
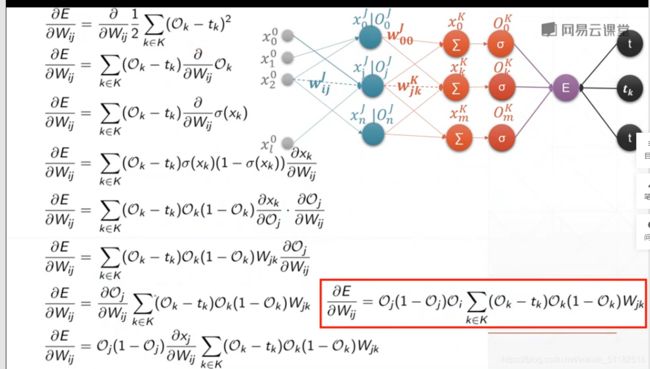
第二类:多输出的感知机的后向算法
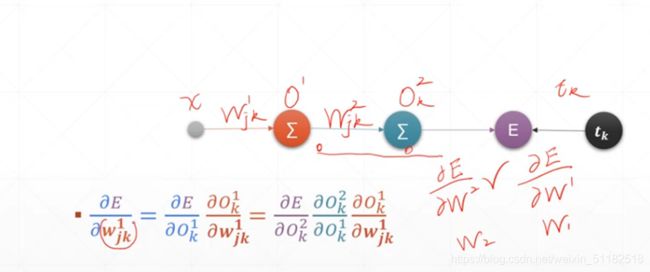
9、链式法则
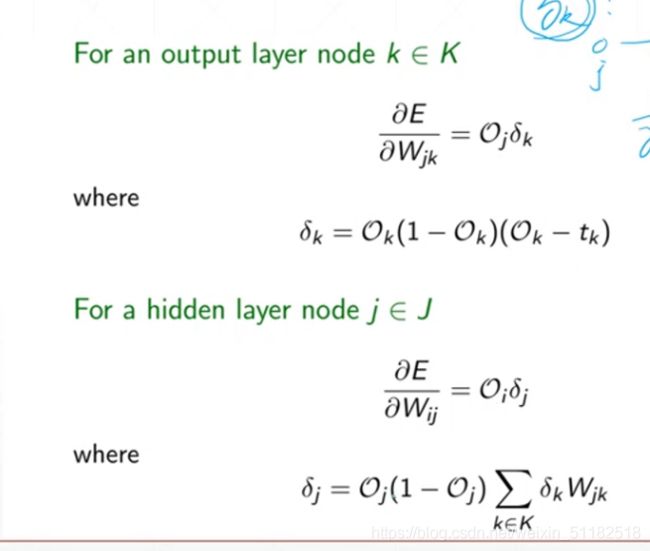
10、反向算法传播
δ k k \delta_{k}^k δkk:表示对于最后经过k层layer输出的sigmoid后的输出值与实际值在后向传播中的值
11、Logistic regression
输入通过linear regression的hidden layer后 经过sigmoid函数将output映射到[0,1]区间。设定一个阈值,把回归问题转为二分类问题。
在logistic regression中,不去最大化准确率
- 有时准确率不变,但是weight改变了,acc无法反映loss随着weight变化的情况
- 梯度不连续,number of correct is not continuous
使用cross-entropy做梯度下降
将输出的output和label当作两个概率分布,计算它们两个的交叉熵
12、交叉熵
- 熵越小,意味着该事件发生的确定性越强,也可以理解为它蕴含的信息很多。
- 当概率为0.5时,熵最大,为完全随机事件
- 概率为0和概率为1时,熵最小为0,一定不可能发生的事情和一定发生的事情都蕴含着大量的信息。
-
p和q相等时,它们完全overlap,即kl散度为0
-
当label值作为one-hot encoding 时,它的熵为0,因为事件的发生是确定的。
为什么使用crossentropy而不是用mse
- sigmoid 函数易发生gradient vanish
- converge slow:聚合得的很慢
- 但是mse求导很便捷,对于简单模型来说,mse可以选择使用。
F.cross_entropy(logits,torch,tensor([3])) #cross-entropy自带了,softmax+log操作
ce=softmax+log+nll_loss
13、多分类问题实战
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
batch_size=200
learning_rate=0.01
epochs=10
'''加载数据集'''
train_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=True, download=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=False, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=batch_size, shuffle=True)
'''初始化w,b'''
w1=torch.randn(200,784,requires_grad=True)#将输出的size放在前面
b1=torch.randn(200,requires_grad=True)#requires_grad:设置为true才可以做梯度下降
w2=torch.randn(200,200,requires_grad=True)
b2=torch.randn(200,requires_grad=True)
w3=torch.randn(10,200,requires_grad=True)
b3=torch.randn(10,requires_grad=True)
torch.nn.init.kaiming_normal_(w1)#将w初始化为一个可以让梯度下降进行得更顺利地值
torch.nn.init.kaiming_normal_(w2)
torch.nn.init.kaiming_normal_(w3)
'''设置nn的计算'''
def forward(x):
[email protected]()+b1
x=F.relu(x)
x = x @ w2.t() + b2
x = F.relu(x)
x = x @ w3.t() + b3
x = F.relu(x)
return x
'''建立优化器和损失函数'''
optimizer=optim.SGD([w1,b1,w2,b2,w3,b3],lr=learning_rate)
criteron=nn.CrossEntropyLoss()
'''开始训练'''
for epoch in range(epochs):
for batch_idx,(data,target) in enumerate(train_loader):
data=data.view(-1,784)
logits=forward(data)
loss=criteron(logits,target)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if batch_idx%100==0:
if batch_idx % 100 == 0:
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
epoch, batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.item()))
test_loss = 0
correct = 0
for data, target in test_loader:
data = data.view(-1, 28 * 28)
logits = forward(data)
test_loss += criteron(logits, target).item()
pred = logits.data.max(1)[1]
correct += pred.eq(target.data).sum()
test_loss /= len(test_loader.dataset)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
代码流程和要点:
- 1、数据集加载
转为tensor格式
设置batch size
shuffle - 2、随机生成w1,b1,w2,b2,w3,b3
要使用nn.init.kaiming_normal_对三个权值的分布做初始化,否则会造成gradient vanishing
导致gradient vanishing的因素:梯度太小,lr太大,初始化有问题 - 3、设置前向算法y=wx+b,还要经过relu激活函数
- 4、设置优化器,设定变量,sgd作为梯度下降策略,给定学习率
- 5、设置loss的函数形式:nn.CrossEntropy
- 6、开始迭代
- 7、对于每个batch,先要reshape输入的data
- 8、将data带入forward算法
- 9、计算loss,logits和target作为目标分布
- 10、optimizer.zero_grad计算梯度
- 11、loss.backward()后向算法
- 12、optimizer.step()更新梯度
- 13、将测试数据reshape后带入forward算法。
- 14、使用logits.data.max(1)[1]找到概率最大的值得索引位置
- 15、pred.eq(target.data).sum(),将每个batch size求得的预测正确的数目相加
14、全连接层
nn.Linear(input_dim,output_dim)#建立一个全连接层
建立一个nn得类的时候必须继承自nn.Module
还需要在代码中使用net=MLP()建立一个网络
使用relu函数:
- nn.ReLU
- F.relu
15、激活函数与GPU加速
- Leaky Relu
相比于sigmoid,做后向算法更新每一层layer的梯度时,relu函数得计算比sigmoid函数求导要简单很多很多
- nn.LeakyReLU
- SELU:更加smooth
- softplus:在(0,0)处加入平滑曲线,使小于0和大于0连续
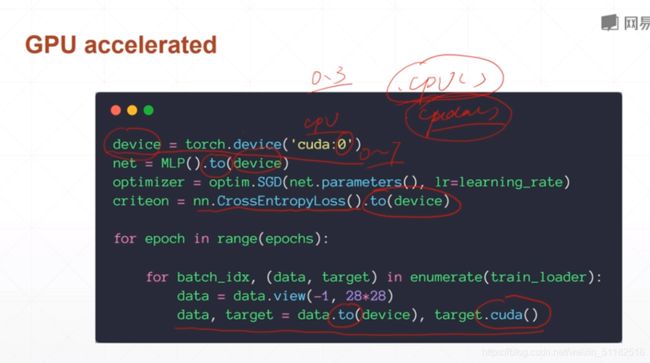
GPU加速:
device=torch.device("cuda:0")
net=MLP().to(device)
criteron=nn.CrossEntropyLoss().to(device)
16、测试
logits=torch.rand(4,10)
pred=F.softmax(logits,dim=1)
pred_label=pred.argmax(dim=1)#[9,5,9,4]
label=torch.tensor([9,3,2,4])
correct=torch.eq(pred_label,label)#[1,0,0,1]
correct.sum().float().item/4#0.5
测试思路
- 将测试集数据取出输入到nn中得到result
- 使用argmax函数将最终结果返回index索引列表
- 使用torch.eq将预测正确的位置为1,错误的为0
- 使用sum()函数统计所有正确的个数再除以batch size得到accuracy