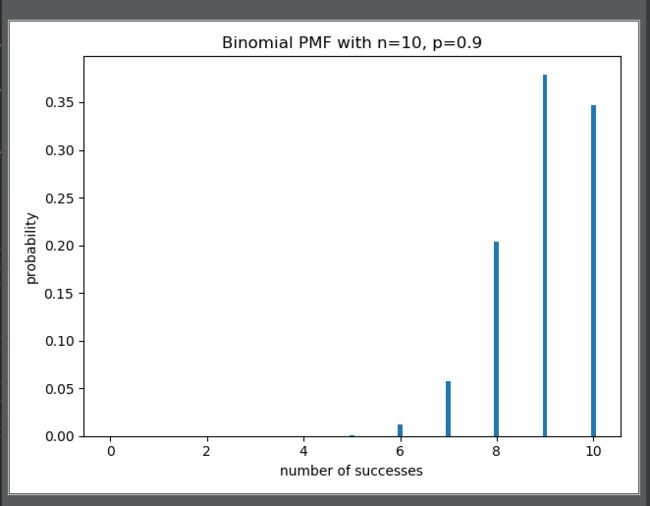
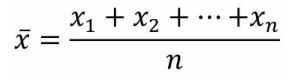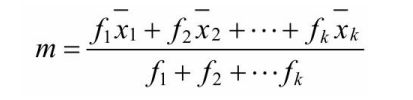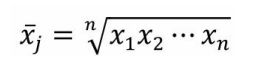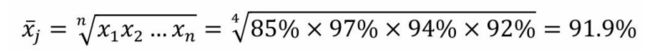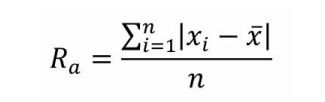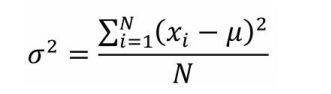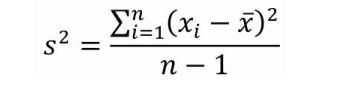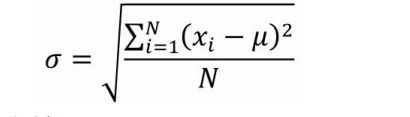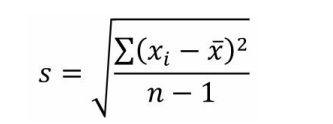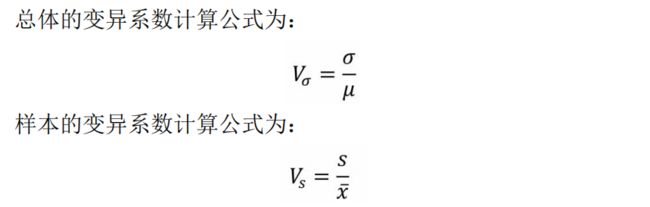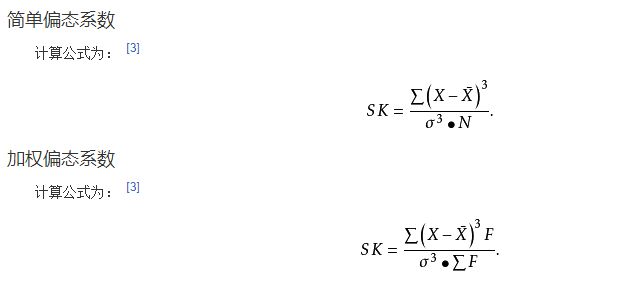早些时间也给自己立下今年的学习目标大数据架构师,为了这一目标也买了不少书籍,下了不少电子书,甚至有报班的想法,后来在修行的道路上有幸遇到居士,且果断的加入到了居士的学习小组,希望借此机会夯实下自己的基础知识。本期知识全部来源于《人人都会数据分析》
主要涉及以下知识点,数据集中趋势,数据离散性,数据分布形态。
(一)数据集中趋势描述:
1、算术平均值:
1.1 简单算术平均值
描述:数据集合的所有数据值相加的和除以数据值个数,简单的说就是总和除以个数。
公式:
应用场景:一个班级平均成绩、一个家庭的人均收入、一个省的人均收入、一个国家的人均收入等。
1.2 加权算术平均值
描述:在简单算术平均基础上上,若每个数据值的权重是不 一样,用加权算术平均值来表示数据集合的集中趋势,即在每个数字上乘以权重值,然后再除以权重总和
公式:
应用场景:公司平均绩效,分不同层级,高层领导,中层领导,底层员工, 每层的绩效系数不一样。
总结:平均值算法有其劣势,受极值(最大,最小值,均值会向这两个部分倾斜)的影响较大,这样不能准确的反映数据的集中情况
2、几何平均值:
描述:指 n 个数字连乘积的 n 次方根,反映了数据之间的乘积关系。
公式:
应用场景:为该食品工厂的生产工艺是连续性生产,只有上一道工序的合格品才能进入下一道工序中,所以每道工序的合格率之间是乘积关系
3、众数:
描述:数据集合中出现次数最多的数值被称为众数,“众里寻他千百度,那人却在灯火阑珊处“,这里的众数就是灯火阑珊下的他。
公式:python中的实现counts = np.bincount([1,2,3,4,5,4,3,2,4]) np.argmax(counts)
应用场景:使用众数制订服装企业的生产计划,看以往数据哪个尺码的衣服销量最好,下批次好多生产等。最后,众数的实际的代表意义只有在数据足够多,且有明显的集中趋势时,才能体
现得最好。否则,不宜用众数代表集中趋势。
4、中位数:
描述:将所有的数值按照它们的大小,从高到低或从低到高进行排序,如果数据集合包含的数值个数是基数,那么排在最中间的数值就是该数据集合的中位数;如果数据集合的数值个数是偶数,那么取最中间两个数值的算术平均值作为中位数
应用场景:使用中位数识破招聘启事的工资陷阱,看工资的中位数和算术平均值的差距,可以反应工资的合理性与可行性
(二)数据离散程度描述
1、极差:
描述:极差又被称为全距,是指数据集合中最大值与最小值的差值,表示整个数据集合能够覆盖的数值距离,两组数据平均值一样时,极差越大的说明数据越离散
公式:
应用场景:使用极差描述气温的变化幅度,可以反应出一天的温暖变化程度,一个月,一个季度一年温度的为年度差异,温度走势情况
2、平均偏差
描述:平均偏差是指一组数中每个数与这组数据的平均值的差取绝对值之和,然后与这组数的个数之比。平均偏差越小表示越稳定
公式:
应用场景:使用平均偏差评价生产线的稳定性,以生产瓶子为例,随机再生产线上拿去100个瓶子,取得每个瓶子的直径,然后用这100个直径做平均偏差计算,看看是否比老生产线的平均偏差小,如果小则说明当前生产线越稳定
3、方差
描述:方差是一组数中各数值与这组数的平均数差的平方和的平均数。相对平均偏差来说方差用平方的方式消除了负数的问题,但是却夸大了数据的离散程度
公式:
样本方方差相对总体方差来说,再数据上偏小,为了提高样本方差的准确率故将分母做了减一处理,分母为n-1的样本方差是总体方差的无偏估计
应用场景:使用标准差(方差)提高巧克力生产线的工艺水平,生产线的稳定性直接表现为产品的重量波动情况,产品总体的方差或标准差越小,说明生产线的生产稳定性越强
4、标准差
描述:总体标准差是方差的正值平方根,样本标准差是样本方差的正值平方根,主要用于衡量数据的离散程度,再均值的基础上衡量数据,标注差越小表示数据越稳定,再行业中有6标准差(SIX SIgma)理论来帮助企业提供生产工艺,降低生产成本;标准差是为了解决方差夸大数据离散程度,一种收敛数据的方式,更能反应数据的离散情况
公式:
样本标准差是在整体标准差的基础分母-1演变二来,用样本数据来衡量总体数量的标准差情况
应用场景:使用标准差(方差)提高巧克力生产线的工艺水平,生产线的稳定性直接表现为产品的重量波动情况,产品总体的方差或标准差越小,说明生产线的生产稳定性越强
5、变异系数(离散系数)
描述:引用书上的解释:方差和标准差虽然能够表示数据集合中每个数值(个案)距离算术 均值的平均偏差距离,但是这个距离的大小程度却不能很好展现,特别是对于算术平均值不同的两个数据集合。如果两者的方差和标准差相等时,那么到底哪个数据集合的离散程度更高、更低或相同?对于这个问题,方差和标准差解决不了,变异系数却可以,
计算方式:变异系数实质上是标准差相对于算术平均值的大小
公式:
应用场景:使用变异系数客观评定员工绩效,陈某每小时平均生产40个零件,标准差是5件。王某每小时平均生产80个零件,标准差为6件。试问哪个工人的产量稳定性比较好呢? 这里不能简单的说标准差越小的表现越好, 这里要借助变异系数来反应正式情况
6、四分位极差
描述:四分位差 IQR(四分位距):是上四分位数和下四分位数之差。它反映了中间50%的数据的离散程度,其数值越小,说明中间的数据越集中,反之则越分散。同样不受极值的影响。将所有数据按照大小,从低到高进 行排序排在四分之一位置的数值即为第一四分位数Q1;排在四分之二位置的数值为第二四分位数Q2 ,也就是中位数;排在四分之三位置的数值为第三四分位数Q3。这三个四分位数将整个数据集合分成四等分
7、顺序数据
描述:可以进行排序,表明事物之间的大小、优劣关系等,是只能归于某一有序类别的非数字型数据。顺序数据虽然也是类别, 但这些类别是有序的。比如将产品分为一等品、二等品、三等品、次品等;考试成绩可以分为 优、良、中、及格、不及格等;一个人的受教育程度可以分为小学、初中、高中、大学及以上; 一个人对某一事物的态度可以分为非常同意、同意、保持中立、不同意、非常不同意,等等
8、异众比率
描述:异众比率指的是总体中非众数次数与总体全部次数之比。换句话说,异众比率指非众数组的频数占总频数的比例。
公式:
应用场景:异众比率主要适合测度分类数据的离散程度,当然,对于顺序的数据以及数值型数据也可以计算异众比率。它虽然也是一个反映离散程度的相对指标,但是与标准差系数不同。 异众比率主要用于衡量众数对一组数据的代表程度。异众比率越大,说明非众数组的频数占总频数的比重越大,众数的代表性就越差;异众比率越小,说明非众数组的频数占总频数的比重越小,众数的代表性越好。
(三)数据分布形态描述
1、偏态系数
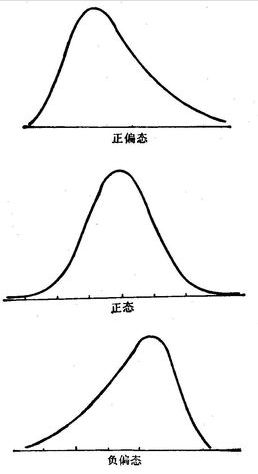
描述:偏态系数又称偏差系数,说明随机系列分配不对称程度的统计参数,偏态系数以平均值与中位数之差对标准差之比率来衡量偏斜的程度,用SK表示偏斜系数:偏态系数小于0,因为平均数在众数之左,是一种左偏的分布,又称为负偏。偏态系数大于0,因为均值在众数之右,是一种右偏的分布,又称为正偏,偏态系数绝对值越大,偏斜越严重。
偏态系数用来度量分布是否对称。正态分布左右是对称的,偏度系数为0。较大的正值表明该分布具有右侧较长尾部。较大的负值表明有左侧较长尾部。偏度系数与其标准误的比值同样可以用来检验正态性。
公式:
偏态系数值说明:
2、峰态系数
描述:峰度系数是用来反映频数分布曲线顶端尖峭或扁平程度的指标。有时两组数据的算术平均数、标准差和偏态系数都相同,但他们分布曲线顶端的高耸程度却不同。用来度量数据在中心聚集程度。在正态分布情况下,峰度系数值是3。>3的峰度系数说明观察量更集中,有比正态分布更短的尾部;<3的峰度系数说明观测量不那么集中,有比正态分布更长的尾部,类似于矩形的均匀分布。峰度系数的标准误用来判断分布的正态性。峰度系数与其标准误的比值用来检验正态性。如果该比值绝对值大于2,将拒绝正态性
公式:
实践部分:实践部分就不一一贴图了,篇幅太大(部分),动手部分还需要加强