随机变量专题及其python实现(概率分布，二项分布，正态分布，卡方分布，t分布，F分布及变量相关性分析等)

统计分析是可以帮助人们认清、刻画不确定性的方法。总体是某一特定事物可能发生结果的集合， 随机变量(Random Variable) 则是一个不确定事件结果是数值函数(Function)。也就是说，把不确定事件的结果用数值来表述，即得到随机变量。随机变量又分为 离散型随机变量(Discrete Random Variable) 和 连续型随机变量(Continuous Radom Variable)。

1. 概率与概率分布

概率(Probability)是用于刻画事物不确定性的一种测度(Measure)，根据概率的大小，我们可以判断不确定性的高低。

1.1离散型随机变量

1.1.1概率质量函数(PMF)

假设X是一个离散型随机变量，其所有可能取值为集合{a_k}，k=1,2,…,我们定义X的概率质量函数(Probability Mass Function) 为：
$f_X(a_k)=P\{X=a_k\},k=1,2,\cdots$
概率质量函数可以量化地表达随机变量X取每个数值可能性的大小

1.1.2 累计分布密度函数(CDF)

对于离散型随机变量，累计分布函数可以用概率质量函数累加来获得：
$F_X(a)=P\{X\le a\}=\sum _{i:a_i\le a}{f}_X(a_i)$

1.1.3 Python的实现

在Python中我们可以通过Numpy包的random模块中的choice()函数来生成服从待定的概率质量函数的随机数。
choice()函数：

• choice(a, size=None, replace=True, p=None)
  参数a: 随机变量可能的取值序列。
  参数size: 我们要生成随机数数组的大小。
  参数replace: 决定了生成随机数时是否是有放回的。
  参数p：为一个与x等长的向量，指定了每种结果出现的可能性。

计算频数分布使用value_counts()函数

# 以数组形式
import numpy as np
import pandas as pd

RandomNumber=np.random.choice([1,2,3,4,5],\
size=100, replace=True,\
p=[0.1,0.1,0.3,0.3,0.2])
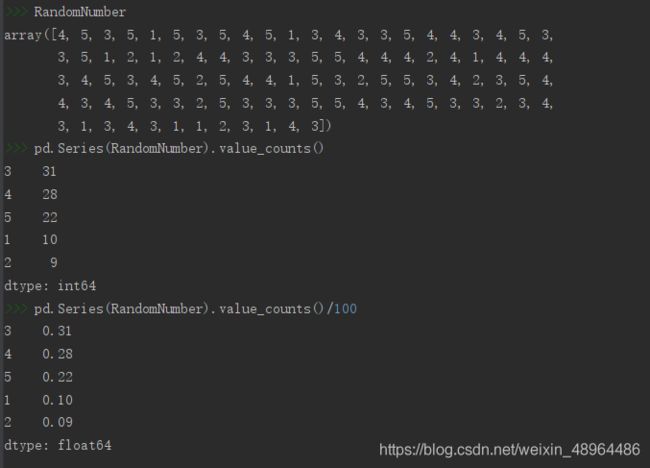
pd.Series(RandomNumber).value_counts() # 计算频数分布value_counts()函数
pd.Series(RandomNumber).value_counts()/100  #计算概率分布

结果呈现：

• 增大size参数，即生成随机数的数目，得到的结果则会更接近设定的概率。

1.2 连续型随机变量

若随机变量X是连续的，我们则不再能通过概率质量函数来刻画随机变量只随机性，对任意a_k都有$P\{X=a_k\}=0$。
连续型随机变量没有PMF。对于连续型随机变量，累积分布函数

$F_X(a)=P\{X\le a\}$可以表达为：

$F_X(a)={\int }_{-\infty }^a{f}_X(x)dx$

其中$f_X=\frac{d{F}_X(x)}{dx}$，被称作概率密度函数
(Probability Density Function)(PDF)，X的取值落在某个区间的概

率可以用概率密度函数在这个区间上的积分来求得。

算法逻辑：

• 使用stats模块kde包中的gaussian_kde()可以估计数据的概率密度，在其中传入我们要统计的Series类型的变量名即可，得到的是一个“scipy.stats.kde.gaussian_kde”类型的对象，我们暂先给其命名为density。
• 然后设定好分割区间，设为数组格式，暂将该对象命名为bins。
• 注意，这次与以往绘图不同，这次是以研究的对象数据为行进行绘图。
• 使用上边得到的数据类型density，以 density(bins)格式的语法可以得到一个以设定的分割区间为界限的概率密度数组，让将density(bins)这个对象作为行传入plot即可。
• 如果要绘制累计分布函数图，则只需在上边的density(bins)对象后再调用一下cumsum()函数，对数组数据进行累加后在传入即可。

以2020年沪深300指数(399300.SZ)的收益率(日涨跌幅)数据为例：

# 调取数据
import numpy as np
import tushare as ts
import pandas as pd
token = 'Your Token'   # 输入你的接口密匙，获取方式及相关权限见Tushare官网。
pro = ts.pro_api(token)
df = pro.index_daily(ts_code='399300.SZ')  
df['trade_date'] = pd.to_datetime(df['trade_date'])  
df.set_index(['trade_date'], inplace=True)  # 将日期列作为行索引
df = df.sort_index() 

# 实现概率分布
import matplotlib.pyplot as plt
from scipy import stats
density = stats.kde.gaussian_kde(df.pct_chg['2020']) #研究数据格式化
bins=np.arange(-5,5,0.02)  # 设定分割区间

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.subplot(211)
plt.plot(bins,density(bins))
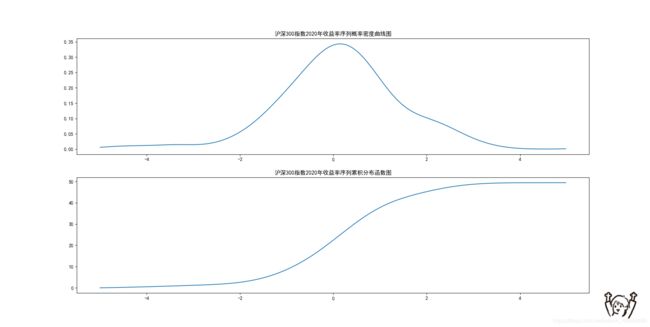
plt.title('沪深300指数2020年收益率序列概率密度曲线图')
plt.subplot(212)
plt.plot(bins,density(bins).cumsum())
plt.title('沪深300指数2020年收益率序列累积分布函数图')
plt.show()

结果展示如下：

---

2. 期望值与方差

可以用样本数据的平均值来刻画样本的中心位置，期望(Expectation)是随机变量所有可能取的结果的均值，用来呈现总体的中心位置。对于离散型随机变量，期望是该随机变量所有可能结果的取值与其概率的乘积之和：
$E(X)=\sum _k{a}_k{f}_X(a_k)=\sum _k{a}_{k}P\{X=a_k\}$
方差(Variance)则是:
$Var(X)=E{\left[X-E\right]}^2=\sum _k\left[a_k-E(X{)}^2\right]P\{X=a_k\}$
对于一类特殊的离散型随机变量：伯努利(Bernoulli Random Variable)随机变量，伯努利随机变量X只能取到两个值，0或者1，对应的概率质量函数为：
$f_X(a)=P(X=a)=\{\begin{array}{ll}p,& a=1\\ 1-p,& a=0\end{array}$

伯努利随机变量的期望值$E(X)=p$

方差为$Var(X)=(1-p)\cdot p$

若随机变量X为连续型随机变量，其概率密度函数为$f_X$，则期望为：$E(X)={\int }_{-\infty }^{\infty }a{f}_X(a)da$

方差为：$Var(X)={\int }_{-\infty }^{\infty }{\left[a-E(X)\right]}^2{f}_X(a)da$
随机变量可能的取值有很多(比如连续型随机变量的取值为无穷)，但其观测值(实际值)个数有限，因此现实中随机变量的概率分布、期望、方差等特征值通常是不可知的，推断统计就是透过其观测值的集合——样本数据来刻画这些特征的。

---

3. 二项分布

3.1二项分布概述及其与伯努利分布的差别

研究伯努利分布时，我们关注的期望是进行一次试验结果的期望值，这样的结果有两种情况，所以伯努利分布也称“两点分布”。
而研究二项分布时，我们关注的是n次试验的结果，这样的结果有多种组合。
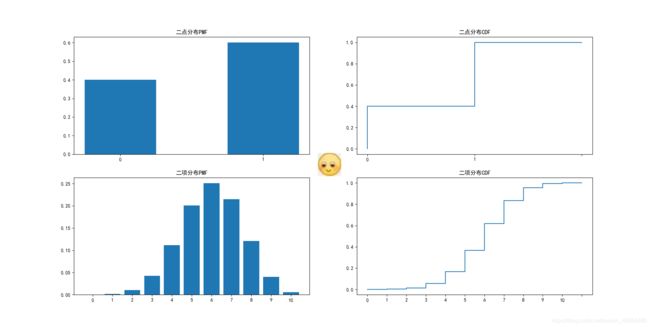
为直观说明，假设二点分布结果0的概率为0.4，结果为1的概率为0.6；
二项分布结果为0的概率为0.4，结果为1的概率为0.6，且进行十次。
则：

n = 10
p1 = 0.6
p2 = 0.6
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.subplot(221)
plt.bar(['0','1'], [1-p1,p1], width=0.5)
plt.title("二点分布PMF")
plt.subplot(222)
plt.plot(['0','0','1','1',' '], [0, 0.4, 0.4, 1.0,1.0])
plt.title("二点分布CDF")
plt.subplot(223)
b = [stats.binom.pmf(i,10,0.6) for i in range(0,11)]
plt.bar([str(i) for i in range(0,n+1)],b)
plt.title('二项分布PMF')
plt.subplot(224)
plt.title("二项分布CDF")
c = [str(i//2) for i in range(0,2*(n+1))]
c.append('')
d = [stats.binom.cdf(i//2,10,0.6) for i in range(0,22)]
d.insert(0,0)
plt.plot(c,d)
plt.show()

展示结果：

当np≥10，n(1-p)≥10都满足时，二项分布可以近似为正态分布。

3.2 Numpy生成二项分布随机数

在Numpy库中可以使用binomial()函数来生成二项分布随机数。
形式为：binomial(n, p, size=None)
参数n是进行伯努利试验的次数，参数p是伯努利变量取值为1的概率，size是生成随机数的数量。

np.random.binomial(100, 0.5, 20)

3.3 二项分布的PMF与CDF

3.3.1 PMF及其图像绘制

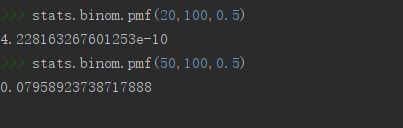
# 求100次试验，20次成功的概率，p=0.5
stats.binom.pmf(20,100,0.5)
# 求100次试验，50次成功的概率,p=0.5
stats.binom.pmf(50,100,0.5)

图像绘制

#传入时n+1是因为10次实验有十一种可能的结果组合。
n=10   # 十次试验
p=0.5  
plt.rcParams['font.sans-serif'] = ['SimHei']
b = [stats.binom.pmf(i, n, p) for i in range(0,n+1)]
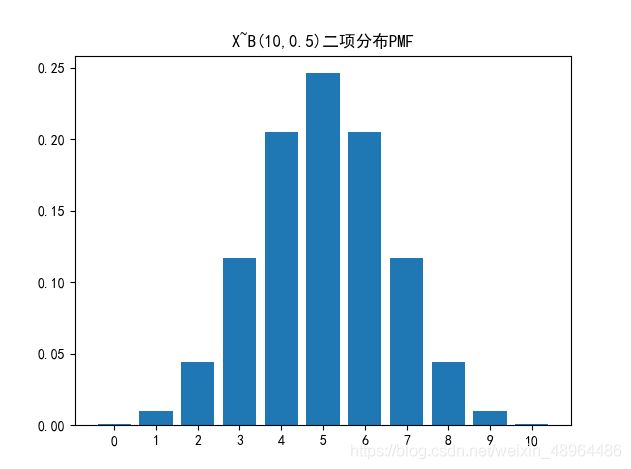
plt.bar([str(i) for i in range(0,len(b))],b)
plt.title('X~B({},{})二项分布PMF'.format(n,p))
plt.show()

3.3.2 CDF及其图像绘制

可以直接用pmf()函数解决这个问题。

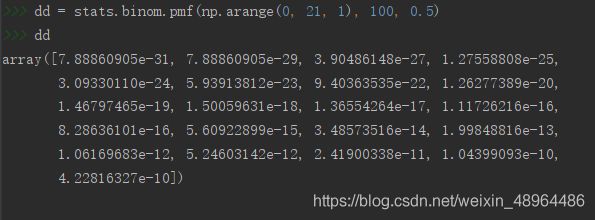
#stats.binom.pmf函数很神奇，传入的第一个参数是数字(指定伯努利试验成功的次数)，生成结果就也是一个数字。如果传入的第一个参数是数组，则会将会以该数组的shape输出其中每个数字成功次数的条件下，对应的概率。
dd = stats.binom.pmf(np.arange(0, 21, 1), 100, 0.5)
dd

# 然后对数组求和即求出小于等于20次发生这一事件的概率
dd.sum()

此外，也可以用binom中的cdf()函数来直接解决这个问题

# 依然100次试验成功20次，每次p=0.5
stats.binom.cdf(20,100,0.5)

图像绘制

n=10   # 十次试验
p=0.5
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.title('X~B({},{})二项分布CDF'.format(n,p))
c = [str(i//2) for i in range(0, 2*(n+1))]
c.append('')
d = [stats.binom.cdf(i//2, n, p) for i in range(0, 22)]
d.insert(0,0)
plt.plot(c,d)
plt.show()

3.3.3 二项分布在金融市场的应用

二项分布常常用于描述金融市场中只有两个结果的重复事件。
如研究平安银行股票2020年数据：

# 导入相关模块
import numpy as np
import tushare as ts
import pandas as pd
from scipy import stats
# 设定好接口  注意这句不能照抄，需要输入自己的接口密匙
token = 'Your token'   # 输入你的接口密匙，获取方式及相关权限见Tushare官网。
pro = ts.pro_api(token)
# 获取数据
df = pro.daily(ts_code='000001.SZ')  # daily为tushare的股票日线数据接口。
df['trade_date'] = pd.to_datetime(df['trade_date'])  
df.set_index(['trade_date'], inplace=True)  # 将日期列作为行索引
df = df.sort_index() 
ret = df.pct_chg['2020']

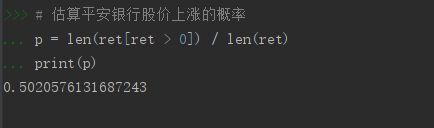
# 估算平安银行股价上涨的概率
p = len(ret[ret > 0]) / len(ret)
print(p)

# 估计十个交易日中，平安银行有六个交易日上涨的概率
prob = stats.binom.pmf(6,10,p)
print(prob)

---

4. 正态分布

4.1 正态分布概述

正态分布(Normal Distribution)又名高斯分布(Gaussiam Distribution)，是人们最常用的描述连续型随机变量的概率分布。在金融学研究中，收益率等变量的分布假定为正态分布或者对数正态分布(取对数后服从正态分布)。因为形状的原因，正态分布曲线也被经常称为钟形曲线。
正态分布分布律： 若随机变量X满足服从一个数学期望为u, 方差为${\sigma }^2$的正态分布，记为X ~$(N,{\sigma }^2)$，则X的取值范围为($-\infty ,+\infty$)，其概率密度为：

$f_X(x)=\frac{1}{\sqrt{2\pi \sigma }}exp\left[\frac{-(x-u{)}^2}{2{\sigma }^2}\right]$
均值越大图像越靠右，方差越小图像越瘦高
服从正态分布的变量X满足其线性变换aX+b~($au+b,a^2{\sigma }^2$)。
若令a = $\frac{1}{\sigma }$，b = $\frac{-u}{\sigma }$，即可得到标准正态分布，该过程即标准化，数学式记作：

$Z=\frac{X-u}{\sigma }$ ~ N$(0,1)$
任何正态分布都可以进行标准化，转变成标准正态分布。

4.2 Python正态分布相关函数

正态分布随机数的生成函数是normal()，其语法为：
normal(loc=0.0, scale=1.0, size=None)

• 参数loc：表示正态分布的均值
• 参数scale：表示正态分布的标准差，默认为1
• 参数size：表示生成随机数的数量

# 生成五个标准正态分布随机数
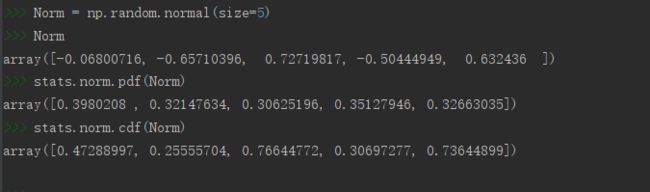
Norm = np.random.normal(size=5)
# 求生成的正态分布随机数的密度值
stats.norm.pdf(Norm)
# 求生成的正态分布随机数的累积密度值
stats.norm.cdf(Norm)

绘制正态分布PDF

# 注意这里使用的pdf和cdf函数是norm包里的
u=0  
sigma=1
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.title('X~N({},{})正态分布PDF'.format(u,sigma**2))
x = np.linspace(-5,5,100000)  # 设定分割区间
y1 = stats.norm.pdf(x,u,sigma**2)
plt.plot(x,y1)
plt.tight_layout()  # 自动调整子图，使之充满画布整个区域
plt.show()

图像效果：

绘制正态分布CDF

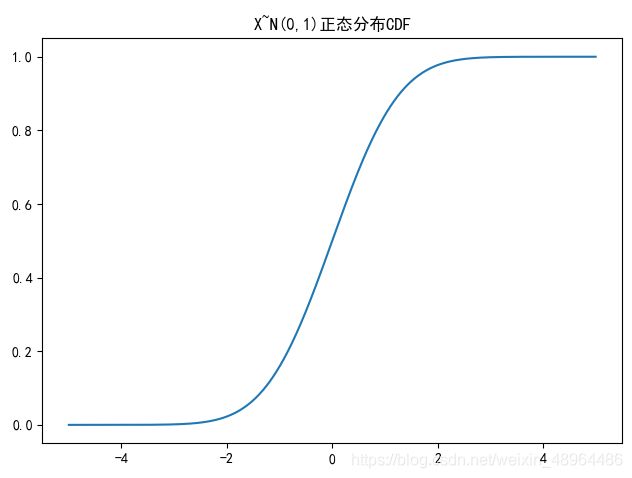
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.title('X~N({},{})正态分布CDF'.format(u,sigma**2))
x = np.linspace(-5,5,100000)  # 设定分割区间
y2 = stats.norm.cdf(x,u,sigma**2)
plt.plot(x,y2)
plt.tight_layout()  
plt.show()

图像效果：

4.3 正态分布在金融市场的应用

VAR(Value at Risk)，即在险价值。是指在一定概率水平(α%)下，某一金融资产或金融资产组合在未来特定一段时间内的最大可能的损失，该定义可表达为：$P\{X_t<-VaR\}$ = α%
其中，随机变量X_t为金融资产或金融资产组合在持有期$\Delta t$内的损失，1-α%被叫做VaR的置信水平。
这里用到了ppf() 函数，来获取指定分位数的累积密度值。
假设平安银行股价2020年日收益率序列服从正态分布，下面用Python来求解当概率水平为5%时平安银行股价日收益率在2021年初个交易日的VaR:

# 上边已经定义过ret变量了，为平安银行2020年股价日收益率数据，
# 这里直接接着使用
ret_mean = ret.mean()   # 求均值
ret_variance = ret.var()  # 求方差
# 查询累积密度值为0.05的分位数
stats.norm.ppf(0.05, ret_mean, ret_variance**0.5)

也就是说，在2021年的第一个交易日，有95%概率平安银行股票的损失不会超过3.475523569%。
（虽然当天实际跌了3.83，产生了异常值。）

---

5. 其他连续分布

5.1 卡方分布

若Z₁, Z₂, … Z_n,为n个服从标准正态分布的随机变量，则变量：

$X=Z_1^2+Z_2^2+\cdots +Z_n^2$
服从自由度(Degree of Freedom)为n的卡方分布，

通常表示为$X^2$~${\chi }^2$

因为n的取值可以不同，所以卡方分布是一族分布而不是一个单独的分布。根据X的表达式，服从卡方分布的随机变量值不可能取负值，其期望值为n，方差为2n。

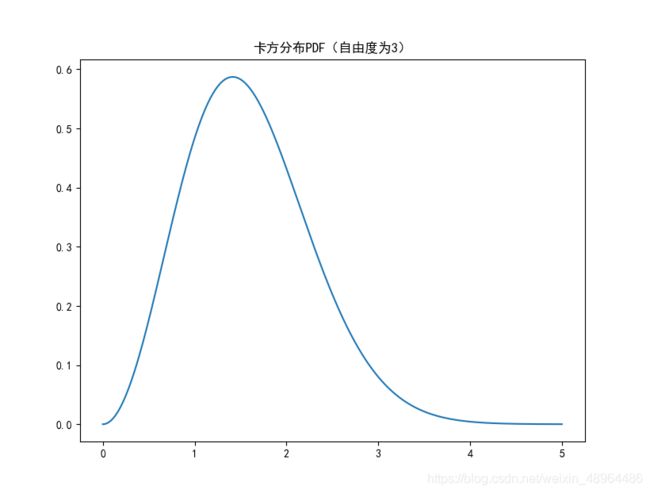
plt.plot(np.arange(0, 5, 0.002),\
stats.chi.pdf(np.arange(0, 5, 0.002), 3))
plt.title('卡方分布PDF（自由度为3）')

生成图像如下：

卡方分布以0为起点，分布是偏斜的，即非对称的，在自由度为3的卡方分布下，大多数值都小于8，查表可知只有5%的值大于7.82%。

---

5.2 t分布

若随机变量$Z$ ~ $N(0,1)$，$Y$ ~ ${\chi }^2(n)$，且二者相互独立，
则变量$X=\frac{Z}{\sqrt{Y/n}}$服从自由度为n的t分布，

可以记作$X$~$t(n)$。
类似卡方分布，t分布也是整整一族，自由度n不同t分布即不同。
t分布变量取值范围为（$-\infty ,+\infty$），其期望值与方差存在于否，取值大小均与t分布的自由度有关。

• t(1)分布无有限期望值。
• t(2)有有限期望值，但方差不存在。
• n>2时，t(n)才同时有有限的期望值和方差，其中期望值为0，方差为n/(n-2)，因此自由度越大，变量的方差越小，也就是说分布的离散程度越小。

下边使用Python绘制不同自由度下的t分布的概率分布图：

x = np.arange(-4,4.004,0.004)
plt.plot(x, stats.norm.pdf(x), label='Normal')
plt.plot(x, stats.t.pdf(x,5), label='df=5')
plt.plot(x, stats.t.pdf(x,30), label='df=30')
plt.legend()

结果如图所示：

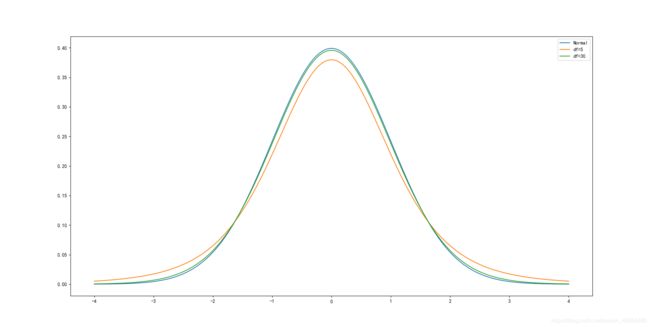
t分布的pdf曲线是以0为中心，左右对称的单峰分布，其形态变化与自由度n的大小有关，自由度越小，分布越分散；自由度越大，变量在其均值周围的聚集程度越高，也越接近标准正态分布曲线。
自由度为30时，t分布已经接近标准正态分布曲线。相较于标准正态分布，t分布的密度函数呈现出“尖峰厚尾”的特点。在现实中资产收益率分布往往呈现这种形态，因此t分布在对实际抽样结果的刻画上更为精确。t分布是在推断统计中常用的分布。
————

5.3 F分布

若Z，Y为两个独立的随机变量，且$Z$~${\chi }^2(m)$、$Y$~${\chi }^2(n)$，

则变量$X=\frac{Z/m}{Y/n}$服从第一自由度为m，第二自由度为n的F分布。

记作X~$F(m,n)$

变量X是两个卡方变量(非负)之比，因此X的取值范围也为非负，其期望和方差存在于否取决于第二自由度n。

n > 2时，才存在期望，为$\frac{n}{n-2}$

n > 4时，才存在方差，为$\frac{2n^2(m+n-2)}{m(n-2{)}^2(n-4)}$

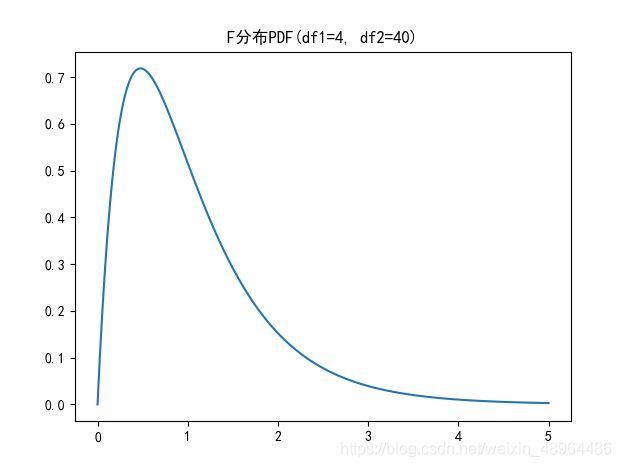
plt.plot(np.arange(0,5,0.002),\
stats.f.pdf(np.arange(0,5,0.002), 4, 40))
plt.title('F分布PDF(df1=4, df2=40)')

它的概率密度函数形态如图所示

---

6. 变量的关系

我们面对的多个随机变量，之间可能会有互相影响。

6.1 联合概率分布

多个变量之间的联合行为可以用联合概率分布(Joint Probability Distribution)来刻画。
若变量X, Y是离散的，其所有可能取值的集合为{a_k}和{b_k}, k=1，2，…，
则X，Y的联合概率质量函数(Joint Probability Mass Function)为:
$f_{X,Y}(a,b)=P\{X=a_i且Y=b_j\}$, i,j=1,2…

双变量X和Y的联合累积分布函数(Joint Cumulative Distribution Function)为： $F_X,Y(a,b)=P\{X\le a且Y\le b\}$

• 当X和Y是离散型的：
  $F_{(X,Y)}(a,b)=\sum _{i:a_i\le a}\sum _{j:b_j\le b}P\{X=a_i且Y=b_j\}=\sum _{i:a_i\le a}\sum _{j:b_j\le b}{f}_{X,Y}(a_i,b_j)$
• 当X和Y是连续型的：
  $F_{(X,Y)}(a,b)={\int }_{-\infty }^a{\int }_{-\infty }^b{f}_{X,Y}(x,y)dxdy$

其中$f_{X,Y}(x,y)dxdy$是联合概率密度函数(Joint Probability Density Function)>
若已知X和Y的联合概率分布，则X的期望值为：
$E(X)=\sum _i\sum _j{a}_i{f}_{X,Y}(a_i,b_j)$

$=\sum _i{a}_i\sum _j{f}_{X,Y}(a_i,b_j)$

$=\sum _i{a}_i{f}_X(a_i)$

其中$f_X(a_i)=\sum _j{f}_{X,Y}(a_i,b_i)$为变量X的边际概率函数(Marginal Probability Function)，代表的是变量X自己的概率分布，所以这里$f_X(a_i)$依然满足$f_X(a_k)=P\{X=a_k\}$定义式。同理可得$E(Y)=\sum _j{b}_j{f}_Y(b_j)$，其形式与单变量的形式无差别。方差求解亦是如此。

---

6.2变量的独立性

如果随机变量X和Y的联合累积分布函数满足：

$F_{(X,Y)}(a,b)=F_X(a)F_Y(b)$

则称X和Y是独立的，否则二者是相依的。

两变量的独立关系也可以表达成，

$f_{X,Y}(a,b)=f_X(a)f_Y(b)$

对于离散型随机变量，此式等价于

$P\{X=a且Y=b\}=P\{X=a\}P\{Y=b\}$
变量之间的相互独立是众多统计分析的基本假设，也是变量之间的基本关系。

---

6.3 变量的相关性

随机变量X和Y的协方差(Covariance)可以衡量二者之间的关系，描述的是两随机变量与各自期望的偏差共同的变动状况，表达式为：
$Cov(X,Y)=E\left[(X-E(X))(Y-E(Y))\right]$
协方差为正说明，平均而言变量X、Y与各自期望的偏差呈同方向变动；如果为负，则为反方向变动。
协方差有如下性质：

• $Cov(X,Y)=Cov(Y,X)$
• $Cov(aX,bY)=abCov(Y,X)$ (a,b是常数)
• $Cov(X_1+X_2,Y)=Cov(X_1,Y)+Cov(Y,X_2)$

第二个性质说明，协方差受比例影响，并不能准确地衡量两变量相关性的大小。，不能直接衡量两变量相关性强弱。对协方差进一步处理，清除比例的影响，于是就有了相关系数(Correlation Coefficient):

${\rho }_{X,Y}=\frac{Cov(X,Y)}{{\sigma }_X{\sigma }_Y}$

相关系数取值范围为[-1,+1]
ρ=0时，说明两个变量是不相关的。
0<ρ<1时， 说明两变量呈正向的线性关系
-1<ρ<0时，说明两变量呈负向的线性关系。

aX和bX的相关性：

${\rho }_{aX,bY}=\frac{Cov(aX,bY)}{\sqrt{Var(aX)}\sqrt{(Var(bY))}}$

$=\frac{abCov(X,Y)}{|a|{\sigma }_X|b|{\sigma }_Y}$

$=\pm {\rho }_{X,Y}$

如果变量Y是X的线性变换，满足Y=a+bX，则二者之间的相关系数为：‘
${\rho }_{X,Y}=\frac{Cov(X,a+bX)}{{\sigma }_X\sqrt{Var(a+bX)}}$

$\frac{bVar(X)}{|b|Var(X)}=\pm 1$

---

6.4 上证指数与深证成指相关性分析

上证指数和深证成指是股票市场常用的反映股票市场情况的指数，我们认为两个指数的日收益率可以存在相关的关系。代码如下：

import numpy as np
import tushare as ts
import pandas as pd
token = 'Your Token'   # 输入你的接口密匙，获取方式及相关权限见Tushare官网。
pro = ts.pro_api(token)
# 深证成指
SZindex = pro.index_daily(ts_code='399001.SZ')
SZindex['trade_date'] = pd.to_datetime(SZindex['trade_date'])
SZindex.set_index(['trade_date'], inplace=True)
SZindex = SZindex.sort_index()
# 上证指数
SHindex = pro.index_daily(ts_code='000001.SH')
SHindex['trade_date'] = pd.to_datetime(SHindex['trade_date'])
SHindex.set_index(['trade_date'], inplace=True)
SHindex = SHindex.sort_index()

# 用2020年日收益率数据绘制散点图
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
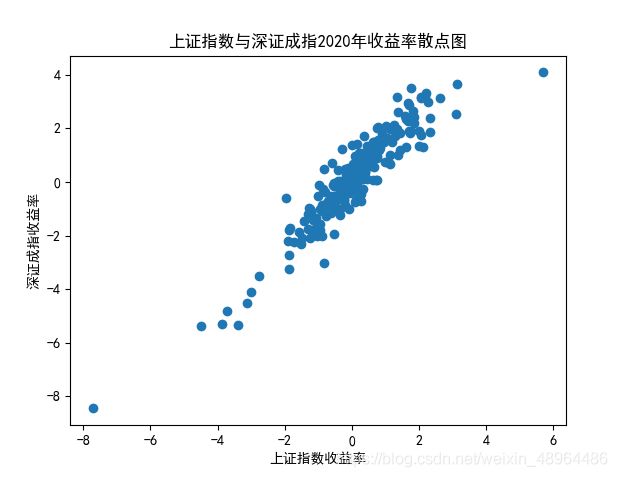
plt.scatter(SHindex.pct_chg['2020'],SZindex.pct_chg['2020'])
plt.title('上证指数与深证成指2020年收益率散点图')
plt.xlabel('上证指数收益率')
plt.ylabel('深证成指收益率')
plt.show()

生成图像展示如下：

# 计算上证综指和深证成指收益率相关系数
SHindex.pct_chg['2020'].corr(SZindex.pct_chg['2020']) 

相关系数为0.9308847411746248，可以认为二者存在较强的相关性，二者呈现正向的线性关系。

---