数字光栅投影技术——相移轮廓术（PSP）

1. 前言

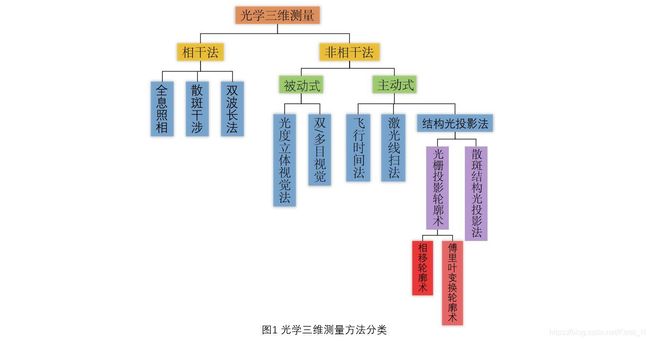
  光学三维测量技术种类繁多，其中结构光投影法是一种非常流行的非接触式测量方法，被广泛地应用于逆向工程、工业检测、口腔医学、文物修复、机器人导航等领域。
  数字光栅投影轮廓术（Fringe Projection Profilometry, FPP）作为最具代表性的结构光投影技术，具有成本低、测量速度快、视场大、分辨率高等特点。FPP中两种主要的相位测量技术是（时域）相移轮廓术（Phase Shifting Profilometry, PSP）和（空域）傅里叶变换轮廓术（Fourier Transform Profilometry, FTP）。FTP是一种基于空间滤波的单帧光栅投影法。本次介绍的对象是PSP技术。不同于FTP，PSP需要至少投射三幅相移光栅图案，但是具有更高的空间分辨率和相位测量精度，并对环境光和物体表面反射率的变化更加鲁棒。由于其多帧测量特性，当测量动态场景时，尤其当帧间间隔内的物体运动不可忽略时将导致相位误差。但近年来，相机、投影等硬件水平有了较大的提上，PSP技术已逐渐应用于动态场景的高速实时三维测量。

2. 光栅投影的三维测量原理

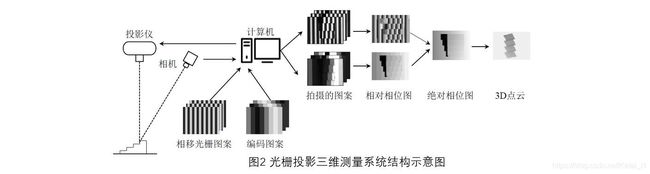
  光栅投影三维测量系统主要由相机(Camera)和投影仪(Projector)组成，测量原理如图2所示。投影仪向待测物投射一组编码图案,编码图案受到待测物表面高度变化引起的调制，并由相机捕获调制后的编码图案；然后，通过解码获得待测物表面上各点在投影仪图像坐标系下的像素坐标；最后，根据三角测量原理计算出待测物表面各点在世界坐标系下的三维坐标。

2.1 相位的获取

  过去的几十年中，涌现出多种相移算法，诸如三步相移算法、四步相移算法、双三步相移算法、改进的2+1 步相移算法等。这些相移算法所使用的光栅图像的数量不同，除此之外，它们还具有一些相似的特征：(1)可获取像素级测量精度，(2) 减轻受环境光的影响，(3) 获取的相位值位于[0,2$\pi$)区间(有的文献中位于[-$\pi$,$\pi$]区间，实质上是一样的)，(4) 使用的光栅图像数越多，获取的精度越高。在这些相移算法中，三步相移法因为使用的光栅图像的数量最少而被广泛地应用于高速测量领域。
  三步相移法中使用的三幅光栅图可表示为：

式中：i 为第 i 次相移；I_i为第 i 幅相移图上(m,n)点处的灰度值； I’(m,n)为背景灰度值；I’’(m,n)为调制的幅值；$\theta$(m,n) 为待求相位；$\alpha$_i为第 i 幅相移图的相移值。
令相移分别为 $\alpha$₁=-$\pi$/3，$\alpha$₂=0 ，$\alpha$₃=$\pi$/3 ，由等式(2.1)求得相位为：

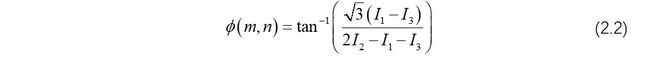
式(2.2)获取的相位为相对相位（Relative Phase，也称包裹相位 Wrapped Phase），需对其进行解包裹获取绝对相位(Absolute Phase)才能求取相位-高度映射关系。解包裹方法分为时域解相法（Temporal Phase Unwrapping）和空域解相法（Spatial Phase Unwrapping），以后再作介绍。

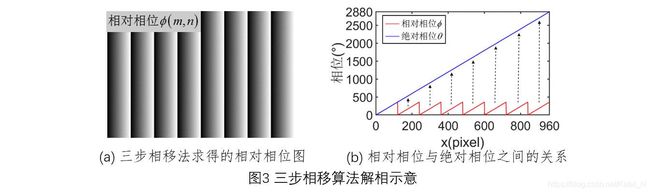
2.2 相位——高度映射

  获得每个像素点的绝对相位之后，便可求取物体的深度信息 Z，相位—高度转换原理如图4所示。

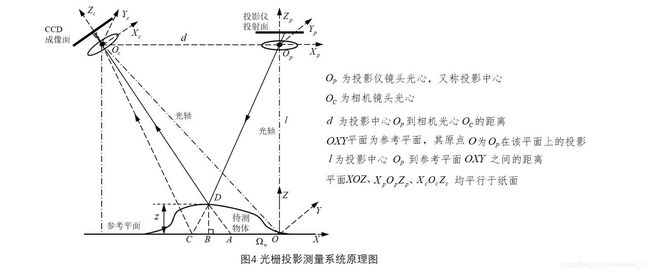
  测量时，投影仪向参考平面 XOY 投射一组正弦光栅图案，以投影仪端的任意一束光线 O_pD 为例，其中 D 是待测物体表面上的任意一点，此时反射光线 DO_c 进入相机视野中，其反向延长线与参考平面 XOY 相交于点 A ，根据透视成像原理，物点 D 和参考平面上的点 A 在相机成像平面上的像点是一致的。如果没有物体 D 点的遮挡，光线 O_pD 将抵达参考平面 XOY ，并经 CO_c 进入相机视野，其中 C 为光线 O_pD 与参考平面 XOY 的交点。因此，受物体高度的调制，相机观察到的点从点 C 平移至了点 A ，C 、A 两点的相位则携带了物点 D 高度信息 z 。推导过程如图5：

  图中 l 、T 、d 为测量系统的固有参数（T为光栅图像中光栅条纹的像素周期长度），在实际搭建的测量系统中，很难通过直接测量得到这些参数的精确值，可以通过标定的方法获得这些参数的精确值。标定包括相机标定、投影仪标定及相机和投影仪的立体标定，以后再作介绍。

3. 三维重建

  数字光栅投影技术中有两种常用的三维重构模型，基于几何光路的模型和基于双目视觉的模型。两种模型从不同的角度建立了相位与空间深度之间的转换关系。

3.1 基于几何光路的模型

  2.2小节图4推导出的相位——高度映射公式就是一种传统的基于几何光路的模型。利用该模型时，必须满足以下关系：（1）投影仪光心与相机光心连线严格与参考平面平行；（2）光栅栅线方向严格与投影仪光心和相机光心的连线垂直；（3）参考面上的栅线节距相同。上述三个约束条件在实际搭建的系统中很难保障，因此很少使用传统的基于几何光路的模型进行高度计算。当然，也有不少学者对次进行改进，放宽了约束条件（控制方程法），但是待求参数过多。

3.2 基于双目视觉的模型

该模型将投影仪——相机系统看作为双目相机视觉系统，从相机与投影仪的各自投影关系恢复三维空间坐标。假设待求的三维空间点坐标为[x_w,y_w,z_w]^T,其在相机平面的像素坐标为(x,y)，根据投影关系有：

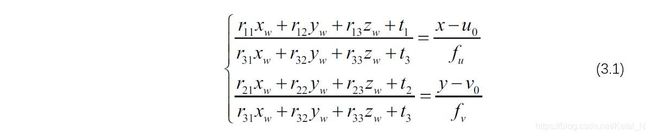
相机经过参数标定后，该方程组将仅剩[x_w,y_w,z_w]^T这三个未知数。假设投影仪投射竖条纹进行相位测量，对于投影仪而言有：

上式中，与投影仪相关的参数用上标p加以区分，（x^p,y^p）为三维点在投影仪上的像素坐标，n_v为投射光栅图案的条纹个数，width为投影仪的宽度方向的像素个数。通过相位解包裹，x^p为已知量，联立式（3.2）（3.3）即可求出[x_w,y_w,z_w]^T。
  三维重建的结果受多重因素影响：系统的标定精度、相位误差、环境噪声等。其中相位误差主要来源于投影仪的gamma非线性，可以对投影仪的gamma非线性进行补偿，提高相位求解质量。投影仪误差补偿主要分主动误差补偿和被动误差补偿，以后再作介绍。

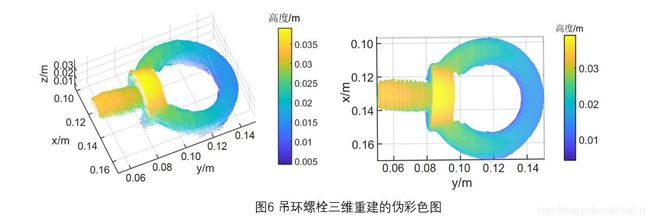
3.3 重建结果

  对吊环螺栓进行了三维重建，结果如图6，重建质量尚可。

【参考文献】

[1] 冯世杰. 基于数字光栅投影的高速实时三维面型测量关键技术研究[D]. 南京：南京理工大学， 2016.
[2] Zuo C, Feng S J, Huang L. Phase shifting algorithms for fringe projection profilometry: A review[J]. Optics and Lasers in Engineering, 2018, 109: 23-59.
[3] Zhang S. High-speed 3D imaging with digital fringe projection techniques[M]. Boca Raton: CRC Press, 2016: 45-70.
ps: 光栅投影三维测量方向，国外推荐普渡大学张松团队，国内四川大学苏显渝团队，东南大学达飞鹏团队，南理工左超团队，华科史玉升团队等。

写在最后

  距上一篇博文已有一年多的时间了。一年，对于整个人生来说不算长，但对处在某些重要时间段的人来说，一年足以影响一生。从小到大，那些“大事件”一直都是出现在报纸、电视、网络上，你看得见它，它看不见你。2020来了，它看见了我，也看到了你，它的影响存在于学习、工作和生活的各个方面。
  去年秋招，很多公司的信息登记表上有这一问：最近一年的愿望是什么？答：顺利毕业，找到一份满意的工作。十个月过去了，时间给出了答案：已毕业，有了一份工作。十个月，经历了很多，告别了学生时代，体会到了个人的渺小、无力，认识到选择的重要性，接受平凡的自己。
  刚毕业的这段时间或许会有些艰难，十年后再回首，可能觉得这些都不算什么吧。最后，前程似锦，未来可期！送给每一位毕业生。