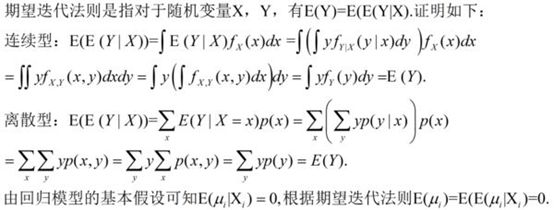常用统计学思维

---

期望迭代法则可以提供一种计算非条件期望的方法。比如这个很经典的计量经济学的例子：员工的性别与平均工资。用虚拟变量X代表员工的性别，其中0代表女性，1代表男性。用Y代表员工的工资水平。那么

---

2 幸存者偏差（Survivorship bias），另译为“生存者偏差”或“存活者偏差”，驳斥的是一种常见的逻辑谬误（“谬误”而不是“偏差”），这个被驳斥的逻辑谬误指的是只能看到经过某种筛选而产生的结果，而没有意识到筛选的过程，因此忽略了被筛选掉的关键信息。这东西的别名有很多，比如“沉默的数据”、“死人不会说话”等等。

3交叉验证（Cross Validation），有的时候也称作循环估计（Rotation Estimation），是一种统计学上将数据样本切割成较小子集的实用方法，该理论是由Seymour Geisser提出的。

在给定的建模样本中，拿出大部分样本进行建模型，留小部分样本用刚建立的模型进行预报，并求这小部分样本的预报误差，记录它们的平方加和。这个过程一直进行，直到所有的样本都被预报了一次而且仅被预报一次。把每个样本的预报误差平方加和，称为PRESS(predicted Error Sum of Squares)。

交叉验证的基本思想是把在某种意义下将原始数据(dataset)进行分组,一部分做为训练集(train set),另一部分做为验证集(validation set or test set),首先用训练集对分类器进行训练,再利用验证集来测试训练得到的模型(model),以此来做为评价分类器的性能指标。

用交叉验证的目的是为了得到可靠稳定的模型。

常用的精度测试方法主要是交叉验证，例如10折交叉验证(10-fold cross validation)，将数据集分成十份，轮流将其中9份做训练1份做验证，10次的结果的均值作为对算法精度的估计，一般还需要进行多次10折交叉验证求均值，例如：10次10折交叉验证，以求更精确一点。

Holdout 验证

常识来说，Holdout 验证并非一种交叉验证，因为数据并没有交叉使用。 随机从最初的样本中选出部分，形成交叉验证数据，而剩余的就当做训练数据。 一般来说，少于原本样本三分之一的数据被选做验证数据。

K-fold cross-validation

K折交叉验证，初始采样分割成K个子样本，一个单独的子样本被保留作为验证模型的数据，其他K-1个样本用来训练。交叉验证重复K次，每个子样本验证一次，平均K次的结果或者使用其它结合方式，最终得到一个单一估测。这个方法的优势在于，同时重复运用随机产生的子样本进行训练和验证，每次的结果验证一次，10折交叉验证是最常用的 [3] 。

留一验证

正如名称所建议， 留一验证（LOOCV）意指只使用原本样本中的一项来当做验证资料， 而剩余的则留下来当做训练资料。 这个步骤一直持续到每个样本都被当做一次验证资料。 事实上，这等同于和K-fold 交叉验证是一样的，其中K为原本样本个数。 在某些情况下是存在有效率的演算法，如使用kernel

regression 和Tikhonov regularization。

4 聚类错觉 是心理学中的一个概念，指人们更倾向于将随机小样本中不可避免的“条纹”或“聚簇”状的随机分布考虑为某种有统计意义的“规律”

---

图中可以看到随机分布的点，但你是否更倾向于注意图中聚拢在一起或者大片没有点的空白区域？这些点的“不正常分布”的区域会吸引你的注意力，甚至让产生原本的随机分布并非随机的错觉。

---

5 维数灾难：通常是指在涉及到向量的计算的问题中，随着维数的增加，计算量呈指数倍增长的一种现象。维数灾难涉及数字分析、抽样、组合、机器学习、数据挖掘和数据库等诸多领域。

当维度增加时，空间的体积增加得很快，使得可用的数据变得稀疏。稀疏性对于任何要求有统计学意义的方法而言都是一个问题，为了获得在统计学上正确并且有可靠的结果，用来支撑这一结果所需要的数据量通常随着维数的提高而呈指数级增长。

6 过度拟合：过拟合是指为了得到一致假设而使假设变得过度严格。避免过拟合是分类器设计中的一个核心任务。通常采用增大数据量和测试样本集的方法对分类器性能进行评价。

定义：给定一个假设空间H，一个假设h属于H，如果存在其他的假设h’属于H,使得在训练样例上h的错误率比h’小，但在整个实例分布上h’比h的错误率小，那么就说假设h过度拟合训练数据。[1]

判断方法：一个假设在训练数据上能够获得比其他假设更好的拟合，但是在训练数据外的数据集上却不能很好地拟合数据，此时认为这个假设出现了过拟合的现象。出现这种现象的主要原因是训练数据中存在噪音或者训练数据太少。

（1）建模样本选取有误，如样本数量太少，选样方法错误，样本标签错误等，导致选取的样本数据不足以代表预定的分类规则；

（2）样本噪音干扰过大，使得机器将部分噪音认为是特征从而扰乱了预设的分类规则；

（3）假设的模型无法合理存在，或者说是假设成立的条件实际并不成立；

（4）参数太多，模型复杂度过高；

（5）对于决策树模型，如果我们对于其生长没有合理的限制，其自由生长有可能使节点只包含单纯的事件数据(event)或非事件数据(no event)，使其虽然可以完美匹配（拟合）训练数据，但是无法适应其他数据集。

解决方法

（2）选取合适的停止训练标准，使对机器的训练在合适的程度；

（3）保留验证数据集，对训练成果进行验证；

（4）获取额外数据进行交叉验证；

（5）正则化，即在进行目标函数或代价函数优化时，在目标函数或代价函数后面加上一个正则项，一般有L1正则与L2正则等。