1、业务了解
辨别乳腺癌肿瘤活体检查结果是良性的还是恶性的
2、数据理解和数据准备
MASS包的biopsy数据集
library(MASS)
data("biopsy")查看数据结构
str(biopsy)
'data.frame': 699 obs. of 11 variables:
V1 : int 5 5 3 6 4 8 1 2 2 4 ...
V3 : int 1 4 1 8 1 10 1 2 1 1 ...
V5 : int 2 7 2 3 2 7 2 2 2 2 ...
V7 : int 3 3 3 3 3 9 3 3 1 2 ...
V9 : int 1 1 1 1 1 1 1 1 5 1 ...
$ class: Factor w/ 2 levels "benign","malignant": 1 1 1 1 1 2 1 1 1 1 ...
head(biopsy)
ID V1 V2 V3 V4 V5 V6 V7 V8 V9 class
1 1000025 5 1 1 1 2 1 3 1 1 benign
2 1002945 5 4 4 5 7 10 3 2 1 benign
3 1015425 3 1 1 1 2 2 3 1 1 benign
4 1016277 6 8 8 1 3 4 3 7 1 benign
5 1017023 4 1 1 3 2 1 3 1 1 benign
6 1017122 8 10 10 8 7 10 9 7 1 malignant
缺失值处理
library(mice)
md.pattern(biopsy)
ID V1 V2 V3 V4 V5 V7 V8 V9 class V6
683 1 1 1 1 1 1 1 1 1 1 1 0
16 1 1 1 1 1 1 1 1 1 1 0 1
0 0 0 0 0 0 0 0 0 0 16 16
16个缺失值,数量较小,可以删除
biopsy.v2 <- na.omit(biopsy)
md.pattern(biopsy.v2)
ID列删除,class列为响应变量,begin=0,malignant=1,创建y列
biopsy.v2 <- biopsy.v2[,-1]
y = ifelse(biopsy.v2$class=="malignant",1,0)
单变量和响应变量关系可视化
library(reshape2)
library(ggplot2)
biop.m <- melt(biopsy.v2,id.vars = "class")
head(biop.m)
class variable value
1 benign V1 5
2 benign V1 5
3 benign V1 3
4 benign V1 6
5 benign V1 4
6 malignant V1 8
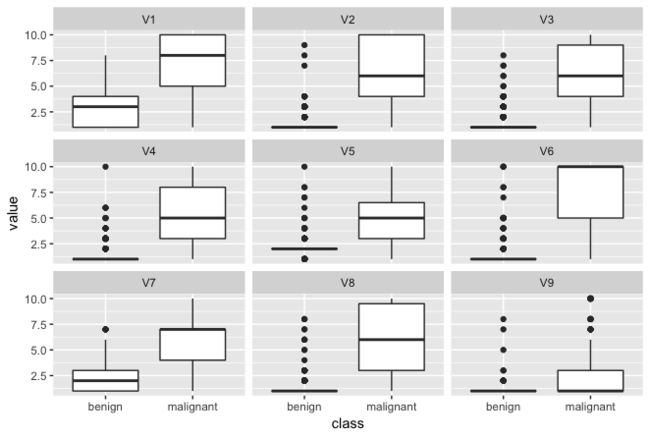
ggplot(data = biop.m,aes(x=class,y=value))+geom_boxplot()+facet_wrap(~ variable,ncol = 3)
从图上看可以得到,早期和晚期相比,特征变量的值总体上小很多。
再做下变量间的相关性分析.。
library(corrplot)
bc <- cor(biopsy.v2[,1:9])
corrplot.mixed(bc)
相关性还是比较强,后面需要留意共线性问题。
划分数据集
set.seed(1234)
ind <- sample(2,nrow(biopsy.v2),replace = TRUE,prob = c(0.7,0.3))
train <- biopsy.v2[ind==1,]
test <- biopsy.v2[ind==2,]
查看是否数据平衡
prop.table(table(train$class))
benign malignant
0.6462 0.3538
prop.table(table(test$class))
benign malignant
0.6588 0.3412
3、建立逻辑回归模型 ------------------------------------------------------------
full.fit <- glm(class~.,family = "binomial",data = train)
summary(full.fit)
Call:
glm(formula = class ~ ., family = "binomial", data = train)
Deviance Residuals:
Min 1Q Median 3Q Max
-3.477 -0.113 -0.057 0.025 2.522
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -10.481 1.510 -6.94 3.8e-12 ***
V1 0.599 0.188 3.18 0.00145 **
V2 -0.151 0.215 -0.70 0.48429
V3 0.371 0.261 1.42 0.15598
V4 0.278 0.144 1.93 0.05360 .
V5 0.172 0.178 0.97 0.33382
V6 0.386 0.108 3.58 0.00034 ***
V7 0.451 0.185 2.43 0.01498 *
V8 0.190 0.119 1.59 0.11098
V9 0.702 0.326 2.15 0.03135 *
Signif. codes: 0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 613.388 on 471 degrees of freedom
Residual deviance: 76.204 on 462 degrees of freedom
AIC: 96.2
Number of Fisher Scoring iterations: 8
多个特征不通过检验,confint()函数可以对模型进行95%的置信区间检验。
confint(full.fit)
Waiting for profiling to be done...
2.5 % 97.5 %
(Intercept) -14.037490 -7.9780
V1 0.263991 1.0127
V2 -0.562948 0.3145
V3 -0.170012 0.8849
V4 -0.002302 0.5760
V5 -0.191308 0.5198
V6 0.182838 0.6107
V7 0.103880 0.8396
V8 -0.038309 0.4353
V9 0.078381 1.2825
先不对特征做筛选处理,算一下VIF统计量。
vif(full.fit)
V1 V2 V3 V4 V5 V6 V7 V8 V9
1.194 2.991 2.953 1.198 1.319 1.225 1.258 1.206 1.084
根据VIF经验法则,共线性不成为这次的问题。
再看下模型在训练数据集和测试集的预测效果。
训练集预测概率
train.probs0 <- predict(full.fit,type = "response")
划分01响应变量训练集和测试集
trainY <- y[ind==1]
testY <- y[ind==2]
混淆矩阵
library(caret)
概率大于等于0.5定义为恶性,小于则良性
train.probs <- ifelse(train.probs0 >= 0.5,1,0)
confusionMatrix(as.factor(trainY),as.factor(train.probs))
Confusion Matrix and Statistics
Reference
Prediction 0 1
0 297 8
1 9 158
Accuracy : 0.964
95% CI : (0.943, 0.979)
No Information Rate : 0.648
P-Value [Acc > NIR] : <2e-16
Kappa : 0.921
Mcnemar's Test P-Value : 1
Sensitivity : 0.971
Specificity : 0.952
Pos Pred Value : 0.974
Neg Pred Value : 0.946
Prevalence : 0.648
Detection Rate : 0.629
Detection Prevalence : 0.646
Balanced Accuracy : 0.961
'Positive' Class : 0
96.4%的正确率。或者用InformationValue包,3.6的错判率。
library(InformationValue)
misClassError(trainY,train.probs)
[1] 0.036
看上去全部特征建立的模型效果非常好,再看看测试集的预测效果。
测试集预测概率
test.probs0 <- predict(full.fit,newdata = test,type = "response")
test.probs <- ifelse(test.probs0 >= 0.5,1,0)
confusionMatrix(testY,test.probs)
0 1
0 137 3
1 2 69
misClassError(testY,test.probs)
[1] 0.0237
4、模型优化
k折交叉验证回归
library(bestglm)
bestglm需要最后一列为响应变量,且为01编码
X <- train[,1:9]
Xy <- cbind(X,trainY)
bestglm(Xy = Xy,IC = "CV",CVArgs = list(Method = "HTF",K=10,REP=1),family = binomial)
Morgan-Tatar search since family is non-gaussian.
CV(K = 10, REP = 1)
BICq equivalent for q in (1.28552625809908e-05, 0.113789358731796)
Best Model:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -8.4659 1.04486 -8.102 5.387e-16
V1 0.7262 0.15886 4.571 4.852e-06
V3 0.7278 0.14910 4.881 1.055e-06
V6 0.5005 0.09764 5.126 2.963e-07
用这三个特征重新建模。
reduce.fit <- glm(class~V1+V3+V6,data = train,family = binomial)
summary(reduce.fit)
Call:
glm(formula = class ~ V1 + V3 + V6, family = binomial, data = train)
Deviance Residuals:
Min 1Q Median 3Q Max
-3.1610 -0.1615 -0.0700 0.0342 2.4210
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -8.4659 1.0449 -8.10 5.4e-16 ***
V1 0.7262 0.1589 4.57 4.9e-06 ***
V3 0.7278 0.1491 4.88 1.1e-06 ***
V6 0.5005 0.0976 5.13 3.0e-07 ***
Signif. codes: 0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 613.39 on 471 degrees of freedom
Residual deviance: 101.94 on 468 degrees of freedom
AIC: 109.9
Number of Fisher Scoring iterations: 7
测试集预测概率
test.cv.probs0 <- predict(reduce.fit,newdata = test,type = "response")
test.cv.probs <- ifelse(test.cv.probs0>=0.5,1,0)
confusionMatrix(testY,test.cv.probs)
0 1
0 136 6
1 3 66
misClassError(testY,test.cv.probs)
[1] 0.0427
效果不及全特征模型,再试试最优子集回归。
bestglm(Xy = Xy,IC = "BIC",family = binomial)
Morgan-Tatar search since family is non-gaussian.
BIC
BICq equivalent for q in (0.487296341372356, 0.546006233805509)
Best Model:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -9.6154 1.2423 -7.740 9.919e-15
V1 0.6243 0.1666 3.748 1.781e-04
V3 0.5121 0.1853 2.764 5.704e-03
V6 0.4108 0.1098 3.741 1.832e-04
V7 0.4647 0.1797 2.586 9.718e-03
V9 0.6566 0.3022 2.172 2.982e-02
结果是5个特征的bic最小,拿这5个特征建模。
bic.fit <- glm(class~V1+V3+V6+V7+V9,family = binomial,data = train)
summary(bic.fit)
Call:
glm(formula = class ~ V1 + V3 + V6 + V7 + V9, family = binomial,
data = train)
Deviance Residuals:
Min 1Q Median 3Q Max
-3.1232 -0.1408 -0.0698 0.0318 2.5578
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -9.615 1.242 -7.74 9.9e-15 ***
V1 0.624 0.167 3.75 0.00018 ***
V3 0.512 0.185 2.76 0.00570 **
V6 0.411 0.110 3.74 0.00018 ***
V7 0.465 0.180 2.59 0.00972 **
V9 0.657 0.302 2.17 0.02982 *
Signif. codes: 0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 613.388 on 471 degrees of freedom
Residual deviance: 85.418 on 466 degrees of freedom
AIC: 97.42
Number of Fisher Scoring iterations: 8
AIC值比三个特征的模型低,算出这个模型在测试集的预测效果。
test.bic.probs0 <- predict(bic.fit,newdata = test,type = "response")
test.bic.probs0 <- predict(bic.fit,newdata = test,type = "response")
test.bic.probs <- ifelse(test.bic.probs0>=0.5,1,0)
confusionMatrix(testY,test.bic.probs)
0 1
0 137 5
1 2 67
misClassError(testY,test.bic.probs)
[1] 0.0332
目前来看,三个模型中全特征模型在测试集的正确率最高,但是部分特征不通过检验,这是得我们陷入选择困境,后面我们可以选择判别分析和多元自适应回归样条方法,看是否能得到更优化的模型。