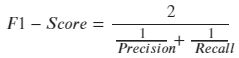广工大数协 阿里云天池 金融风控训练营 - Task1 赛题理解
本学习笔记为阿里云天池龙珠计划Docker训练营的学习内容,学习链接为:https://tianchi.aliyun.com/specials/activity/promotion/aicampdocker
一、学习知识点概要
- 赛题概况
- 数据概况
- 预测指标
- 分析赛题
二、学习内容
2.1 赛题概况
比赛要求参赛选手根据给定的数据集,建立模型,预测金融风险。
赛题以预测金融风险为任务,数据集可下载,该数据来自某信贷平台的贷款记录,总数据量超过120w,包含47列变量信息,其中15列为匿名变量。将从中抽取80万条作为训练集,20万条作为测试集A,20万条作为测试集B,同时会对employmentTitle、purpose、postCode和title等信息进行脱敏。
2.2 数据概况
说明数据中列的性质特征。了解列的性质会有助于我们对于数据的理解和后续分析。
2.3 预测指标
竞赛采用AUC作为评价指标。AUC(Area Under Curve)被定义为 ROC曲线 下与坐标轴围成的面积。
- 分类算法常见的评估指标有:
1.混淆矩阵(Confuse Matrix)
(1)若一个实例是正类,并且被预测为正类,即为真正类TP(True Positive )
(2)若一个实例是正类,但是被预测为负类,即为假负类FN(False Negative )
(3)若一个实例是负类,但是被预测为正类,即为假正类FP(False Positive )
(4)若一个实例是负类,并且被预测为负类,即为真负类TN(True Negative )
2.准确率(Accuracy)
3.精确率(Precision)
又称查准率,正确预测为正样本(TP)占预测为正样本(TP+FP)的百分比。![]()
4.召回率(Recall)
又称为查全率,正确预测为正样本(TP)占正样本(TP+FN)的百分比。![]()
5.F1 Score
精确率和召回率是相互影响的,精确率升高则召回率下降,召回率升高则精确率下降,如果需要兼顾二者,就需要精确率、召回率的结合F1 Score。
6.P-R曲线(Precision-Recall Curve)
P-R曲线是描述精确率和召回率变化的曲线。如下图。
![]()
7.ROC(Receiver Operating Characteristic)
ROC空间将假正例率(FPR)定义为 X 轴,真正例率(TPR)定义为 Y 轴。如下图。
TPR:在所有实际为正例的样本中,被正确地判断为正例之比率。
FPR:在所有实际为负例的样本中,被错误地判断为正例之比率。
![]()
8.AUC(Area Under Curve) AUC(Area Under Curve)
被定义为 ROC曲线 下与坐标轴围成的面积,显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方,所以AUC的取值范围在0.5和1之间。AUC越接近1.0,检测方法真实性越高;等于0.5时,则真实性最低,无应用价值。
-
对于金融风控预测类常见的评估指标有:
1.KS(Kolmogorov-Smirnov)
KS统计量由两位苏联数学家A.N. Kolmogorov和N.V. Smirnov提出。在风控中,KS常用于评估模型区分度。区分度越大,说明模型的风险排序能力(ranking ability)越强。公式如下:
![]()
以下为KS值对应的模型情况,但此对应不是唯一的,只代表大致趋势:
| KS(%) |
好坏区分能力 |
| 20以下 | 不建议采用 |
| 20-40 | 较好 |
| 41-50 | 良好 |
| 51-60 | 很强 |
| 61-75 | 非常强 |
| 75以上 | 过于高,疑似存在问题 |
2.ROC
3.AUC
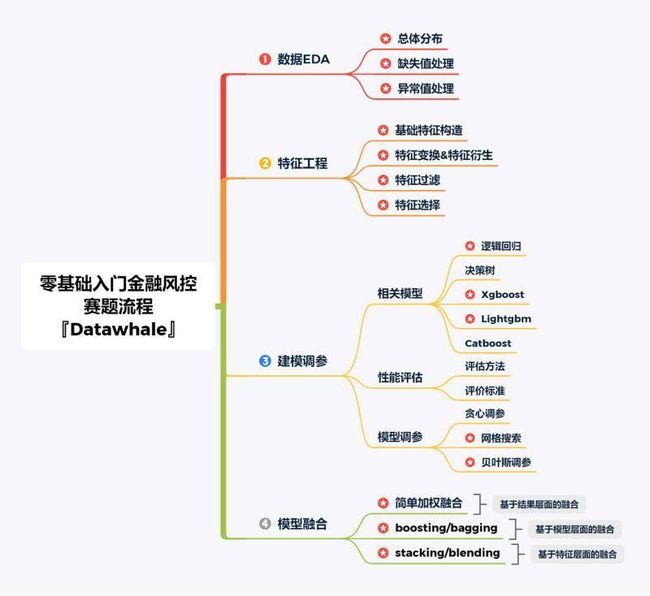
2.4 赛题流程
三、学习问题与解答
1.混淆矩阵的输出结果代表什么意思?
| 0(pred) | 1(pred) | |
| 0(true) | 1对 | 1对 |
| 1(true) | 1对 | 1对 |
2.为什么第一次在执行P-R曲线代码时没有显示图像,下载数据集后就可以显示了?
四、学习思考与总结
1.代码的学习需要一定的数学基础,并不只是死记硬背,首先需要理清其中的逻辑关系,后面模型构建以及代码的编写才能更加顺利。
2.python相对其它程序语言比较简单易学,同时包含了很多图表的类库,有利于对于数据进行可视化处理,非常适合用于数据分析