金融风控数据挖掘-Task1

一、学习知识点概要：

本篇文章主要针对金融风控中分类算法的各个评估指标进行详解，针对阿里云Al训练营金融风控中所讲述的内容，查阅资料并融入自己的见解，编制自己的理解笔记，帮助理解及便于复习。

二、学习内容：

分类算法：

• 何为分类：
  分类(Categorization or Classification)是找出数据库中一组数据对象的共同特点并按照分类模式将其划分为不同的类，其目的是通过分类模型，将数据库中的数据项映射到某个给定的类别。
• 为何要分类：
  当我们拿到一个数据集时，它往往是杂乱无章的，我们需要通过对数据进行分类，更好地提取数据的信息、利用同种类别的数据进行特征分析。
• 如何评价一个分类算法的好坏：
  对于二分类问题，机器预测的和实际的还是会有所偏差，所以我们引入评估指标来评价分类器的优良。

分类算法（分类器）的评估指标：

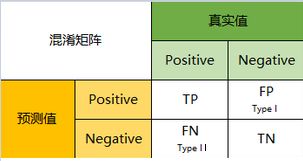
1. 混淆矩阵（一级指标）：混淆矩阵（也称误差矩阵）是评判模型结果的指标，属于模型评估的一部分。如下为混淆矩阵的示意图。¹

• 表格中可以看到两个名词：①真实值：真实值也称实际值，即来自于数据集的值；②预测值：即通过建立模型，由模型预测得到的数值。

• 此外还有四个观测值：
  ①TP（真实正例）：模型预测结果是正例并且实际值也是正例（如预测一名用户违约，而真实中该患者确实违约）
  ②FP（错误正例）：模型预测结果是正例然而实际值确是负例（如预测一名患者违约，而真实中该患者无违约）
  ③FN（错误负例）：模型预测结果是负例然而实际值却是正例（如预测一名患者无违约，而真实中该患者却违约）
  ④TN（真实负例）：模型预测结果是负例并且实际值也是负例（如预测一名患者无违约，而真实中该患者确实无违约）
  （我们在建立模型进行预测时，总希望混淆矩阵中的TP、TN数量越大越好，FP、FN的数量越小越好，这样越能代表模型的预测准确度高）

但是，混淆矩阵里面统计的是个数，有时候面对大量的数据，光凭算个数，很难衡量模型的优劣。因此混淆矩阵在基本的统计结果上又延伸了如下4个二级指标（通过最底层指标加减乘除得到的)。

2. 准确率（Accuracy） ：最直观的理解——正确预测的观测值与总观测值的比率，准确率是常用的一个评价指标，可以衡量所建立的模型预测是否准确，准确率越高，模型预测的准确率越大。但是这一指标不适合样本不均衡的情况。

$$\text{ Accuracy }=\frac{TP+TN}{TP+FP+FN+TN}$$

3. 精确率（Precision）：精确率又称查准率，正确预测为正样本（TP）占预测为正样本(TP+FP)的百分比。意思就是在预测为正样本的结果中，我们有多少把握可以预测正确。同样，我们也希望精确率越高越好。（可以理解为预测的结果准确）

$$\text{Precision}=\frac{TP}{TP+FP}$$

4. 召回率（Recall）：召回率（Recall） 又称为查全率，正确预测为正样本（TP）占正样本(TP+FN)的百分比。

$$\text{Recall}=\frac{TP}{TP+FN}$$

召回率应该结合实例进行分析，如拿银行贷款违约率为例，相对好用户，我们更关心坏用户，不能错放过任何一个坏用户。因为如果我们过多的将坏用户当成好用户，这样后续可能发生的违约金额会远超过好用户偿还的借贷利息金额，造成严重偿失。召回率越高，代表实际坏用户被预测出来的概率越高（此时正例是坏用户、负例是好用户）。它的含义类似：宁可错杀一千，绝不放过一个²。

5. F1-Score：精确率和召回率是相互影响的，精确率升高则召回率下降，召回率升高则精确率下降，如果需要兼顾二者，就需要精确率、召回率的结合F1-Score。

$$F1-\text{ Score }=\frac{2}{\frac{1}{\text{ Precision }}+\frac{1}{\text{ Recall }}}$$

F1-Score指标综合了Precision与Recall的产出的结果。F1-Score的取值范围从0到1，1代表模型的输出最好，0代表模型的输出结果最差

6. P-R曲线：而对于精确率和召回率（查全率）这两者直接的关系，我们还可以引入P-R曲线来描述精确率和召回率的变化

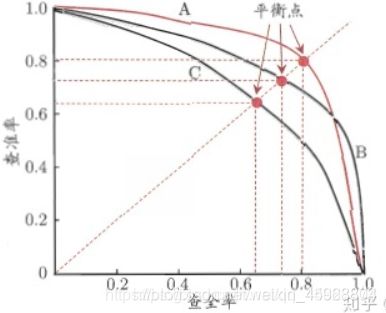
如果我们想要根据一个概率判断用户好坏的话，我们就必须定义一个阈值。在定义的阈值之下，概率大于阈值的为违约用户，反之为诚信用户。而在这个定义的阈值下，我们可以得到相应的一对查准率和查全率。我们希望查准率和查全率同时都非常高。但实际上这两个指标是一对矛盾体，无法做到双高。图中明显看到，如果其中一个非常高，另一个肯定会非常低。选取合适的阈值点要根据实际需求，比如我们想要高的查全率，那么我们就会牺牲一些查准率，在保证查全率最高的情况下，查准率也不那么低。

7. ROC（Receiver Operating Characteristic）
   ROC（接受者操作特征曲线)用于评价模型的预测能力，ROC是一个用于度量分类中的非均衡性的工具，是反映敏感性和特异性连续变量的综合指标，ROC曲线上每个点反映着对同一信号刺激的感受性。想要理解ROC曲线，需要先理解两个变量：FPR和TPR。
   ①FRP（False positive rate）假正率：预测为正但实际为负的样本占所有负例样本的比例。
   $$\text{FRP}=\frac{FP}{FP+TN}$$
   ②TPR（True positive rate）真正率：预测为正且实际为正的样本占所有正例样本的比例。
   $$\text{TRP}=\frac{TP}{TP+FN}$$

在引入了6个指标之后，依然需要引入ROC的意义在于，ROC曲线有一个很好的特征：在实际的数据集中经常会出现类别不平衡现象，即负样本比正样本多很多（或者相反），而且测试数据中的正负样本的分布也可能随着时间而变化。而在这种情况下，ROC曲线能够保持不变。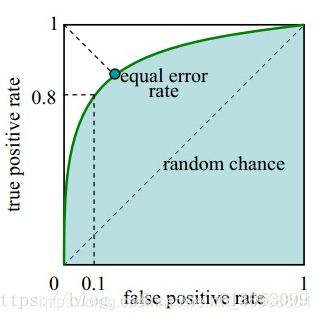

上文中我们有讲述到，我们需要设定一个阈值来判断用户的好坏。对于每一个给定的阈值，对应的可以算出一组（FRP,TRP），在平面中获得对应的坐标点，随着阈值的增大减小，便得到了ROC曲线。阈值最大=1时，对应坐标点（0，0）。阈值最小=0时，对应坐标点（1，1）。对于ROC曲线，我们最希望曲线能够达到点（0,1），此时FRP=0，TRP=1，这会是一个完美的分类器，它将所有样本都正确分类。故ROC曲线越靠拢（0,1）点，越偏离45度对角线越好。

8. AUC(Area Under Curve)
   AUC被定义为 ROC曲线下与坐标轴围成的面积，显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方，所以AUC的取值范围一般在0.5和1之间。使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好，而作为一个数值，对应AUC更大的分类器效果更好。

   从AUC判断分类器（预测模型）优劣的标准³：
   ①AUC = 1，是完美分类器，采用这个预测模型时，存在至少一个阈值能得出完美预测。绝大多数预测的场合，不存在完美分类器。
   ②0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。
   ③AUC = 0.5，跟随机猜测一样（例：丢铜板），模型没有预测价值。
   ④AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测。

9. KS统计量 ： 在金融风控预测中，KS通缉量常用于评估模型区分度。区分度越大，说明模型的风险排序能力（ranking ability）越强。 K-S曲线与ROC曲线类似，不同在于：
   · ROC曲线将真正例率和假正例率作为横纵轴
   · K-S曲线将真正例率和假正例率都作为纵轴，横轴则由选定的阈值来充当。 公式如下：
   $$\text{KS}=max(TPR-FPR)$$
   KS不同代表的不同情况：

KS（%）	好坏区分能力
20以下	不建议采用
20-40	较好
41-50	良好
51-60	很强
61-75	非常强
75以上	过于高，疑似有问题

三、学习问题与解答：

针对上述提到的几个评价指标，我们还可以发现他们并不一定是完全适用的，接下来是对内容提出问题并找寻答案。

• 准确率不适用于样本不均匀的时候

样本分布不均匀指的是不同类别的样本差异非常大，从数据上可以分为大数据分布不均衡（如拥有1000万条记录的数据集中，其中占比50万条的少数分类样本便属于这种情况）和小数据分布不均衡（例如拥有1000条记录的数据集中，其中占有10条样本的分类，其特征无论如何拟合也无法实现完整特征值的覆盖，属于严重的数据样本分布不均衡，）两种情况⁴。这两种情况的出现情景常发生在：
①异常检测场景：例如恶意刷单，黄牛订单，信用卡欺诈，电力窃电，设备故障等，这些数据样本所占比例很小，比如刷实体信用卡的欺诈比例一般在0.1%之内。
②客户流失场景：大型企业的流失客户相对于整体客户而言是少量的，比如电信，石油，网络运营商等行业巨擎。
③罕见事件的分析：如由于某网络大V无意中转发了企业的一条趣味广告导致用户流量明显提升。
④发生频率低的事件：如双十一等活动

• 如何解决样本不均衡问题

①过抽样（over-sampling）：通过增加分类中少数类样本的数量来实现样本均衡，最简单的办法是复制少数类样本形成多条记录，缺点是如果样本特征少会导致过拟合，经过改进的过抽样方法通过在少数类中加入随机噪声，干扰数据或通过一定规则产生新的合成样本，例如SMOTE算法。

②欠抽样（under-sampling）：通过减少分类中多数类样本的数量来实现样本均衡，最直接的办法是随机去掉一些多数类样本来减少多数类的规模，缺点是会丢失多数类样本中的一些重要信息。

③通过组合/集成方法解决样本不均衡（适用于时效性要求不高的模型）
指的是在每次生成训练集时使用所有分类中的小样本量，同时从大样本量中随机抽取数据与小样本量合并构成训练集，反复多次，最后使用组合方法（投票，加权投票）产生分类预测结果。（ 例如数据集中正负例的样本分别为100和10000条，比例1：100，将负样本分为100份，每次形成训练集的时候使用所有的正样本和随机抽取的负样本形成新的数据集，反复进行可得到100个训练集和对应的训练模型。这种思路类似于随机森林。）

这里只讲述其中的三种方法，在文章“机器学习-特征工程中的样本不均衡处理方法”中，讲述了更加详细的方法以及对于特定问题应该选取哪种方法，此处就不再赘述了。

四、学习思考与总结：

在数据挖掘时，没有可以万能套用的模型，也没有可以完美评价模型的指标，我们需要做的是不断扩展自己的知识面，多接触不同的数据类型，多了解一下模型算法，对不同的问题对症下药，找到更好的解决办法！

---

1. 分类模型评判指标 - 混淆矩阵(Confusion Matrix) ↩︎

2. 准确率，精准率，召回率，真正率，假正率，ROC/AUC ↩︎

3. 准确率、精确率、召回率、F1值、ROC/AUC整理笔记 ↩︎

4. 解决样本类别分布不均衡的问题 ↩︎