声明:原创文章,转载请注明出处。https://www.jianshu.com/p/ebe0c98ddf0b
一、概述
遗传算法(Genetic Algorithm)遵循自然界“适者生存、优胜劣汰”的原则,是一类借鉴生物界自然选择和自然遗传机制的随机化搜索算法。
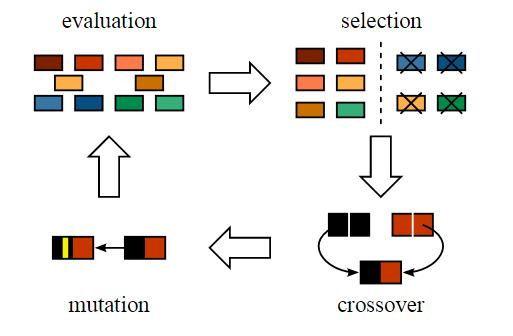
二、算法流程
1、基因编码
对一些个体的基因做一个编码操作,描述出这些基因的结构。
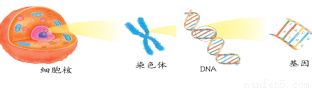
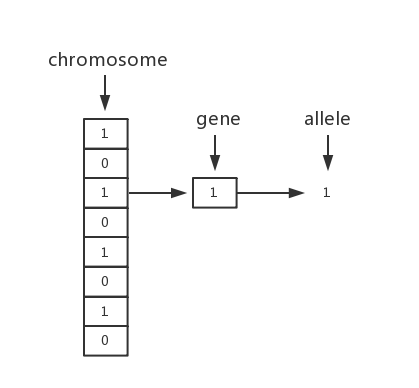
根据常识,在生物的每个细胞中,都存在相同的一套染色体(chromosome),即DNA组合的聚合体。
因此,我们可以将这些染色体由数字0和1组成的字符串来表达。
2、初始化种群
需要造出一个种群,这个种群有多个生物个体,但是其基因却都不相同。
3、种群选择(适应度计算)
需要制造出一些苛刻的条件来淘汰一些不能适应这些条件的个体,不让其产生后代。
这是因为,这些淘汰掉的个体和最终筛选出的个体差异很大,如果保留,他的后代只会让计算量增大而距离目标没有显著增近。
4、产生下一代
这个过程通常有三种方式:直接选择、基因重组(种群交叉)、基因突变(种群变异)。
之后的过程,则会一直重复步骤3-4,直到找到最优解。
三、背包问题
我们通过求解背包问题的最优解来描述遗传算法的步骤。
假设有这样一个背包,可以放置30公斤的东西。现在我们有以下物品,其<重量,价值>有如下关系:
| item | weight | value |
|---|---|---|
| 1 | 15 | 15 |
| 2 | 3 | 7 |
| 3 | 2 | 10 |
| 4 | 5 | 5 |
| 5 | 9 | 8 |
| 6 | 20 | 17 |
怎么能在不超过最大30公斤的限制,选取的物品价值最大呢?
1、基因编码
这6种物品,我们可以采用bit位进行编码。
| item1 | item2 | item3 | item4 | item5 | item6 | chromosome |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 111111 |
共使用6位分别表示是否选取了此Item。1表示选取,0则表示未选取。
假设只有物品1,3,5,则染色体表示为101010。
2、初始化种群
我们随机产生4个生物个体,其染色体如下:
100110:对应物品1,4,5
001110:对应物品3,4,5
010100:对应物品2,4
011001:对应物品2,3,6
3、种群选择
从最初的这4个个体上,我们可以得到如下表格:
| 染色体 | 对应物品 | 总质量 | 总价值 |
|---|---|---|---|
| 100110 | 1,4,5 | 29 | 28 |
| 001110 | 3,4,5 | 16 | 23 |
| 010100 | 2,4 | 8 | 12 |
| 011001 | 2,3,6 | 25 | 34 |
这里我们将总价值这个指标作为染色体的适应度分数,在不超过限制条件的条件下,
其值越大,他的适应性也就越强。
除去苛刻条件的筛选过程(上例是重量超标这个条件),我们还需要一次遴选的过程。即共分为筛选评估和遴选两个过程
我们从总体中选择适合的染色体,让其基因重组,产生下一代。但是这样将会导致染色体在数代之后差异减小,失去了基因的多样性。
一般的,我们会通过轮盘赌这种方式进行选择。
轮盘赌(Roulette Wheel):一种赌博游戏,如下图,可进行旋转。轮盘上刻着很多小格子,轮盘开始旋转后,放入一个小球,待轮盘静止后,小球掉入的所对应的号码即为获胜号码。
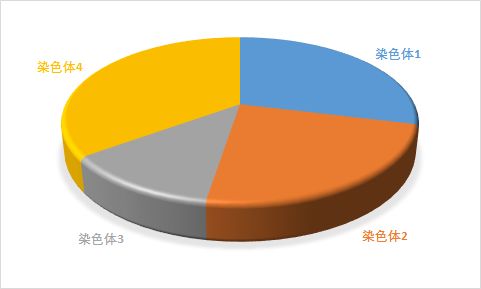
想象一下,在一个分割了97(总适应分数)部分的轮盘,各个染色体的占有率如下:
| 染色体 | 适应分数 | 占有率 |
|---|---|---|
| 100110 | 29 | 28.9% |
| 001110 | 16 | 23.7% |
| 010100 | 8 | 12.4% |
| 011001 | 25 | 35.1% |
我们转动4次,中奖的染色体允许繁殖一次,通过计算染色体1和染色4进入下一轮,各繁殖2次。
将这种方法称为:随机普遍选择法(Stochastic Universal Selection method)。
4、产生下一代
4.1 基因重组
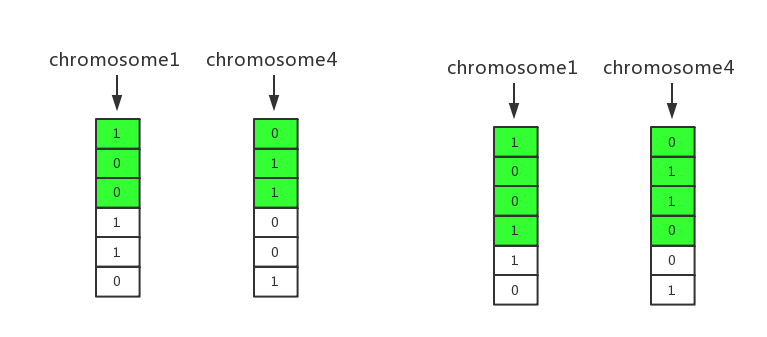
我们将上一步中的染色体1和染色体4进行交叉重组,这里我们选择单点交叉方式。
我们随机选择一个位置,将2个染色体分离并进行重组。
| 个体 | 染色体 | 配对 | 交叉点位置 | 重组结果 |
|---|---|---|---|---|
| 1 | 100 110 | 1-2 | 3 | 100 001 |
| 2 | 011 001 | 1-2 | 3 | 011 110 |
| 3 | 1001 10 | 3-4 | 4 | 1001 01 |
| 4 | 0110 01 | 3-4 | 4 | 0110 10 |
其基因重组过程为下表:
| 个体 | 染色体 | 配对 | 交叉点位置 | 重组结果 |
|---|---|---|---|---|
| 1 | 100 110 | 1-2 | 3 | 100 001 |
| 2 | 011 001 | 1-2 | 3 | 011 110 |
| 3 | 1001 10 | 3-4 | 4 | 1001 01 |
| 4 | 0110 01 | 3-4 | 4 | 0110 10 |
4.2 基因变异
在后代的生长过程中,它们体内的基因会发生一些变化,使得它们与父母不同。这个过程我们称为“变异”,它可以被定义为染色体上发生的随机变化,正是因为变异,种群中才会存在多样性。
变异完成后,即得到了新为个体,进化也就完成了,整个过程如下图:
在生产完下一代之后,我们仍然需要对这些后代进行适应度计算。如果发现出现了连续几代适应度几乎不增加甚至反而减少的情况,
说明函数已经收敛。
因此,一般的,有以下几个终止条件:
- 在进行N次迭代之后,总体适应度没有太大变化。
- 算法事先定义好了进化的次数。
- 适应度函数已经达到了预先设定的值。
四、算法可调参数
1、初始群体
上面的背包问题,我们设定了初始群体个数为4个。当然,针对这6个物品,最多有2^6个个体。一般情况下,我们可以设定初始群体数量为N个,N为当前计算机最大可并行计算数量。
2、适应度函数
上面例子中,我们使用轮盘赌算法。当然也可以选择其他方法。
3、基因重组
上面例子中,我们设定的交叉点为3和4,当然可以选择其他的交叉点。
4、终止条件
上面曾列举了常见的3中终止条件,当然还有其他,目的都是当适应函数收敛后终止。