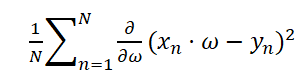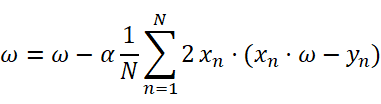pytorch学习（二）：梯度下降算法

优化问题：即求loss最小值。

Gradient：

Update：         其中，α称为学习率。（采用贪心策略）

 

在神经网络中，局部最优点比较小，但是会存在很多的鞍点，即g=0，此时就很难再进行迭代。因此，鞍点是深度学习当中最需要解决的难点。

 

其中，由于：

Gradient：  = 

                   =    

                   =          

                   =          

 

∴Update：

                          

平均梯度下降：

import numpy  as np
import matplotlib.pyplot as plt


x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]

w = 1.0   #初始权重预测

def forward(x):
        return x * w

def cost(xs,ys):
    cost = 0
    for x,y in zip(xs,ys):
        y_pred = forward(x)
        cost += (y_pred - y) **2
    return cost/len(xs)


def gradient(xs,ys):
    grad = 0
    for x,y in zip(xs,ys):
        grad += 2 * x * (x * w - y)
    return grad / len(xs)


print('Predict (before training)',4,forward(4))

epoch_list = []
cost_list = []


for epoch in range(100):
    cost_val = cost(x_data,y_data)
    grad_val = gradient(x_data,y_data)
    w -= 0.01*grad_val       #这里的学习率设置成 0.01.
    print('Epoch:',epoch,'w=',w,'loss=',cost_val)
    epoch_list.append(epoch)
    cost_list.append(cost_val)

print('Predict (after training)',4,forward(4))



plt.plot(epoch_list,cost_list)
plt.ylabel('Loss')
plt.xlabel('epoch')
plt.show()

 

 

随机梯度下降算法的Update为：      其中，α称为学习率。（采用贪心策略）

                                对应的Loss Function：

 

#随机梯度下降算法
import numpy  as np
import matplotlib.pyplot as plt


x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]

w = 1.0   #初始权重预测

def forward(x):
        return x * w

def loss(xs,ys):    #这里变换成loss，可去掉原先的cost = 0
      y_pred = forward(x)
      return  (y_pred - ys) **2


def gradient(xs,ys):
    return 2 * xs *(xs * w - ys)



print('Predict (before training)',4,forward(4))

epoch_list = []
loss_list = []


for epoch in range(100):
    for x,y in zip(x_data,y_data):
        grad_val = gradient(x,y)
        w -= 0.01*grad_val
        print('\tgrad:',x,y,grad_val)
        l = loss(x,y)

    print('progress:',epoch,'w=',w,'loss=',l)
    epoch_list.append(epoch)
    loss_list.append(l)

print('Predict (after training)',4,forward(4))



plt.plot(epoch_list,loss_list)
plt.ylabel('Loss')
plt.xlabel('epoch')
plt.show()

 

 

 

之后会采用Batch_size来平衡时间和性能之间的关系。