机器学习实战笔记-利用SVD简化数据

14.1 SVD的应用

奇异值分解
优点：简化数据，去除嗓声，提高算法的结果。
缺点：数据的转换可能难以理解。
适用数据类型：数值型数据。

14.1.1 隐性语义索引

SVD的历史巳经超过上百个年头，但是最近几十年随着计算机的使用，我们发现了其更多的使用价值。最早的SVD应用之一就是信息检索。我们称利用SVD的方法为隐性语义索引（Latent Semantic Indexing, LSI) 或隐性语义分析（LatentSemanticAnalysis, LSA)。
在LSI中，一个矩阵是由文档和词语组成的。当我们在该矩阵上应用SVD时，就会构建出多个奇异值。这些奇异值代表了文档中的概念或主题，这一特点可以用于更高效的文档搜索。在词语拼写错误时，只基于词语存在与否的简单搜索方法会遇到问题。简单搜索的另一个问题就是同义词的使用。这就是说，当我们查找一个词时，其同义词所在的文档可能并不会匹配上。如果我们从上千篇相似的文档中抽取出概念，那么同义词就会映射为同一概念。

14.1.2 推荐系统

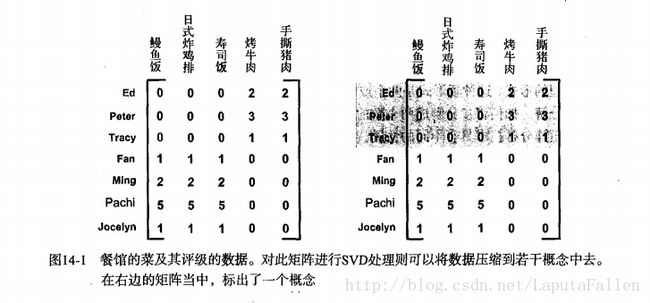
SVD的另一个应用就是推荐系统。简单版本的推荐系统能够计算项或者人之间的相似度。更先进的方法则先利用SVD从数据中构建一个主题空间，然后再在该空间下计算其相似度。考虑图14-1中给出的矩阵，它是由餐馆的菜和品菜师对这些菜的意见构成的。品菜师可以采用1到5之间的任意一个整数来对菜评级。如果品菜师没有尝过某道菜，则评级为0。

我们对上述矩阵进行SVD处理，会得到两个奇异值。因此，就会仿佛有两个概念或主题与此数据集相关联。我们看看能否通过观察图中的0来找到这个矩阵的具体概念。观察一下右图的阴影部分，看起来Ed、Peter和Tracy对“烤牛肉”和 “手撕猪肉”进行了评级，同时这三人未对其他菜评级。烤牛肉和手撕猪肉都是美式烧烤餐馆才有的菜，其他菜则在日式餐馆才有。

我们可以把奇异值想象成一个新空间。与图14-1中的矩阵给出的五维或者七维不同，我们最终的矩阵只有二维。那么这二维分别是什么呢？它们能告诉我们数据的什么信息？这二维分别对应图中给出的两个组，右图中已经标示出了其中的一个组。我们可以基于每个组的共同特征来命名这二维，比如我们得到的美式BBQ和日式食品这二维。

14.2 矩阵分解

在很多情况下，数据中的一小段携带了数据集中的大部分信息，其他信息则要么是噪声，要么就是毫不相关的信息。在线性代数中还有很多矩阵分解技术。矩阵分解可以将原始矩阵表示成新的易于处理的形式，这种新形式是两个或多个矩阵的乘积。我们可以将这种分解过程想象成代数中的因子分解。如何将12分解成两个数的乘积？ (1,12), (2，6)和(3，4)都是合理的答案。
不同的矩阵分解技术具有不同的性质，其中有些更适合于某个应用，有些则更适合于其他应用 。最常见的一种矩阵分解技术就是SVD。SVD将原始的数据集矩阵 Data 分解成三个矩阵 U、∑和VT 。如果原始矩阵 Data 是m行n列 ，那么 U、∑和VT 就分别是m行m列、m行n列和n行n列。为了清晰起见，上述过程可以写成如下一行（下标为矩阵维数)：

Datam∗n=Um∗m∑m∗nVTn∗n

上述分解中会构建出一个矩阵 ∑ , 该矩阵只有对角元素，其他元素均为0。另一个惯例就是， ∑ 的对角元素是 从大到小排列的。 这些对角元素称为奇异值(Singular Value)，它们对应了原始数据集矩阵 Data 的奇异值。回想上一章的PCA，我们得到的是矩阵的特征值，它们告诉我们数据集中的重要特征。 ∑ 中的奇异值也是如此。奇异值和特征值是有关系的。这里的奇异值就是矩阵 Data∗DataT 特征值的平方根。

前面提到过，矩阵 ∑ 只有从大到小排列的对角元素。在科学和工程中，一直存在这样一个普遍事实：在某个奇异值的数目（r个 ）之后，其他的奇异值都置为0。这就意味着数据集中仅有r个重要特征，而其余特征则都是噪声或冗余特征。

14.3 利用Python实现SVD

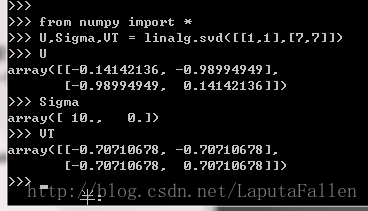
Numpy有 一 个称为linalg的线性代数工具箱。接下来，我们了解一下如何利用该工具箱实现如下矩阵的SVD处理 ：

[1117]

测试代码如下:

我 们注意到，矩阵Sigma以行向量array=([10.,.0.]) 返回，而 非 如 下 矩 阵：

由于矩阵除了对角元素其他均为0，因此这种仅返回对角元素的方式能够节省空间，这就是由Numpy的内部机制产生的。我们所要记住的是，一旦看到Sigma就要知道它是一个矩阵。好了,接下来我们将在一个更大的数据集上进行更多的分解。

建立一个新文件svdRec.py,并加人如下代码:

def loadExData():
    return[[1, 1, 1, 0, 0],
           [2, 2, 2, 0, 0],
           [1, 1, 1, 0, 0],
           [5, 5, 5, 0, 0],
           [1, 1, 0, 2, 2],
           [0, 0, 0, 3, 3],
           [0, 0, 0, 1, 1]]

测试代码如下:

前3个数值比其他的值大了很多。于是，我们就可以将最后两个值去掉了。
接下来，我们的原始数据集就可以用如下结果来近似：

Datam∗n=Um∗3∑3∗3VT3∗n

图14-2就是上述近似计算的一个示意图。

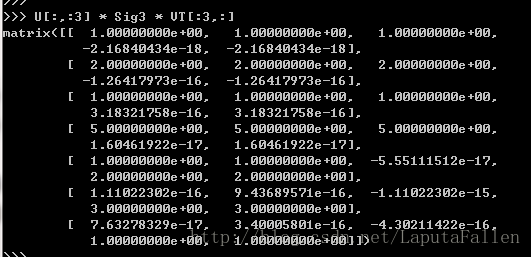
我们试图重构原始矩阵。首先构建一个3X3的矩阵Sig3 ：

接下来我们重构一个原始矩阵的近似矩阵。由于Sig3仅为3X3的矩阵，因而我们只需使用矩阵 U 的前两列和 VT 的前两行。为了在Python中实现这一点，输人如下命令：

我们是如何知道仅需保留前3个奇异值的呢？确定要保留的奇异值的数目有很多启发式的策略 ，其中一个典型的做法就是保留矩阵中90%的能量信息。为了计算总能量信息，我们将所有的奇异值求其平方和。于是可以将奇异值的平方和累加到总值的90%为止。另一个启发式策略就是，当矩阵上有上万的奇异值时，那么就保留前面的2000或3000个 。尽管后一种方法不太优雅，但是在实际中更容易实施。之所以说它不够优雅，就是因为在任何数据集上都不能保证前3000个奇异值就能够包含9 0 %的能量信息。但在通常情况下，使用者往往都对数据有足够的了解，从而就能够做出类似的假设了。
现在我们巳经通过三个矩阵对原始矩阵进行了近似。我们可以用一个小很多的矩阵来示一个大矩阵。有很多应用可以通过SVD来提升性能。下面我们将讨论一个比较流行的SVD应用的例子一推荐引擎 。

14.4 基于协同过滤的推荐引擎

Amazon会根据顾客的购买历史向他们推荐物品，Netflix会向其用户推荐电影，新闻网站会对用户推荐新闻报道，这样的例子还有很多很多。当然，有很多方法可以实现推荐功能，这里我们只使用一种称为协同过滤( collaborative filtering ) 的方法。协同过滤是通过将用户和其他用户的数据进行对比来实现推荐的。

这里的数据是从概念上组织成了类似图14-2所给出的矩阵形式。当数据采用这种方式进行组织时，我们就可以比较用户或物品之间的相似度了。这两种做法都会使用我们很快就介绍到的相似度的概念。当知道了两个用户或两个物品之间的相似度，我们就可以利用已有的数据来预测未知的用户喜好。例如，我们试图对某个用户喜欢的电影进行预测，推荐引擎会发现有一部电影该用户还没看过。然后，它就会计算该电影和用户看过的电影之间的相似度，如果其相似度很高，推荐算法就会认为用户喜欢这部电影。
在上述场景下，唯一所需要的数学方法就是相似度的计算，这并不是很难。接下来，我们首先讨论物品之间的相似度计算，然后讨论在基于物品和基于用户的相似度计算之间的折中。最后，我们介绍推荐引擎成功的度量方法。

14.4.1相似度计算

我们希望拥有一些物品之间相似度的定量方法。那么如何找出这些方法呢？倘若我们面对的是食品销售网站，该如何处理？或许可以根据食品的配料、热量、某个烹调类型的定义或者其他类似的信息进行相似度的计算。现在，假设该网站想把业务拓展到餐具行业，那么会用热量来描述一个叉子吗？问题的关键就在于用于描述食品的属性和描述餐具的属性有所不同。倘若我们使用另外一种比较物品的方法会怎样呢？我们不利用专家所给出的重要属性来描述物品从而计算它们之间的相似度,而是利用用户对它们的意见来计算相似度。这就是协同过滤中所使用的方法。它并不关心物品的描述属性，而是严格地按照许多用户的观点来计算相似度。图14-3给出了由一些用户及其对前面给出的部分菜肴的评级信息所组成的矩阵。

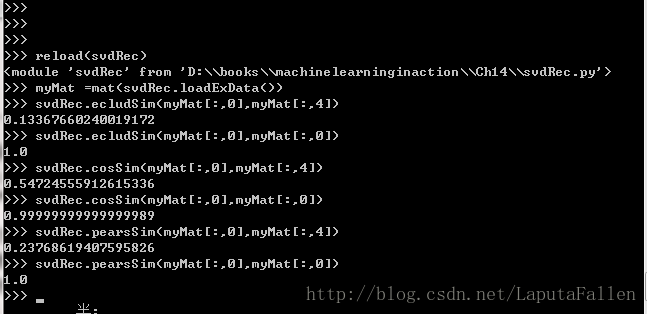
我们计算一下手撕猪肉和烤牛肉之间的相似度。一开始我们使用欧氏距离来计算。手撕猪肉和烤牛肉的欧氏距离为：

(4−4)2+(3−3)2+(2−1)2−−−−−−−−−−−−−−−−−−−−−−−√=1

而手撕猪肉和鳗鱼饭的欧氏距离为：

(4−2)2+(3−5)2+(2−2)2−−−−−−−−−−−−−−−−−−−−−−−√=2.83

在该数据中，由于手撕猪肉和烤牛肉的距离小于手撕猪肉和鳗鱼饭的距离，因此手撕猪肉与烤牛肉比与鳗鱼饭更为相似。我们希望，相似度值在0到1之间变化，并且物品对越相似，它们的相似度值也就越大。我 们可以 用“相似度=1/(1+距离)”这样的算式来计算相似度。当距离为0时，相似度为1.0。如果距离真的非常大时，相似度也就趋近于0。

第二种计算距离的方法是皮尔逊相关系数（Pearson correlation )。我们在第8章度量回归方程的精度时曾经用到过这个量，它度量的是两个向量之间的相似度。该方法相对于欧氏距离的一个优势在于，它对用户评级的量级并不敏感。比如某个狂躁者对所有物品的评分都是5分 ，而另一个忧郁者对所有物品的评分都是1分 ，皮尔逊相关系数会认为这两个向量是相等的。在Numpy中,皮尔逊相关系数的计算是由函数corrcoef()进行的，后面我们很快就会用到它了。皮尔逊相关系数的取值范围从-1到+ 1，我们通过0.5 + 0 . 5 *corrcoef()这个函数计算，并且把其取值范围归一化到0到1之间。

另一个常用的距离计算方法就是余弦相似度（cosine similarity )，其计算的是两个向量夹角的余弦值。如果夹角为90度 ，则相似度为0 ; 如果两个向量的方向相同，则相似度为1.0。同皮尔逊相关系数一样，余弦相似度的取值范围也在-1到+1之间，因此我们也将它归一化到0到1之间。计算余弦相似度值，我们采用的两个向量 A 和 B 夹角的余弦相似度的定义如下：

cosσ=A⋅B||A||||B||

其 中 ，||A||、||B||表示向量A、B的2范数，你可以定义向量的任一范数，但是如果不指定范数阶数，则都假设为2范数。向量[4,2,2]的2范数为：

42+22+22−−−−−−−−−−√

同样，Numpy的线性代数工具箱中提供了范数的计算方法linalg.norm()。

相似度计算，代码如下:

from numpy import *
from numpy import linalg as la

#欧氏距离
def ecludSim(inA,inB):
    return 1.0/(1.0 + la.norm(inA - inB))

#皮尔逊相关系数,注意，用到了归一化
def pearsSim(inA,inB):
    if len(inA) < 3 : return 1.0
    return 0.5+0.5*corrcoef(inA, inB, rowvar = 0)[0][1]

#余弦相似度,注意，用到了归一化
def cosSim(inA,inB):
    num = float(inA.T*inB)
    denom = la.norm(inA)*la.norm(inB)
    return 0.5+0.5*(num/denom)

函数中假定inA和inB都是列向量。pearsSim（）函数会检査是否存在3个或更多的点。如果不存在，该函数返回1.0，这是因为此时两个向量完全相关。

测试代码如下:

上面的相似度计算都是假设数据采用了列向量方式进行表示。如果利用上述函数来计算两个行向量的相似度就会遇到问题（我们很容易对上述函数进行修改以计算行向量之间的相似度)。这里采用列向量的表示方法，暗示着我们将利用基于物品的相似度计算方法。

14.4.2 基于物品的相似度还是基于用户的相似度？

我们计算了两个餐馆菜肴之间的距离，这称为基于物品（item-based)的相似度。另一种计算用户距离的方法则称为基于用户（user-based的相似度。回到图14-3，行与行之间比较的是基于用户的相似度，列与列之间比较的则是基于物品的相似度。到底使用哪一种相似度呢？这取决于用户或物品的数目。基于物品相似度计算的时间会随物品数量的增加而增加，基于用户的相似度计算的时间则会随用户数量的增加而增加。如果我们有一个商店，那么最多会有几千件商品。在撰写本书之际，最大的商店大概有100 000件商品。而在Netflix大赛中，则会有480 000个用户和17 700部电影。如果用户的数目很多，那么我们可能倾向于使用基于物品相似度的计算方法。
对于大部分产品导向的推荐引擎而言，用户的数量往往大于物品的数量，即购买商品的用户数会多于出售的商品种类。

14.4.3 推荐引擎的评价

如何对推荐引擎进行评价呢？此时，我们既没有预测的目标值，也没有用户来调査他们对预测的满意程度。这里我们就可以采用前面多次使用的交叉测试的方法。具体的做法就是，我们将某些已知的评分值去掉，然后对它们进行预测，最后计算预测值和真实值之间的差异。
通常用于推荐引擎评价的指标是称为最小均方根误差（Root Mean Squared Error, RMSE) 的指标，它首先计算均方误差的平均值然后取其平方根。如果评级在1星到5星这个范围内，而我们得到的RMSE为1.0,那么就意味着我们的预测值和用户给出的真实评价相差了一个星级。

14.5 示例：餐馆菜肴推荐引擎

现在我们就开始构建一个推荐引擎，该推荐引擎关注的是餐馆食物的推荐。假设一个人在家决定外出吃饭，但是他并不知道该到哪儿去吃饭，该点什么菜。我们这个推荐系统可以帮他做到这两点。

14.5.1 推荐未尝过的菜肴

推荐系统的工作过程是：给定一个用户，系统会为此用户返回N个最好的推荐菜。为了实现这一点，则需要我们做到：
(1)寻找用户没有评级的菜肴，即在用户- 物品矩阵中的0值 ；
(2)在用户没有评级的所有物品中，对每个物品预计一个可能的评级分数。这就是说，我们认为用户可能会对物品的打分(这就是相似度计算的初衷）；
⑶对这些物品的评分从高到低进行排序，返回前N个物品。

基于物品相似度的推荐引,代码如下:

#dataMat为用户-物品评分矩阵,user为用户列,simMeas为相似度计算函数,item为未评价的物品列号
def standEst(dataMat, user, simMeas, item):
    #得出dataMat的列数，也就是物品数
    n = shape(dataMat)[1]
    #simTotal为相似度总值,ratSimTotal为相似度乘以评分之和
    simTotal = 0.0; ratSimTotal = 0.0
    #迭代物品,找出该用户评分过的物品，求出已评分物品与item(要求的未评分物品)的相似度，累加相似度与评分物品的评分乘积
    for j in range(n):
        userRating = dataMat[user,j]
        #找出用户已评分物品
        if userRating == 0: continue
        #找出已评分物品那一列和未评分物品这一列都被评分过的行(即用户得对两个物品评过分)
        overLap = nonzero(logical_and(dataMat[:,item].A>0, \
                                      dataMat[:,j].A>0))[0]
        #如果overLap为空，那么相似度为0,因为没有用户同时对这两个物品评分                              
        if len(overLap) == 0: similarity = 0
        #算出公共行的相似度，注意用到了数组过滤,simMeas这个相似度计算函数是可以替换的
        else: similarity = simMeas(dataMat[overLap,item], \
                                   dataMat[overLap,j])
        print('the %d and %d similarity is: %f' % (item, j, similarity))
        #累加相似度
        simTotal += similarity
        #累加相似度和评分的乘积
        ratSimTotal += similarity * userRating
    if simTotal == 0: return 0
    #返回计算得到的评分值
    else: return ratSimTotal/simTotal

#为user求出未评分的物品的评分值，从大到小排序
#dataMat为用户-物品评分表,user为用户对应行,simMeas为计算相似度函数,estMethod为求评分的函数
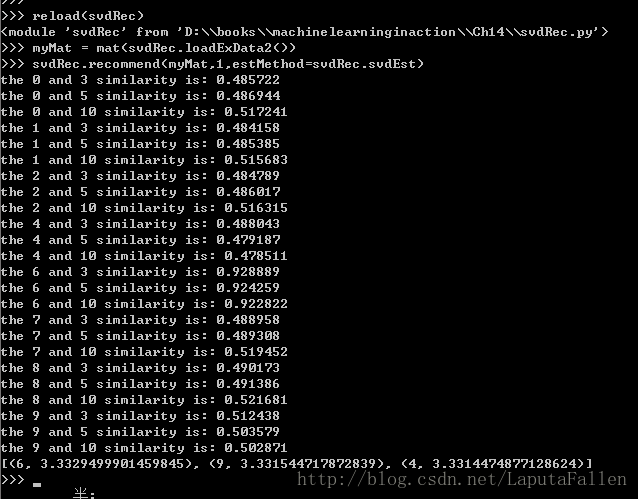
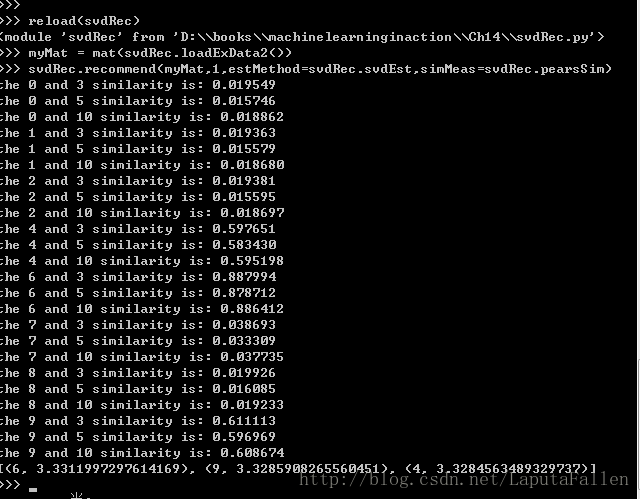
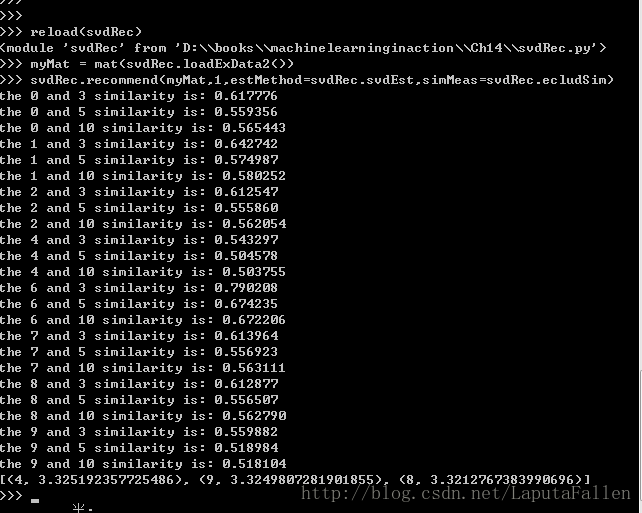
def recommend(dataMat, user, N=3, simMeas=cosSim, estMethod=standEst):
    #找出user对应的未评分的物品的列号，放入unratedItems中
    #find unrated items 
    unratedItems = nonzero(dataMat[user,:].A==0)[1]
    #如果未评分列表为空
    if len(unratedItems) == 0: return 'you rated everything'
    #itemScores存储(物品列数，评分)元组,返回结果为将itemScores按照评分排序后返回
    itemScores = []
    #迭代未评分列表，调用estMethod()返回评分值，将(item,estimatedScore)元组放入itemScores列表中
    for item in unratedItems:
        estimatedScore = estMethod(dataMat, user, simMeas, item)
        itemScores.append((item, estimatedScore))
    #调用sorted()对itemScores按照评分进行排序,通过[:N]数组过滤返回前N个值
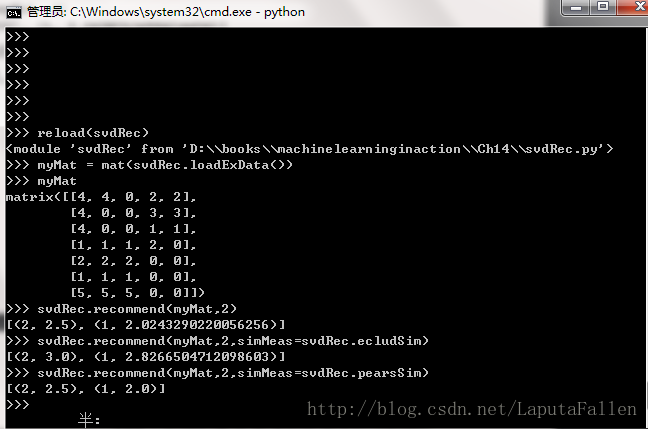
    return sorted(itemScores, key=lambda jj: jj[1], reverse=True)[:N]

笔者测试sorted(itemScores,key=lambda jj:jj[1],reverse=True)[:N],截图如下:

测试截图如下:

14.5.2 利用SVD提高推荐的效果

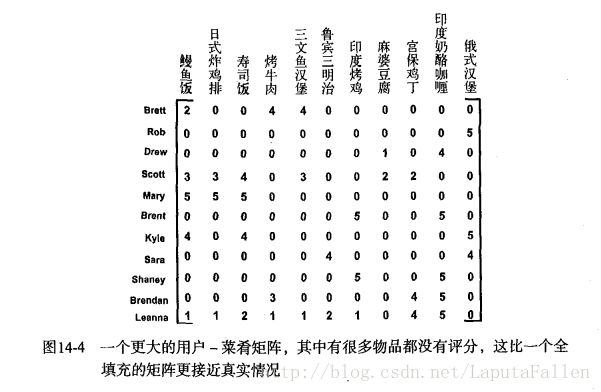
实际的数据集会比我们用于展示recommend()函数功能的myMat矩阵稀疏得多。图14-4就给出了一个更真实的矩阵的例子。

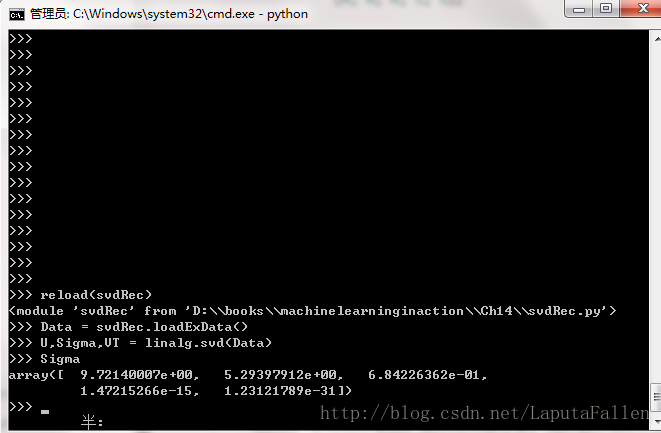
下面我们计算该矩阵的SVD来了解其到底需要多少维特征。代码如下:

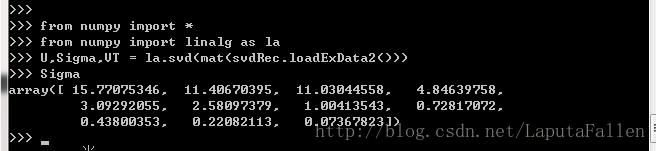
接下来我们看看到底有多少个奇异值能达到总能量的90%。

我们发现,Sigma数组的前三个值之和大于90%。于是，我们可以将一个11维的矩阵转换成一个3维的矩阵。下面对转换后的三维空间构造出一个相似度计算函数。我们利用SVD将所有的菜肴映射到一个低维空间中去。在低维空间下，可以利用前面相同的相似度计算方法来进行推荐。

基于SVD的评分估计,代码如下:

#dataMat为用户-物品评分表,simMeas为相似度计算函数，item未评分物品的列数
def svdEst(dataMat, user, simMeas, item):
    n = shape(dataMat)[1]
    simTotal = 0.0; ratSimTotal = 0.0
    #注意这里调用了la.svd()求出了dataMat的奇异值
    U,Sigma,VT = la.svd(dataMat)
    #将Sigma转换为3*3矩阵，未降维dataMat做准备
    #书中说是3维，但是实际是3维，我这里改了
    #arrange Sig4 into a diagonal matrix
    Sig4 = mat(eye(3)*Sigma[:3]) 
    #利用奇异值和U将dataMat转换为11*3矩阵
    #create transformed items  
    xformedItems = dataMat.T * U[:,:3] * Sig4.I 
    for j in range(n):
        userRating = dataMat[user,j]
        if userRating == 0 or j==item: continue
        #注意这里是xformedItems[item,:]，与之前不同在于两点,一个是利用降维后的xformedItems求相似度，二就是矩阵转置了，所以用[item,:]得出item的评分，注意之后调用了转置，将行向量转换为了列向量
        similarity = simMeas(xformedItems[item,:].T,\
                             xformedItems[j,:].T)
        #print('the %d and %d similarity is: %f' % (item, j, similarity))
        simTotal += similarity
        ratSimTotal += similarity * userRating
    if simTotal == 0: return 0
    else: return ratSimTotal/simTotal

接下来看看程序的执行效果。测试代码如下:

下面再尝试另外一种相似度计算方法：

再换欧式:

我们看到，调用不同的相似度计算函数，结果还是可能不同的。

使用这个数据集调用没有使用SVD分解的commend,测试如下:

import datetime
myMat = mat(loadExData2())
start = datetime.datetime.now().microsecond
recommend(myMat,1)
end = datetime.datetime.now().microsecond
print("start",start)
print("end",end)

start = datetime.datetime.now().microsecond
recommend(myMat,1,estMethod=svdEst)
end = datetime.datetime.now().microsecond
print("start",start)
print("end",end)

测试结果截图如下:

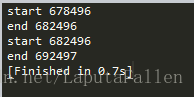
发现用SVD优化的commend还没有不优化快

14.5.3 构建推荐引擎面临的挑战

本节的代码很好地展示出了推荐引擎的工作流程以及SVD将数据映射为重要特征的过程。在撰写这些代码时，我尽量保证它们的可读性，但是并不保证代码的执行效率。一个原因是，我们不必在每次估计评分时都做SVD分解。对于上述数据集，是否包含SVD分解在效率上没有太大的区别。但是在更大规模的数据集上，SVD分解会降低程序的速度。S**VD分解可以在程序调人时运行一次。在大型系统中，SVD每天运行一次或者其运行频率并不高，并且还要离线运行。推荐引擎中还存在其他很多规模扩展性的挑战性问题，比如矩阵的表示方法。在上面给出的例子中有很多0，实际系统中0的数目更多。也许，我们可以通过只存储非零元素来节省内存和计算开销？另一个潜在的计算资源浪费则来自于相似度得分。在我们的程序中，每次需要一个推荐得分时，都要计算多个物品的相似度得分，这些得分记录的是物品之间的相似度。因此在需要时，这些记录可以被另一个用户重复使用。在实际中，另一个普遍的做法就是离线计算并保存相似度得分**。
推荐引擎面临的另一个问题就是如何在缺乏数据时给出好的推荐。这称为冷启动（cold-start )问题，处理起来十分困难。这个问题的另一个说法是，用户不会喜欢一个无效的物品，而用户不喜欢的物品又无效。如果推荐只是一个可有可无的功能，那么上述问题倒也不大。但是如果应用的成功与否和推荐的成功与否密切相关，那么问题就变得相当严重了。
冷启动问题的解决方案，就是将推荐看成是搜索问题。在内部表现上，不同的解决办法虽然有所不同，但是对用户而言却都是透明的。为了将推荐看成是搜索问题，我们可能要使用所需要推荐物品的属性。在餐馆菜肴的例子中,我们可以通过各种标签来标记菜肴，比如素食、美式BBQ、价格很贵等。同时，我们也可以将这些属性作为相似度计算所需要的数据，这被称为基于内容(content-based)的推荐。可能，基于内容的推荐并不如我们前面介绍的基于协同过滤的推荐效果好 ，但我们拥有它，这就是个良好的开始。

14.6 基于SVD的图像压缩

在本节中，我们将会了解一个很好的关于如何将SVD应用于图像压缩的例子。通过可视化的方式，该例子使得我们很容易就能看到SVD对数据近似的效果。在代码库中，我们包含了一张手写的数字图像，该图像在第2章使用过。原始的图像大小是32X32=1024像素，我们能否使用更少的像素来表示这张图呢？如果能对图像进行压缩，那么就可以节省空间或带宽开销了。

图像压缩函数,代码如下:

#输出inMat
def printMat(inMat, thresh=0.8):
    for i in range(32):
        for k in range(32):
            if float(inMat[i,k]) > thresh:
                print('1,',end = "")
            else: print('0,',end = "")
        print('')

#调用imgCompress对img进行压缩
def imgCompress(numSV=3, thresh=0.8):
    myl = []
    for line in open('0_5.txt').readlines():
        newRow = []
        for i in range(32):
            newRow.append(int(line[i]))
        myl.append(newRow)
    myMat = mat(myl)
    print("****original matrix******")
    printMat(myMat, thresh)
    U,Sigma,VT = la.svd(myMat)
    SigRecon = mat(zeros((numSV, numSV)))
    for k in range(numSV):#construct diagonal matrix from vector
        SigRecon[k,k] = Sigma[k]
    #重构img
    reconMat = U[:,:numSV]*SigRecon*VT[:numSV,:]
    print("****reconstructed matrix using %d singular values******" % numSV)
    printMat(reconMat, thresh)

测试代码如下:

测试截图如下:

****original matrix******
0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,1,1,1,1,1,1,1,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,1,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,1,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,0,
0,0,0,0,0,0,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,
0,0,0,0,0,0,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,
0,0,0,0,0,0,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,
0,0,0,0,0,0,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,
0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,
0,0,0,0,0,0,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,
0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,
0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,
0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,
0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,
0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,0,1,1,1,1,1,1,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,1,1,1,1,1,1,0,0,0,0,0,1,1,1,1,1,1,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,
****reconstructed matrix using 2 singular values******
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
[Finished in 0.8s]

可以看到，只需要两个奇异值就能相当精确地对图像实现重构。那么，我们到底需要多少个0-1的 数 字 来 重 构 图 像 呢 ？ U 和 VT 都 是32*2 的 矩 阵 ，有 两 个 奇 异 值 。 因此总数字数目是64+64+2=130。和原数目1024相比，我们获得了几乎10倍的压缩比。

14. 7 本章小结

SVD是一种强大的降维工具，我们可以利用SVD来逼近矩阵并从中提取重要特征。通过保留矩阵80% ~ 90% 的能量，就可以得到重要的特征并去掉噪声。SVD已经运用到了多个应用中，其中一个成功的应用案例就是推荐引擎。
推荐引擎将物品推荐给用户，协同过滤则是一种基于用户喜好或行为数据的推荐的实现方法。协同过滤的核心是相似度计算方法；有很多相似度计算方法都可以用于计算物品或用户之间的相似度。通过在低维空间下计算相似度，SVD提高了推荐系引擎的效果。
在大规模数据集上，SVD的计算和推荐可能是一个很困难的工程问题。通过离线方式来进行SVD分解和相似度计算，是一种减少冗余计算和推荐所需时间的办法。在下一章中，我们将介绍在大数据集上进行机器学习的一些工具。