Python 各种排序算法的比较

一、走进算法的世界

1、什么是算法

人工智能 是当今时代的流行词汇，这也使很多想要在人工智能领域有所成就的大学生选择了计算机类专业。在我们身边，就会有很多人工智能应用的例子。例如，医院里，医生借助 AI 辅助诊断患者是否患有疾病；街道上，公共部门利用机器人喷洒消毒液；高速路上，交警使用无人机巡逻、疏导车辆等。

人工智能 是计算机的一个分支，自然也离不开程序语言，程序语言非常强大(如下图所示)

可以用于 Web 开发、游戏开发、为桌面应用程序构建脚本和 GUI、配置服务器、执行科学计算和进行数据分析等。可以说，程序语言几乎可以用于做任何事情！那么程序语言为何如此强大？这就离不开程序中 精美绝伦 的算法。因此说，一个成功的程序背后必会有一个好的算法。

目前，现代生活已经非常依赖信息技术了，似乎计算机什么都能干，但稍稍了解计算机内部结构的人就会知道，其实计算机只是比较 听话，它并不知道自己在做什么，使用者让它去做什么动作它就会执行什么动作。而能够让计算机系统变得无所不能的是各种各样的算法，如图所示：

人类用智慧设计的算法，造就了计算机的 智能。因此，人类告诉计算机以什么样的顺序去执行某些动作，这就是我们通常说的 算法。

要想在编程之路上走得长远就必须拥有编程思维，那么究竟什么是编程思维？虽然计算机相关的学者至今没有一个明确的定义，但我们可以将编程思维理解成人类的思想方式，而算法是计算机编程思维的一种表现。从当前计算机应用的水平来看，人们已经设计出许多非常 聪明 的算法，极大提高了我们解决问题的能力，但仍有许多复杂问题依然期待人类给出更有效的算法。

2、算法的作用

算法是计算机科学中的核心理论之一，也是人类使用计算机解决问题的技巧之一。算法不仅可以应用在计算机领域中，还可以应用在数学、物理等一些学术领域中，不仅如此，其实在我们的生活中，也是在时时刻刻使用算法。例如，大厨制作美食的过程、制定工作计划、设计精美页面流程等，都在无形中进行着算法操作。本小节将从搜索信息、通信、工业、数学等方面来介绍算法的作用。

2.1 搜索信息方面

当今是大数据覆盖的时代，算法加数据能演化出 五花八门 的应用。例如，我们最熟悉的搜索引擎——百度，如下图所示：

高效的算法让用户能够精准地找到想要搜索的信息，如果没有这些 聪明 的算法，用户将迷失在互联网这个巨大的数据森林中。

2.2 通信方面

算法不仅在搜索信息方面有所成就，在通信方面亦是如此。如果没有天才的编码和加密算法，我们也不可能在网络上安全地通信，天气预报也不能够如此准确。

2.3 工业方面

工业生产需要大量的劳动力来推动生产线的运作。而如何对生产线进行有序管理、保障产品质量、提高生产效率就成为； 工业生产中的重中之重。工业自动化管理系统通过大量精密算法的使用，能够智能地对生产中的各个环节进行管理、监控、优化、完善，如下图所示：

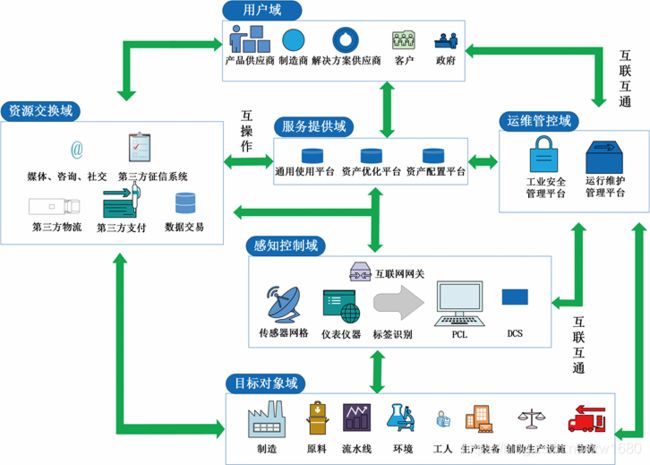
2.4 数学方面

算法领域巨大的进步就是来自于美好的思想，它指引我们更有效地解决数学问题。数学领域的问题并不局限于算术计算，还有很多表面不是数学化的问题，例如：

1. 如何排序
2. 如何找到最短距离
3. 如何走出迷宫
4. 如何解决 千年虫 问题

这些问题非常具有挑战性，需要逻辑推理、几何与组合想象力，才能解决问题，这些就是设计算法所需要的主要能力。

2.5 其他方面

除此之外，工业机器人、汽车、飞机以及几乎所有家用电器中都包含的许多的微处理器都是依赖算法才能发挥作用。例如：飞机中成百上千的微处理器在算法的帮助下控制引擎、减少能耗、降低污染等；微处理器能控制汽车的制动器和方向盘，提高稳定性和安全性；微处理器可以代替人类实现汽车无人驾驶。微处理器的强大背后离不开完美的算法。

所以说，算法很强大，学好算法，你可以编写出健壮的程序，工作中也不会畏惧更加严峻的挑战。

3、算法的基础

许多人认为学习编程就是学习最新的编程语言、技术和框架，其实计算机算法更重要。从 C 语言、C++、Java 到 Python，虽然编程语言种类很多，但是亘古不变的是算法。所以修炼好算法这门 内功，再结合编程语言这些 招式，才能称霸 编程武林。本节就来介绍算法的基础。

3.1 算法的定义

算法是一组完成任务的指令，因此有计算机工作者这样对其进行定义：为了解决某个或某类问题，需要把指令表示成一定的操作序列，操作序列包括一组操作，每一个操作都会完成特定的功能。简单来说，算法是解决特定问题步骤的描述，即处理问题的策略。

例如：经典问题——百钱买百鸡。说明：这篇博文中的分析过程到代码的实现，整个过程就是算法的过程。

3.2 算法的特性

算法是解决 做什么 和 怎么做 的问题，解决一个问题可能有不同的方法，但是算法分析最为核心的是算法的速度。因此解决问题的步骤是需要在有限时间内能够完成的，并且操作步骤中不可以有不明确的语句，使得步骤无法继续进行下去。通过对算法概念的分析，可以总结出一个算法必须满足如下五个特性。如下图所示。本节就来介绍这五大特性。

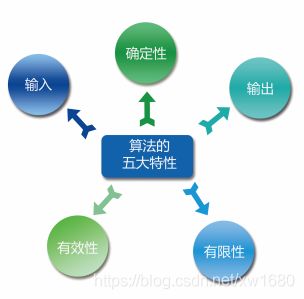
1. 输入。一个程序中的算法和数据是相互联系的，算法中需要输入的是数据的值。输入数据可以是多个，也可以是零个，其实输入零个数据并不表示这个算法没有输入，而是这个输入没有直观地显现出来，隐藏在算法本身当中。例如，Python 语言中用 input() 函数向控制台上输入数据，代码如下：

   name = input("请输入您的姓名:")  # 输入变量值
   

2. 确定性。一个算法中的每一个步骤的表述都应该是确定的。在人们的日常生活中，遇到语意不明确的语句，虽然可以根据常识、语境等理解，但是还有可能理解错误。如下图所示，在中国的社交中，熟人见面经常会问：“吃了没？” 如果是不了解中国文化的外国人就很难理解这句话，这是问吃什么呢？吃饭？吃水果？也不确定这个问句是问谁的。这句话没有确定性，既没有主语，也没有宾语。人遇到这样的问题都很难理解，何况计算机了。计算机不比人脑，不会根据算法的意义来揣测每一个步骤的意思，所以算法的每一步都要有确定的含义。
   

3. 输出。输出就是算法实现所得到的结果。算法没有输出是没有意义的。有的算法输出的是数值；有的输出的是图形，有的输出则不显而易见。例如：

   print("1314")   # 输出数值
   print("^ _ ^")     # 输出图形
   print(" ")      # 输出空格，不显而易见
   

4. 有限性。一个算法在执行有限步骤后能够实现，或者能够在有限时间内完成，就称为该算法具有有限性。例如，在 百钱买百鸡 代码的 for 循环中(1,20)、(1, 33)、(3, 98, 3) 这几个范围，控制了这段程序的有限性。如果没有此条件，for 循环就会无终止地循环，这样程序就进入了死循环，不满足算法的有限性。

   有的算法在理论上满足有限性的，在有限的步骤后能够完成，但是实际上计算机可能会执行一天、一年、十年、甚至更久的时间。算法的核心就是速度，那么这个算法也就没有意义了。总而言之，有限性没有特定的限度，主要取决于使用者的需要。

5. 有效性。算法的有效性就是指每一个步骤都能够有效地执行，并且得到确定的结果，还能够用来方便地解决一类问题。例如：下面这段程序代码中的 z=x/y 就是一个无效的语句，因为 0 是不可以作为分母的。
   

3.3 算法性能分析与度量

算法是解决问题的方法。但是解决问题的方法不止一个，方法多了，自然而然就有了优劣之分。例如，当一个人在扫地的时候，人们不会发现这个人扫地的好与坏。然而，有两三个人同时做这个工作的时候，人们就有了比较，就可以根据不同的评定标准评价工作的优劣。有人认为 A 好，因为他扫得快；有人认为 B 好，因为他扫得干净等。

那么，对于算法的优劣怎么来评定呢？下面就从算法的性能指标和算法效率的度量这两个方面来介绍。

算法的性能指标

评定一个算法的优劣，主要有以下几个指标：

1. 正确性：一个算法必须正确才有存在的意义，这是最重要的指标，要求编程人员应用正确的计算机语言实现算法的功能。
2. 友好性：算法实现的功能是给用户使用的，自然要具有良好的使用性，即用户友好性。
3. 可读性：算法的实现可能需要多次的修改，也可能被移植到其他的功能中，因此算法应当是可读的、可以理解的，方便程序人员对其分析、修改移植到自己的程序中实现某些功能。
4. 健壮性：在算法中经常出现不合理的数据或者非法的操作，所以一个算法必须具有健壮性才能够对这些问题进行检查、纠正。当我们刚开始学习写算法的时候可以忽略健壮性的存在，但是必须通过不断地学习努力让算法更加完美。
5. 效率：算法的效率主要是指执行算法时计算机资源的消耗。包括计算机内存的消耗和计算机运行时间的消耗。两者可以统称为时空效率。一个算法只有正确性而无效率是没有意义的，通常，效率也可以评定一个算法是否正确。如果一个算法需要执行几年，甚至几百年，那么这个算法会被评为是错误的。

算法效率的度量

度量算法效率的方法有两种：

第一，事后计算。先实现算法，然后运行程序并测算其时间和空间的消耗。这种度量方法有很多弊端，由于算法的运行与计算机的软件、硬件等环境因素有关，不容易发现算法本身的优劣。同样的算法用不同的编译器编译出的目标代码不一样多，完成算法所需的时间也不同，并且当计算机的存储空间小时，算法运行时间就会延长。

第二，事前分析估算。这种度量方法是通过比较算法的复杂性来评价算法的优劣，算法的复杂性与计算机软硬件无关，仅与计算时间和存储需求有关。算法复杂性的度量可以分为 空间复杂度度量 和 时间复杂度度量。

算法的时间复杂度

算法的时间复杂度度量主要是计算一个算法所用的时间，主要包括程序编译时间和运行时间。由于一个算法一旦编译成功可以多次运行，因此忽略编译时间，在这里只讨论算法的运行时间。

算法的运行时间依赖于加、减、乘、除等基本的运算，以及参加运算的数据大小、计算机硬件和操作环境等。所以要想准确地计算时间是不可行的，我们可以通过计算影响算法运行时间作为主要的因素：问题的规模，也就是输入量的多少，来计算算法的时间复杂度。

同等条件下，问题的规模越大运行的时间也就越长。例如，求 1+2+3+…+n 的算法，即 n 个整数的累加求和，这个问题的规模为 n。因此，运行算法所需的时间 T 是问题规模 n 的函数，记作 T(n)。

为了客观地反映一个算法的执行时间，通常用算法中基本语句的执行次数来度量算法的工作量。而这种度量时间复杂度的方法得出的不是时间量，而是一种增长趋势的度量。当 n 不断变化时，T(n) 也会不断变化。但有时我们想知道它变化时将呈现什么规律。为此，我们引入时间复杂度概念。一般情况下，算法中基本操作重复执行的次数是问题规模 n 的某个函数，用 T(n) 表示，若有某个辅助函数 f(n)，使得当 n 趋近于无穷大时，T(n)/f(n) 的极限值为不等于零的常数，则称 f(n) 是 T(n) 的同数量级函数。记作 T(n)=O(f(n))，称 O(f(n)) 为算法的渐进时间复杂度，这种 O(f(n)) 表示法被称为大O(大写的字母O)表示法。

算法的空间复杂度

算法的空间复杂度是指在算法的执行过程中，需要的辅助空间数量。辅助空间数量指的不是程序指令、常数、指针等所需要的存储空间，也不是输入数据所占用的存储空间。辅助空间是除算法本身和输入输出数据所占据的空间以外的算法临时开辟的存储空间。算法的空间复杂度分析方法同算法的时间复杂度相似，设 S(n) 是算法的空间复杂度，通常可以表示为：

S(n) = 0(f(n))

例如：当一个算法的空间复杂度为一个常量，即不随被处理数据量 n 的大小而改变时，可表示为 O(1)；当一个算法的空间复杂度与以 2 为底的 n 的对数成正比时，可表示为 O(log2n)；当一个算法的空间复杂度与 n 成线性比例关系时，可表示为O(n)。

4、大 O 表示法

4.1 概念与举例

概念。大O表示法是一种特殊的表示法，它表示算法的时间复杂度(即速度)。说明：大O表示法是对算法性能的一种粗略估计，并不能精准地反映某个算法的性能。

举例。看到这里，大家可能存在疑惑，大O表示法是怎么表示的？接下来我们用一个程序介绍大O表示法是怎样表示该程序的时间复杂度(请读者用函数的角度思考以下讲解内容)。

【实例1】计算 a、b、c 的值。例如：a+b+c=1000 且 a²+b²=c²(a、b、c 都是自然数)，求 a、b、c 的可能组合(a、b、c 的范围在 0~1000 之间)。代码如下：

import time

start_time = time.time()
# 注意是三重循环
for a in range(0, 1001):  # 遍历a
    for b in range(0, 1001):  # 遍历b
        for c in range(0, 1001):  # # 遍历c
            if a ** 2 + b ** 2 == c ** 2 and a + b + c == 1000:  # 条件
                print("a, b, c: %d, %d, %d" % (a, b, c))
end_time = time.time()
print("elapsed: %f" % (end_time - start_time))
print("complete!")

最终需要大约 532 秒(不同计算机的运行时间不同)之后才能运行出结果，结果如下图所示：

将这段代码的进行如下修改：

import time

start_time = time.time()
# 注意是三重循环
for a in range(0, 1001):  # 遍历a
    for b in range(0, 1001):  # 遍历b
        c = 1000 - a - b  # 用表达式求解c
        if a ** 2 + b ** 2 == c ** 2 and a + b + c == 1000:  # 条件
            print("a, b, c: %d, %d, %d" % (a, b, c))
end_time = time.time()
print("elapsed: %f" % (end_time - start_time))
print("complete!")

第二段代码最终运行的结果所需的时间不到 1 秒钟，结果依然是上图所示的内容。从速度上看，第二段代码更快，也就是说，第二段代码算法要比第一段代码算法更成熟，意义上更好一些。那接下来从时间上分析一下这两段代码：

1. 第一段代码的时间复杂度：设时间为 f，这段代码用到了 3 个 for 循环，每个循环遍历一次运行的时间复杂度是 1000，3 次嵌套 for 循环的时间复杂度是每层 for 循环时间复杂度相乘，即 T=1000*1000*1000。而 for 循环之后的 if 和 print() 两条语句，我们暂且算成是2。因此这段程序的时间复杂度是：

   f = 1000 * 1000 * 1000 * 2
   

   如果将 for 循环的范围写成 0~n，那么时间复杂度就变成了一个函数，其中 n 是一个变量，可以写成如下形式，也等价于 f(n)=n³*2：
   
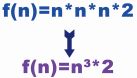
   f(n)=n³*2 函数在象限图的分布如下图所示：
   
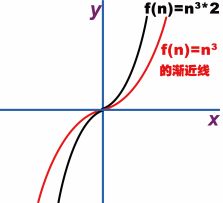
   从图像可以看到，这个函数的走势是不变的，而系数无论是 2 还是1，只不过是使这个走势更陡峭一些，并不影响大趋势，因此可以忽略系数 2。那么图像所示的走势基本可以说是 f(n)=n³ 的象限图，增加的系数形成的象限图只不过是f(n)=n³ 的渐近线(如上图所示的红色线)，对应的函数就是渐近函数，将一系列表示时间复杂度的渐近函数用 T(n) 来表示，就变成了如下形式(k 表示系数)：
   
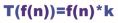
   前面提过，系数 k 并不影响函数走势，所以这里可以忽略 k 的值，最终 T(n) 可以写成如下形式：
   
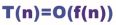
   这种形式就是大 O 表示法，f(n) 是 T(n) 的 大O 表示法。其中的 O(f(n)) 就是这段代码的渐近函数的时间复杂度，简称时间复杂度，也就是 T(n)。通过上面对算法时间复杂度的分析，总结出这样一条结论，在计算任何算法的时间复杂度时，可以忽略所有低次幂和最高次幂的系数，这样可以简化算法分析，并使注意力集中在增长率上。

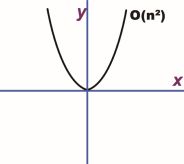
2. 第二段代码的时间复杂度：第二段代码有 2 层 for 循环，忽略系数，它的时间复杂度就是 T(n)=n²，最终的时间复杂度 f(n)=O(n²)，这段代码的复杂度的走势如下图所示：
   

例如：这样一段代码：

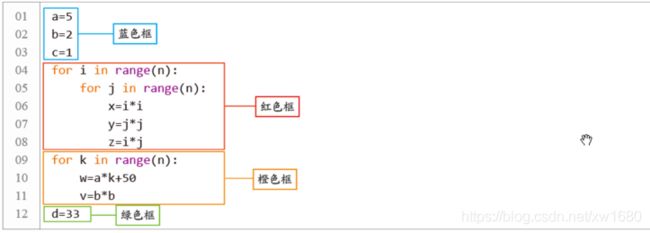
求这段代码的时间复杂度 T(n)，分析如下：

1. 蓝色的时间复杂度是 T1(n)=3 (3条语句)
2. 红色的时间复杂度是 T2(n)=n*n*3=n²*3（2层 for 嵌套循环乘以 3 条语句）
3. 橙色的时间复杂度是 T3(n)=n*2（1层 for 循环乘以 2 条语句）
4. 绿色的时间复杂度是 T4(n)=1（1条语句）
5. 这段程序的时间复杂度是 T(n)= T1(n)+ T2(n)+ T3(n)+ T4(n)= 3+n²*3+n*2+1= n²*3+n*2+4

根据大O表示法推导形式(忽略所有低次幂和最高次幂的系数，包括常数)，最终的大O表示法是 T(n)=O(n2)。象限图和上图所示的一样。 常见的几个大O表示法如下：

二、各种排序算法的比较

1. Python 编程1000例(21)：排序算法——选择排序法
2. Python 编程1000例(21)：排序算法——冒泡排序法
3. Python 编程1000例(21)：排序算法——直接插入排序法
4. Python 编程1000例(21)：排序算法——合并排序法
5. Python 编程1000例(21)：排序算法——希尔排序法
6. Python 编程1000例(21)：排序算法——快速排序法
7. Python 编程1000例(21)：排序算法——堆排序法
8. Python 编程1000例(21)：排序算法——计数排序法
9. Python 编程1000例(21)：排序算法——基数排序法

在之前的博文中一共介绍了 9 种排序算法，那么这 9 种排序算法的各种复杂度是怎样的呢？本节就来总结各种算法的复杂度以及稳定情况。

说明：假设需要排序的数列长度为 n，各种排序算法复杂度如下表所示：

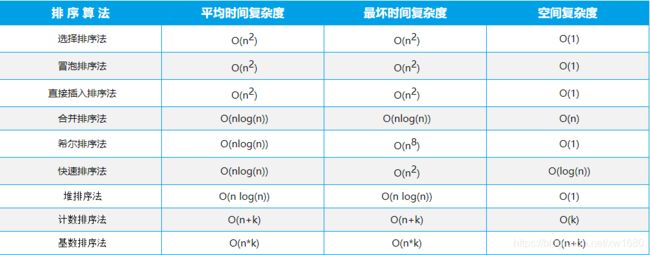
多学两招：辅助记忆法：冒泡、选择、直接排序需要两个 for 循环，每次只关注一个元素，平均时间复杂度为 O(n2)(一遍找元素O(n)，一遍找位置O(n))。快速、合并、希尔基于二分思想，平均时间复杂度为 O(nlog(n))(一遍找元素O(n)，一遍找位置O(logn))。计数排序、基数排序是线性阶(O(n))排序。