数位dp

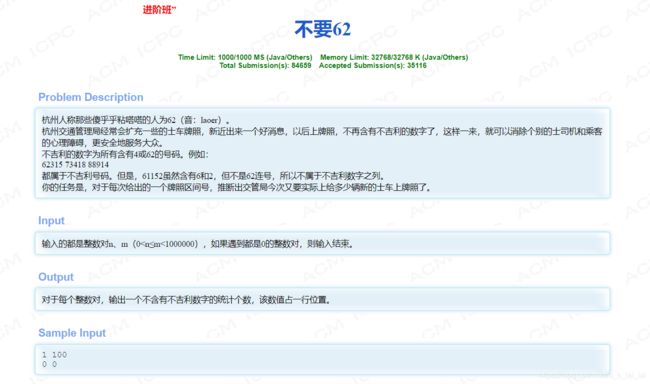
1. 不要62（数位dp）

题目链接

#include 
#include 
#include 
#include 
using namespace std;
typedef long long ll;
int a[20];
int dp[20][2];
int dfs(int pos, int pre, int sta, bool limit) {
     
    //limit是表示前一位是否为上限位
    //pos表示当前位
    //pre表示前一位
    //sta表示前一位是否为题目限制敏感数（这题是6）
    if (pos == -1)
        return 1;
    if (!limit && dp[pos][sta] != -1)
        return dp[pos][sta];
    int up = limit ? a[pos] : 9;
    int tmp = 0;
    for (int i = 0; i <= up; i++) {
     
        if (pre == 6 && i == 2)
            continue;
        if (i == 4)
            continue;  //都是保证枚举合法性
        tmp += dfs(pos - 1, i, i == 6, limit && i == a[pos]);
    }
    if (!limit)
        dp[pos][sta] = tmp;
    return tmp;
}
int solve(int x) {
     
    int pos = 0;
    while (x) {
     
        a[pos++] = x % 10;
        x /= 10;
    }
    return dfs(pos - 1, -1, 0, true);
}
int main() {
     
    int le, ri;
    // memset(dp,-1,sizeof dp);可优化
    while (~scanf("%d%d", &le, &ri) && le + ri) {
     
        memset(dp, -1, sizeof dp);
        printf("%d\n", solve(ri) - solve(le - 1));
    }
    return 0;
}

2.F(x)（数位dp减法）

题目链接

#include 
#include 
#include 
#include 

using namespace std;
const int N = 1e4 + 5;
int dp[12][N];
int f(int x) {
     
    if (x == 0)
        return 0;
    int ans = f(x / 10);
    return ans * 2 + (x % 10);
}
int all;
int a[12];
int dfs(int pos, int sum, bool limit) {
     
    if (pos == -1) {
     
        return sum <= all;
    }
    if (sum > all)
        return 0;
    if (!limit && dp[pos][all - sum] != -1)
        return dp[pos][all - sum];
    int up = limit ? a[pos] : 9;
    int ans = 0;
    for (int i = 0; i <= up; i++) {
     
        ans += dfs(pos - 1, sum + i * (1 << pos), limit && i == a[pos]);
    }
    if (!limit)
        dp[pos][all - sum] = ans;
    return ans;
}
int solve(int x) {
     
    int pos = 0;
    while (x) {
     
        a[pos++] = x % 10;
        x /= 10;
    }
    return dfs(pos - 1, 0, true);
}
int main() {
     
    int a, ri;
    int T_T;
    int kase = 1;
    scanf("%d", &T_T);
    memset(dp, -1, sizeof dp);
    while (T_T--) {
     
        scanf("%d%d", &a, &ri);
        all = f(a);
        printf("Case #%d: %d\n", kase++, solve(ri));
    }
    return 0;
}

3.Round Numbers

题目链接
题解：题解链接

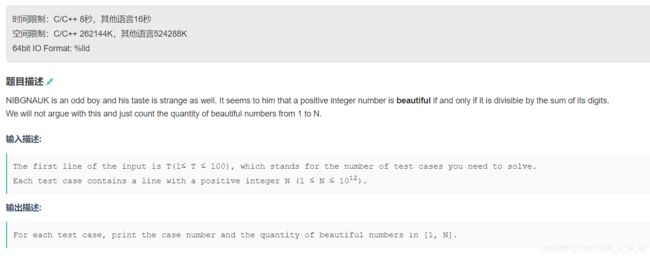
4.Beautiful Numbers

题目链接

#include 
using namespace std;
#define ll long long
int t;
int a[20];
ll dp[20][110][110][110];
ll dfs(int pos, int mod, int yu, int sum, bool limit) {
     
    if (sum > mod) {
     
        return 0;
    }
    if (pos == -1) {
     
        return mod == sum && yu == 0;
    }

    if (!limit && dp[pos][mod][yu][sum] != -1) {
     
        return dp[pos][mod][yu][sum];
    }
    int up = limit ? a[pos] : 9;
    ll ans = 0;
    for (int i = 0; i <= up; ++i) {
     
        ans +=
            dfs(pos - 1, mod, (yu * 10 + i) % mod, sum + i, limit && (i == up));
    }
    if (!limit) {
     
        dp[pos][mod][yu][sum] = ans;
    }
    return ans;
}
ll solve(ll n) {
     
    int pos = 0;
    while (n) {
     
        a[pos++] = n % 10;
        n /= 10;
    }
    ll ans = 0;
    for (int i = 1; i <= 108; ++i) {
     
        ans += dfs(pos - 1, i, 0, 0, true);
    }
    return ans;
}
int main() {
     
    cin >> t;
    memset(dp, -1, sizeof(dp));
    for (int i = 1; i <= t; ++i) {
     
        ll n;
        cin >> n;
        cout << "Case " << i << ": " << solve(n) << endl;
    }

    return 0;
}

题解：数位dp，题解链接。有一步要知道的是(yu * 10 + i) % mod，就是假如1234%3 = ((((1*10+2）%3)10+3)%310+4)%3,它们的结果是一样的