3.动规2
三角矩阵(Triangle)
问题
从顶点到最后一行的最小路径和
[
[20],
[30,40],
[60,50,70],
[40,10,80,30]
]
状态
F[0,0]到F[i,j]的最小路径和
可走路径:
F[i,j]–>F[i+1,j],F[i+1,j+1]
F[i-1, 0]–>F[i,0] (第i行第一个)
F[i-1, n-1]–>F[i, n-1] (第i行最后一个)
转移方程
F[i,j] = F[i,j] + min(F[i-1, j], F[i-1, j-1])
初始状态
F[1,0] += F[0,0]
F[1,1] += F[0,0]
返回
min(F[n-1, j])
代码
动规
class Solution {
public:
int minimumTotal(vector > &triangle) {
if (triangle.empty())return 0;
if (1 == triangle.size()) return triangle[0][0];
//F[1,0] += F[0,0]
//F[1, 1] += F[0, 0]
for (int i = 1; i < triangle.size(); ++i) {
//F[i,j] = F[i,j] + min(F[i-1, j], F[i-1, j-1])
triangle[i][0] += triangle[i-1][0];
for (int j = 1; j < triangle[i].size()-1; ++j)
triangle[i][j] += min(triangle[i-1][j], triangle[i-1][j-1]);
triangle[i][triangle[i].size() - 1] += triangle[i-1][triangle[i].size() - 2];
}
int index = triangle.size() - 1;
int res = triangle[index][0];
for (int i = 0; i < triangle[index].size(); ++i)
res = res > triangle[index][i] ? triangle[index][i] : res;
return res;
}
};
扣局部变量节省栈空间
class Solution {
public:
int minimumTotal(vector > &triangle) {
if (triangle.empty())return 0;
if (1 == triangle.size()) return triangle[0][0];
//F[1,0] += F[0,0]
//F[1, 1] += F[0, 0]
for (int i = 1; i < triangle.size(); ++i) {
//F[i,j] = F[i,j] + min(F[i-1, j], F[i-1, j-1])
triangle[i][0] += triangle[i-1][0];
for (int j = 1; j < triangle[i].size()-1; ++j)
triangle[i][j] += min(triangle[i-1][j], triangle[i-1][j-1]);
triangle[i][triangle[i].size() - 1] += triangle[i-1][triangle[i].size() - 2];
}
int res = triangle[triangle.size() - 1][0];
for (int i = 0; i < triangle[triangle.size() - 1].size(); ++i)
res = res > triangle[triangle.size() - 1][i] ? triangle[triangle.size() - 1][i] : res;
return res;
}
};

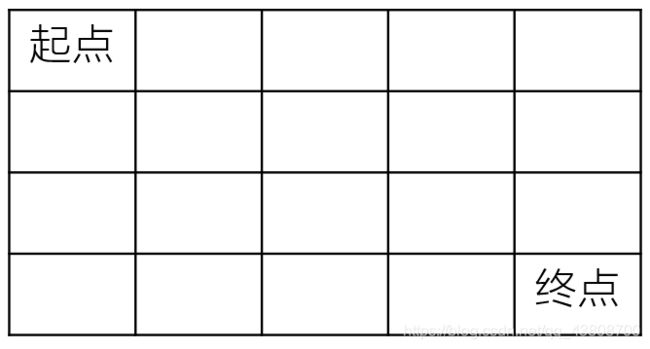
路径总数(Unique Paths)
一个机器人在m×n大小的地图的左上角(起点)。
机器人每次向下或向右移动。机器人要到达地图的右下角(终点)。
可以有多少种不同的路径从起点走到终点?
问题
从起点走到终点有多少种不同的路径
状态
F[1][1] = 0;
F[1,j] = 1
F[i,1] = 1
F[2, 2] = F[2, 1] + F[1, 2]
转移方程
F[i, j] = F[i-1, j] + F[1, j-1]
F[i, j] = 1 (1 = = i || 1 = = j)
初始状态
F[1][1] = 0;
返回
F[m, n]
代码
递归方式通不过OJ
class Solution {
public:
/**
*
* @param m int整型
* @param n int整型
* @return int整型
*/
int uniquePaths(int m, int n) {
if (1 == m && 1 == n) return 0;
if (1 == m || 1 == n) return 1;
return uniquePaths(m-1, n) + uniquePaths(m, n - 1);
}
};
动规
class Solution {
public:
/**
*
* @param m int整型
* @param n int整型
* @return int整型
*/
int uniquePaths(int m, int n) {
int** F = new int* [m + 1]();
for (int i = 0; i < m + 1; ++i)
F[i] = new int[n + 1]();
F[1][1] = 0;
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
if (1 == i || 1 == j)
F[i][j] = 1;
else
F[i][j] = F[i - 1][j] + F[i][j - 1];
}
}
return F[m][n];
}
};
扣数组行和列,减少堆区空间
class Solution {
public:
/**
*
* @param m int整型
* @param n int整型
* @return int整型
*/
int uniquePaths(int m, int n) {
int** F = new int* [m]();
for (int i = 0; i < m; ++i)
F[i] = new int[n]();
F[0][0] = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (0 == i || 0 == j)
F[i][j] = 1;
else
F[i][j] = F[i - 1][j] + F[i][j - 1];
}
}
return F[m-1][n-1];
}
};

路径总数(Unique Paths II)
继续求路径。
如果在图中加入了一些障碍,有多少不同的路径?
分别用0和1代表空区域和障碍
例如
下图表示有一个障碍在3*3的图中央。
[
[0,0,0],
[0,1,0],
[0,0,0]
]
有2条不同的路径
备注:m和n不超过100.
相较于路径总数(Unique Paths)题,无论障碍点有多少个,只需要置障碍点的数值为0就ok了
问题
考虑障碍点,从左上角到右下角可走的路径数量
状态
从F[0, 0]到F[i, j]的路径个数
转移方程
F[i, j] = 1 (0 == i || 0 == j && obstacleGrid[i, j] == 0)
F[i, j] = F[i-1, j] + F[1, j-1] (0 != i || 0 != j)
初始状态
F[0, 0] = 0
返回
F[m-1, n-1]
代码
动规,使用辅助空间vector
class Solution {
public:
/**
*
* @param obstacleGrid int整型vector>
* @return int整型
*/
int uniquePathsWithObstacles(vector >& obstacleGrid) {
if(obstacleGrid[0][0])return 0;
int row = obstacleGrid.size();
int col = obstacleGrid[0].size();
vector > pathNum(row, vector(col, 0));
for(int i=0; i 动规,使用辅助空间二维数组
class Solution {
public:
/**
*
* @param obstacleGrid int整型vector>
* @return int整型
*/
int uniquePathsWithObstacles(vector >& obstacleGrid) {
if(1 == obstacleGrid[0][0])return 0;
// write code here
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
int** F = new int* [m]();
for (int i = 0; i < m; ++i)
F[i] = new int[n]();
F[0][0] = 0;
for (int i = 0; i < m; ++i){
if(obstacleGrid[i][0]){
F[i][0] = 0;
break;
}
F[i][0] = 1;
}
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if(0 == i){
if(1 == obstacleGrid[i][j]){
F[i][j] = 0;
break;
}
F[i][j] = 1;
}
else{
if(1 == obstacleGrid[i][j]){
F[i][j] = 0;
continue;
}
F[i][j] = F[i - 1][j] + F[i][j - 1];
}
}
}
return F[m-1][n-1];
}
};
动规,不使用辅助空间
以下代码的初始状态是F[0, 0] = 1
class Solution {
public:
/**
*
* @param obstacleGrid int整型vector>
* @return int整型
*/
int uniquePathsWithObstacles(vector >& obstacleGrid) {
if(obstacleGrid[0][0])return 0;
obstacleGrid[0][0] = 1;
for(int j = 1;j=0?obstacleGrid[i][j-1]:0)+obstacleGrid[i-1][j];
}
}
return obstacleGrid[obstacleGrid.size()-1][obstacleGrid[0].size()-1];
}
};

最小路径和(Minimum Path Sum)
给定一个由非负整数填充的m x n的二维数组,现在要从二维数组的左上角走到右下角,请找出路径上的所有数字之和最小的路径。
注意:你每次只能向下或向右移动。
问题
从二维数组的左上角走到右下角数字之和的最小路径
状态
走到当前点可以从上面往下走也可以从左边往右走,因此子问题就是求从上面和左面走哪个路径和最小
F[i, j]:从F[0, 0]走到F[i, j]的最小路径
转移方程
F[i, j] = min(F[i-1, j], F[i, j-1])
F[i, j] = F[i, j-1] + a[i,j] (i==0)
F[i, j] = F[i-1, j] + a[i,j] (j==0)
初始状态
F[0,0] = a[0, 0]
返回
F[row-1][col-1]
代码
不使用辅助空间的动规
class Solution {
public:
/**
*
* @param grid int整型vector>
* @return int整型
*/
int minPathSum(vector >& grid) {
int row = grid.size();
int col = grid[0].size();
//F[i, j] = F[i, j-1] + a[i,j] (i==0)
for(int j=1; j 不使用辅助空间优化循环动规
将辅助状态F[i, j] = F[i, j-1] + a[i,j] (i==0)嵌入F[i, j] = min(F[i-1, j], F[i, j-1])的循环
class Solution {
public:
/**
*
* @param grid int整型vector>
* @return int整型
*/
int minPathSum(vector >& grid) {
int row = grid.size();
int col = grid[0].size();
//F[i, j] = F[i-1, j] + a[i,j] (j==0)
for(int i=1; i 
背包问题(也称01背包问题)
有 n 个物品和一个大小为 m 的背包. 给定数组 A 表示每个物品的大小和数组 V 表示每个物品的价值.
问最多能装入背包的总价值是多大?
1.A[i], V[i], n, m 均为整数
2.你不能将物品进行切分
3.你所挑选的要装入背包的物品的总大小不能超过 m
4.每个物品只能取一次
问题
从n个商品中选择i个商品,能够装入容量是m的包中,且商品总价值最大
如果单纯的从考虑商品单位体积的价值或者体积大小的顺序去放,会割裂商品大小和价值的关系,因此需要统一的考虑
状态
F[i, j]:从前i个商品中做选择,当包的剩余大小为m时的最大值
包的剩余空间可以放入第i个商品
A[i-1] <= j:
F[i, j] = max(F[i-1, j], F[i-1, j-A[i-1]] + V[i-1]) //主动放弃第i个包,或者预留够第i个商品的空间再从前i-1个商品中选择最大值的情况
包的剩余空间不可以放入第i个商品,被动放弃
A[i-1] > j:
F[i, j] = F[i-1, j] //从前面i-1个商品中选
F[i, j] = max(F[i-1, j], F[i-1, j-A[i-1]] + V[i-1])
包含了要放入第i个商品,需要取出部分商品和不需要取出部分商品的情况
举个例子
m=3, n=3 (m个商品,背包空间是n)
商品价值:v={3, 1, 2}
商品大小:A={2, 1, 3}
F(i, j)从前面i个商品中装空间为j的包的最大价值
A[i-1] > j:
F[i, j] = F[i-1, j]①
A[i-1] <= j:
F[i, j] = max(F[i-1, j], F[i-1, j-A[i-1]] + V[i-1]) ②
| i,j | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | 状态:F(0, 0) 最大价值:0 |
状态:F(0, 1) 最大价值:0 |
状态:F(0, 2) 最大价值:0 |
状态:F(0, 3) 最大价值:0 |
| 1 | 状态:F(1, 0) 最大价值:0 |
状态:F(1, 1) 第i个商品大小和j关系: A[i-1]:2 > j:1 转移方程:① 计算: F[1, 1] = F[0, 1] 最大价值:0 |
状态:F(1, 2) 第i个商品大小和j关系: A[i-1]:2 == j:2 转移方程:② 计算: F[1, 2] = max(F[0, 2], F[0, 0]+V[0]) 最大价值:3 |
状态:F(1, 3) 第i个商品大小和j关系: A[i-1]:2 < j:3 转移方程:② 计算: F[1, 3] = max(F[0, 3], F[0, 1]+V[0]) 最大价值:3 |
| 2 | 状态:F(2, 0) 最大价值:0 |
状态:F(2, 1) 第i个商品大小和j关系: A[i-1]:1 == j:1 转移方程:② 计算: F[2, 1] = max(F[1, 1], F[1, 0]+V[1]) 最大价值:1 |
状态:F(2, 2) 第i个商品大小和j关系: A[i-1]:1 < j:2 转移方程:② 计算: F[2, 2] = max(F[1, 2], F[1, 1]+V[1]) 最大价值:3 |
状态:F(2, 3) 第i个商品大小和j关系: A[i-1]:1 < j:3 转移方程:② 计算: F[2, 3] = max(F[1, 3], F[1, 2]+V[1]) 最大价值:4 |
| 3 | 状态:F(3, 0) 最大价值:0 |
状态:F(3, 1) 第i个商品大小和j关系: A[i-1]:3 > j:1 转移方程:① 计算: F[3, 1] = F[2, 1] 最大价值:1 |
状态:F(3, 2) 第i个商品大小和j关系: A[i-1]:3 > j:2 转移方程:① 计算: F[3, 2] = F[2, 2] 最大价值:3 |
状态:F(3, 3) 第i个商品大小和j关系: A[i-1]:3 == j:3 转移方程:② 计算: F[3, 3] = max(F[2, 3], F[2, 0]+V[2]) 最大价值:4 |
状态之间的转移关系如图所示:
转移方程
初始状态
F[0, j] = F[i, 0] = 0
返回
F[i-1, j-1]
代码
class Solution {
public:
/**
* @param m: An integer m denotes the size of a backpack
* @param A: Given n items with size A[i]
* @param V: Given n items with value V[i]
* @return: The maximum value
*/
int backPackII(int m, vector &A, vector &V) {
int n = A.size(); //商品数量
if(!n || !m)return 0;
//n+1行m+1列的二维矩阵
//F[0, j] = F[i, 0] = 0
vector > maxV(n+1, vector(m+1, 0));
for(int i=1; i<=n; ++i){
for(int j=1; j<=m; ++j){
//第i个商品小于等于当前包剩余空间
if(A[i-1] <= j){
maxV[i][j] = max(maxV[i-1][j], maxV[i-1][j-A[i-1]]+V[i-1]);
}
else
maxV[i][j] = maxV[i-1][j];
}
}
return maxV[n][m];
}
};