线性神经网络应用
3.3线性神经网络
3.3.1线性神经网络介绍
线性神经网络跟单层感知器非常类似,只是把单层感知器的sign激活函数改成了purelin函数: y=x#(3.5)
purelin函数也称为线性函数,函数图像为图3.8:
3.3.2线性神经网络分类案例
参考3.2.9中的案例,我们这次使用线性神经网络来完成相同的任务。线性神经网络的程序跟单层感知器的程序非常相似,大家可以思考一下需要修改哪些地方。
大家可以仔细阅读下面代码3-4,找到修改的部分。
代码3-4:线性神经网络案例
import numpy as np
import matplotlib . pyplot as plt
# 定义输入,我们习惯上用一行代表一个数据
X = np.array([[1,3,3],[1,4,3],[1,1,1],[1,2,1]])
# 定义标签,我们习惯上用一行表示一个数据的标签
T =np.array([[1],[1],[-1],[-1]])
# 权值初始化,3行1列
# np.random.random可以生成0-1的随机数
W = np.random.random([3,1])
# 学习率设置
lr = 0.1
# 神经网络输出
Y = 0
# 更新一次权值
def train():
# 使用全局变量X,Y,W,lr
global X,Y,W,lr
# 同时计算4个数据的预测值
# Y的形状为(4,1)-4行1列
Y = np.dot(X,W)
# T - Y得到4个的标签值与预测值的误差E。形状为(4,1)
E =T - Y
# X.T表示X的装置矩阵,形状为(3,4)
# 我们一共有4个数据,每个数据3个值。定义第i个数据的第j个特征值为xij
# 如第1个数据,第2个值为x12
# X.T.dot(T - Y)为一个3行1列的数据:
# 第1行等于:x00×e0+x10×e1+x20×e2+x30×e3,它会调整第1个神经元对应的权值
# 第2行等于:x01×e0+x11×e1+x21×e2+x31×e3,它会调整第2个神经元对应的权值
# 第3行等于:x02×e0+x12×e1+x22×e2+x32×e3,它会影调整3个神经元对应的权值
# X.shape表示X的形状X.shape[0]得到X的行数,表示有多少个数据
# X.shape[1]得到列数,表示每个数据有多少个特征值。
delta_W =lr (X.T.dot(E)) / X.shape[0]
W =W + delta_W
# 训练100次
for i in range(100):
# 更新一次权值
train()
#————————以下为画图部分————————#
# 正样本的xy坐标
x1 = [3,4]
y1 = [3,3]
# 负样本的xy坐标
x2 = [1,2]
y2 = [1,1]
# 计算分界线的斜率以及截距
# 因为正负样本的分界是0,所以分界线的表达式可以写成:
# w0 × x0 + w1 × x1 + w2 × x2 = 0
# 其中x0为1,我们可以把x1,x2分别看成是平面坐标系中的x和y
# 可以得到:w0 + w1×x + w2 × y = 0
# 从而推导出:y = -w0/w2 - w1×x/w2,因此可以得到
k = - W[1] / W[2]
d = - W[0] / W[2]
# 设定两个点
xdata = (0,5)
# 通过两个点来确定一条直线,用红色的线来画出分界线
plt.plot(xdata,xdata k + d,'r')
# 用蓝色的点画出正样本
plt.scatter(x1,y1,c='b')
# 用黄色的点来画出负样本
plt.scatter(x2,y2,c='y')
# 显示图案
plt.show()
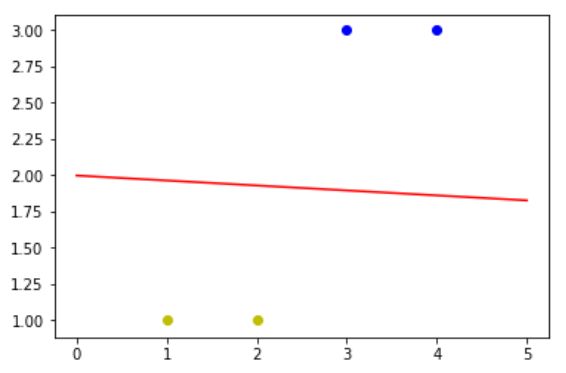
程序的输出结果为:
线性神经网络的程序有两处是对单层感知器程序进行了修改。
第一处是在train()函数中,将Y = np.sign(np.dot(X,W))改成了Y = np.dot(X,W)。因为线性神经网络的激活函数是y=x,所以这里就不需要np.sign()了。
第二处是在for i in range(100)中,把原来的:
# 训练100次
for i in range(100):
# 更新一次权值
train()
# 打印当前训练次数
print ('epoch:',i + 1)
# 打印当前权值
print ('weights:',W)
# 计算当前输出
Y = np.sign(np.dot(X,W))
# .all()表示Y中的所有值跟T中所有值都对应相等,结果才为真
if (Y == T).all():
print ('Finished')
# 跳出循环
break
改成了:
# 训练100次
for i in range(100):
# 更新一次权值
train()
在单层感知器中,当y等于t时,Δw=0就会为0,模型训练就结束了,所以可以提前跳出循环。单层感知器使用的模型收敛条件是两次迭代模型的权值已经不再发生变化,则可以认为模型收敛。
而在线性神经网络中,y会一直逼近t的值,不过一般不会得到等于t的值,所以可以对模型不断进行优化。线性神经网络使用的模型收敛条件是设置一个最大迭代次数,当训练了一定次数后就可以认为模型收敛了。
对比单层感知器和线性神经网络所得到的结果,我们可以看得出线性神经网络所得到的结果会比单层感知器得到的结果更理想。但是线性神经网络也还不够优秀,当使用它处理非线性问题的时候,它就不能很好完成工作了。
3.3.3线性神经网络处理异或问题
首先我们先来回顾一下异或运算。
0与0异或等于0
0与1异或等于1
1与0异或等于1
1与1异或等于0
代码3-5:线性神经网络-异或问题
# 输入数据
# 4个数据分别对应0与0异或,0与1异或,1与0异或,1与1异或
X = np.array([[1,0,0],[1,0,1],[1,1,0], [1,1,1]])
# 标签,分别对应4种异或情况的结果
# 注意这里我们使用-1作为负标签
T = np.array([[-1],[1],[1],[-1]])
# 权值初始化,3行1列
# np.random.random可以生成0-1的随机数
W = np.random.random([3,1])
# 学习率设置
lr = 0.1
# 神经网络输出
Y = 0
# 更新一次权值
def train():
# 使用全局变量X,Y,W,lr
global X,Y,W,lr
# 计算网络预测值
Y = np.dot(X,W)
# 计算权值的改变
delta_W =lr (X.T.dot(T - Y)) / X.shape[0]
# 更新权值
W =W + delta_W
# 训练100次
for i in range(100):
#更新一次权值
train()
#————————以下为画图部分————————#
# 正样本
x1 = [0,1]
y1 = [1,0]
# 负样本
x2 =[0,1]
y2 = [0,1]
# 计算分界线的斜率以及截距
k = - W[1] / W[2]
d = - W[0] / W[2]
# 设定两个点
xdata = (-2,3)
# 通过两个点来确定一条直线,用红色的线来画出分界线
plt.plot(xdata,xdata k + d,'r')
# 用蓝色的点画出正样本
plt.scatter(x1,y1,c='b')
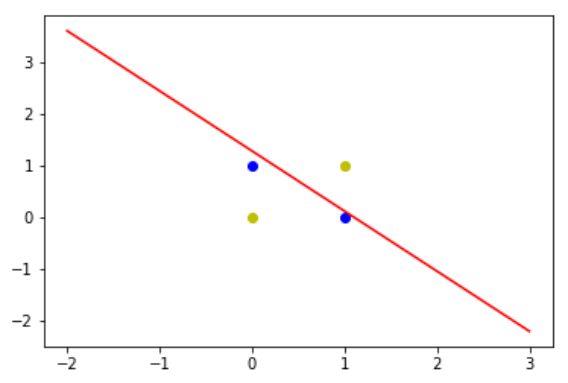
程序的输出结果为:
从结果我们能够看出用一条直线并不能把异或问题中的两个类别给划分开来,因为这是一个非线性的问题,可以使用非线性的方式来进行求解。
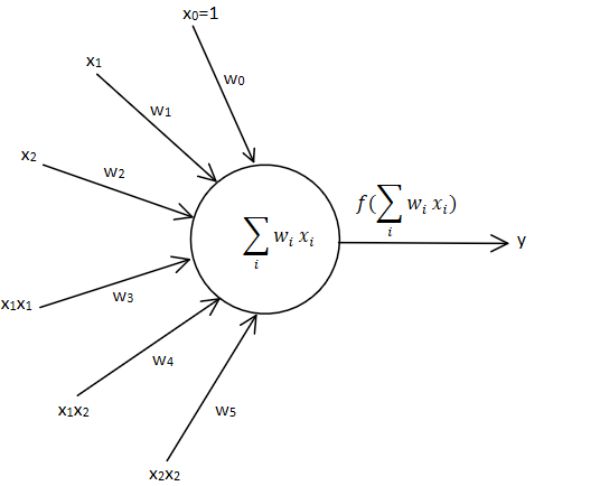
其中一种方式是我们可以给神经网络加入非线性的输入。代码3-5中的输入信号只有3个信号x0,x1,x2,我们可以利用这3个信号得到带有非线性特征的输入:x0,x1,x2,x1×x1,x1×x2,x2×x2,其中x1×x1,x1×x2,x2×x2为非线性特征。神经网络结构图如图3.9所示:
代码3-6:线性神经网络引入非线性特征解决异或问题
import numpy as np
import matplotlib.pyplot as plt
# 输入数据
# 原来X的3个特征分别为:x0,x1,x2
# X = np.array([[1,0,0],
# [1,0,1],
# [1,1,0],
# [1,1,1]])
# 给网络输入非线性特征
# 现在X的6个特征分别为:x0,x1,x2,x1×x1,x1×x2,x2×x2
X = np.array([[1,0,0,0,0,0],[1,0,1,0,0,1],[1,1,0,1,0,0],[1,1,1,1,1,1]])
# 标签,分别对应4种异或情况的结果
T = np.array([[-1],[1],[1],[-1]])
# 权值初始化,6行1列
# np.random.random可以生成0-1的随机数
W = np.random.random([6,1])
# 学习率设置
lr = 0.1
# 神经网络输出
Y = 0
# 更新一次权值
def train():
# 使用全局变量X,Y,W,lr
global X,Y,W,lr
# 计算网络预测值
Y = np.dot(X,W)
# 计算权值的改变
delta_W =lr (X.T.dot(T - Y)) / X.shape[0]
# 更新权值
W =W + delta_W
# 训练1000次
for i in range(1000):
#更新一次权值
train()
# 计算模型预测结果并打印
Y = np.dot(X,W)
print(Y)
#————————以下为画图部分————————#
# 正样本
x1 = [0,1]
y1 = [1,0]
# 负样本
x2 = [0,1]
y2 = [0,1]
# 因为正负样本的分界是0,所以分界线的表达式可以写成:
# w0x0 + w1x1 + w2x2 + w3x1x1 + w4x1x2 + w5x2x2 = 0
# 其中x0为1,我们可以把x1,x2分别看成是平面坐标系中的x和y
# 可以得到:w0 + w1x + w2y + w3xx + w4xy + w5yy = 0
# 整理可得:w5y² + (w2+w4x)y + w0 + w1x + w3x² = 0
# 其中 a = w5, b = w2+w4x, c = w0 + w1x + w3x²
# 根据一元二次方程的求根公式:ay²+by+c=0,y=[-b±(b^2-4ac)^(1/2)]/2a
def calculate(x,root):
# 定义参数
a = W[5]
b = W[2] +x W[4]
c = W[0] +x W[1] +x x W[3]
# 有两个根
if root == 1:
return (-b + np.sqrt(b b - 4 a c)) / (2 a)
if root == 2:
return (-b - np.sqrt(b b - 4 a c)) / (2 a)
# 从-1到2之间均匀生成100个点
xdata = np.linspace(-1,2,100)
# 使用第一个求根公式计算出来的结果画出第一条红线
plt.plot(xdata,calculate(xdata,1),'r')
# 使用第二个求根公式计算出来的结果画出第二条红线
plt.plot(xdata,calculate(xdata,2),'r')
# 蓝色点表示正样本
plt.plot(x1,y1,'bo')
# 黄色点表示负样本
plt.plot(x2,y2,'yo')
# 绘图
plt.show()
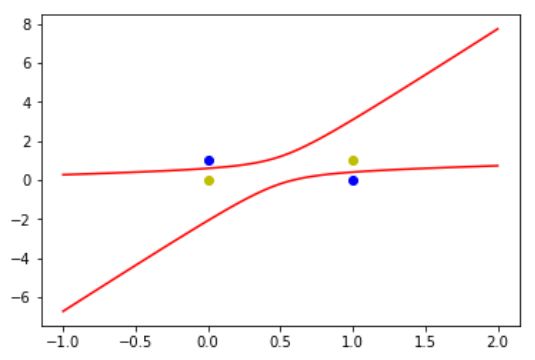
程序的输出结果为:
[[-0.98650596]
[ 0.990989 ]
[ 0.990989 ]
[-0.99302749]]
从输出的预测值我们可以看出,预测值与真实标签的数值是非常接近的,几乎相等,说明预测值很符合我们想要的结果。而从输出图片中也能观察到两条曲线的内部是负样本所属的类别,两条曲线的外部是正样本所属的类别。这两条曲线很好地把两个类别区分开了。
线性神经网络可以通过引入非线性的输入特征来解决非线性问题,但这并不是一种非常好的解决方案。下一章节我们将介绍一种新的神经网络,BP(Back Propagation)神经网络,通过学习BP神经网络我们可以获得更好的解决问题的思路。