具有领域半径自适应初始化函数松鼠算法用于解决TSP问题
具有领域半径自适应初始化函数松鼠算法用于解决tsp问题
问题描述
Tsp问题,即旅行商问题,又译为旅行推销员问题,货郎担问题,是数学领域中著名问题之一,假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
TSP问题是一个组合优化问题。该问题可以被证明具有NPC计算复杂性。因此,任何能使该问题的求解得以简化的方法,都将受到高度的评价和关注。
旅行推销员问题是图论中最著名的问题之一,即“已给一个n个点的完全图,每条边都有一个长度,求总长度最短的经过每个顶点正好一次的封闭回路”。Edmonds,Cook和Karp等人发现,这批难题有一个值得注意的性质,对其中一个问题存在有效算法时,每个问题都会有有效算法。
迄今为止,这类问题中没有一个找到有效算法。倾向于接受NP完全问题(NP-Complete或NPC)和NP难题(NP-Hard或NPH)不存在有效算法这一猜想,认为这类问题的大型实例不能用精确算法求解,必须寻求这类问题的有效的近似算法。
我们在这一大类问题之下选择了tsplib当中的att48问题,att48问题含有48个城市,且属于对称图,在距离的计算当中采取伪欧氏距离。
算法描述
松鼠算法(SSA),是受到自然界中一种飞行松鼠的启发,所提出的一种新颖的全局优化算法,松鼠觅食算法。它主要通过模仿一种飞行松鼠的觅食行为和他们被称为滑翔的运动方式。该算法主要分为下列步骤:
- 具有邻域搜索功能初始化
首先随机选取起点城市,之后利用邻域半径自适应函数计算当前城市的邻域半径,在计算出领域半径之后,确定邻域内的城市,并应用三角概率分布赋予邻域内每个城市概率,在此概率区间内随机产生一个数字,依该数字所在城市概率区间选取下一个城市。计算未到城市数目,若大于1则继续上面操作,若等于1则直接将最后一个城市作为下一站城市,输出遍历所有城市的路线。(相较于传统的随机初始化,这样进行初始化,会大大的降低算法的运行时间,因为初始点相对于随机初始化,这样的初始点明显更加优秀)。
重复生成直到生成足够多个个体,然后对每个个体的fitness进行计算。 - 松鼠排序
根据计算后的fitness值进行排序,并将fitness最佳的个体定为最优个体,2-4个个体定为次优个体。 - 松鼠觅食跳跃
松鼠开始进行跳跃觅食操作,主要体现为最优个体路径链不会发生任何改变,次优个体的路径链会向最优解靠拢(此处的靠拢类似于遗传算法当中的交叉操作,但是最优个体是不发生改变的),普通个体且未被标记过的会向次优解靠拢,并且在靠拢过后被标记为已向次优解靠拢过个体,普通个体且被标记过的会向最优解靠拢。 - 季节变化
类似于遗传算法的变异操作,单纯的跳跃操作将会导致算法相对容易陷入局部最优解,从而降低算法效率,因此在这里会进行跳出局部最优解,随机靠拢的操作。
算法的具体实现
1.具有邻域搜索功能初始化
Random random=new Random();
TSP p1=(TSP) p;
double[][] distance=p1.distance;
while (!(solutionS.array.size()==population)) {
int first = random.nextInt(65535) % cityNum;//随机生成第一个点
SSATspSolution sds = new SSATspSolution();
sds.city_cycle.add(first);
while (sds.city_cycle.size() < cityNum - 1) {
initR(first,cityNum,distance,sds.city_cycle);
initD(p1);
double r=(
(rmax-rmin)/ (1+
Math.exp((ravg-dmin)/(davg-dmin)
)
)
)+rmin;
ArrayList<Integer> citys=new ArrayList<>();
citys=getcitys(r,distance,cityNum,first,sds.city_cycle);
int next=get_next(first,citys,distance);
//System.out.println(next);
sds.city_cycle.add(next);
first=next;
}
for (int i=0;i<cityNum;i++){
if (!sds.city_cycle.contains(i)){
sds.city_cycle.add(i);
//System.out.println(sds.city_cycle.size());
break;
}
}
sds=p1.evalute(sds);
solutionS.array.add(sds);
}
return solutionS;
该部分的思路属于一个独特的启发式算法初始化思路,我们将这一部分的伪代码单独列在下面
FTPCANA算法流程如下:
步骤 1 对所有城市进行编码。
步骤 2 随机选取起点城市。
步骤 3 利用邻域半径自适应函数计算当前城市的
邻域半径。
步骤 4 确定邻域内的城市,并应用三角概率分布赋
予邻域内每个城市概率。
步骤 5 在概率区间内随机产生一个数字,依该数字
所在城市概率区间选取下一个城市。
步骤 6 计算未到城市数目,若大于 1则步骤 3,若等
于 1则步骤 7。
步骤 7 直接将最后一个城市作为下一站城市。
步骤 8 输出遍历所有城市的路线。
相关函数计算方法如下
dmin=Double.MAX_VALUE;
double sum=0;
davg=0;
for (int i=0;i<t.cityNum;i++){
for (int j=0;j<t.cityNum;j++){
sum+=t.distance[i][j];
if (t.distance[i][j]<dmin){
dmin=t.distance[i][j];
}
}
}
davg=sum/t.cityNum;
rmin=Double.MAX_VALUE;
rmax=Double.MIN_VALUE;
double sum=0;
int h=0;
ravg=0;
for (int i=0;i<cityNum;i++){
if (!city_cycle.contains(i)){
//这里的city_cycle相当于是一个禁忌表
sum+=distance[a][i];
h++;
if (distance[a][i]>rmax){
rmax=distance[a][i];
}
if (distance[a][i]<rmin){
rmin=distance[a][i];
}
}
}
ravg=sum/h;
2.松鼠排序
for (int i=0;i<s.array.size();i++){
for (int j=0;j<s.array.size()-1-i;j++){
//冒泡排序
if (s.array.get(j).fitness>s.array.get(j+1).fitness){
SSATspSolution a= SSATspSolution.clone(s.array.get(j));
SSATspSolution b=SSATspSolution.clone(s.array.get(j+1));
s.array.set(j,b);
s.array.set(j+1,a);
}
}
}
//冒泡排序结束,开始声明程序
for (int i=0;i<is_best;i++)
s.array.get(i).is_best=true;
//标记到达过最优解的松鼠
for (int i=is_best;i<is_best+is_sec_best;i++)
s.array.get(i).is_sec_best=true;
//标记到达过次优解的松鼠
return s;
3.松鼠觅食跳跃
for (int i = SSA.is_best; i<s.array.size(); i++){
double dg=0.5+Math.random()*0.61;
double r=Math.random();//是否遇到捕食者的标尺
double pdp=0.1;//不遇到捕食者的最低限度
if (r>=pdp)//产生新位置,没有遇到捕食者,如果存在捕食者就原地不动
{
if (i>=SSA.is_best&&i<(SSA.is_best+SSA.is_sec_best)){
//======>>对于次优解来说。<<========
for (int j=0;j<s.array.get(0).city_cycle.size();j++){
//针对于每一个维度
int a, b, c, flag;
int ran1, ran2, temp;
int[] Gh1 = new int[cityNum];
ran1 = random.nextInt(65535) % cityNum;
ran2 = random.nextInt(65535) % cityNum;
while (ran1 == ran2) {
//如果交叉位置相同的话
ran2 = random.nextInt(65535) % cityNum;
}
if (ran1 > ran2)// 确保ran1
{
temp = ran1;
ran1 = ran2;
ran2 = temp;
}
flag = ran2 - ran1 + 1;// 删除重复基因前染色体长度
for (a = 0, b = ran1; a < flag; a++, b++) {
Gh1[a] = s.array.get(0).city_cycle.get(b);//交叉基因组1
}
// 已近赋值i=ran2-ran1个基因
for (c = 0, b = flag; b < cityNum;)// 染色体长度
{
Gh1[b] = s.
array.get(i).
city_cycle.get(c++);//对个体1的基因组进行读取
for (a = 0; a < flag; a++) {
if (Gh1[a] == Gh1[b]) {
break;
}
}
if (a == flag) {
b++;
}
}
for (a = 0; a < cityNum; a++) {
s.array.get(i).city_cycle.set(a, Gh1[a]);// 交叉完毕放回种群
}
}
}
else if (i>=SSA.is_best+SSA.is_sec_best&&s.array.get(i).is_sec_best==false){
//对于普通解,但曾经wei去过ci优解的个体来说
int which_second_best = (int) (SSA.is_best + Math.random() * (SSA.is_sec_best));
for (int j = 0; j < s.array.get(0).city_cycle.size(); j++) {
//针对于每一个维度
int a, b, c, flag;
int ran1, ran2, temp;
int[] Gh1 = new int[cityNum];
ran1 = random.nextInt(65535) % cityNum;
ran2 = random.nextInt(65535) % cityNum;
while (ran1 == ran2) {
//如果交叉位置相同的话
ran2 = random.nextInt(65535) % cityNum;
}
if (ran1 > ran2)// 确保ran1
{
temp = ran1;
ran1 = ran2;
ran2 = temp;
}
flag = ran2 - ran1 + 1;// 删除重复基因前染色体长度
for (a = 0, b = ran1; a < flag; a++, b++) {
Gh1[a] = s.array.get(which_second_best).city_cycle.get(b);//交叉基因组1
}
// 已近赋值i=ran2-ran1个基因
for (c = 0, b = flag; b < cityNum;)// 染色体长度
{
Gh1[b] = s.array.
get(i).
city_cycle.
get(c++);//对个体1的基因组进行读取
for (a = 0; a < flag; a++) {
if (Gh1[a] == Gh1[b]) {
break;
}
}
if (a == flag) {
b++;
}
}
for (a = 0; a < cityNum; a++) {
s.array.get(i).city_cycle.set(a, Gh1[a]);// 交叉完毕放回种群
}
}
}else if (i>=SSA.is_best+SSA.is_sec_best&&s.array.get(i).is_sec_best==true){
//对于普通解但是去过次优解的解来说
for (int j=0;j<s.array.get(0).city_cycle.size();j++){
//针对于每一个维度
int a, b, c, flag;
int ran1, ran2, temp;
int[] Gh1 = new int[cityNum];
ran1 = random.nextInt(65535) % cityNum;
ran2 = random.nextInt(65535) % cityNum;
while (ran1 == ran2) {
//如果交叉位置相同的话
ran2 = random.nextInt(65535) % cityNum;
}
if (ran1 > ran2)// 确保ran1
{
temp = ran1;
ran1 = ran2;
ran2 = temp;
}
flag = ran2 - ran1 + 1;// 删除重复基因前染色体长度
for (a = 0, b = ran1; a < flag; a++, b++) {
Gh1[a] = s.array.get(0).city_cycle.get(b);//交叉基因组1
}
// 已近赋值i=ran2-ran1个基因
for (c = 0, b = flag; b < cityNum;)// 染色体长度
{
Gh1[b] = s.array.get(i).city_cycle.get(c++);//对个体1的基因组进行读取
for (a = 0; a < flag; a++) {
if (Gh1[a] == Gh1[b]) {
break;
}
}
if (a == flag) {
b++;
}
}
for (a = 0; a < cityNum; a++) {
s.array.get(i).city_cycle.set(a, Gh1[a]);// 交叉完毕放回种群
}
}
}
}else{
s.array.get(i).city_cycle.set(0,random.nextInt(65535) % cityNum);//这里就是想初始化一条路径而已,
// 我也不知道那个看起来很玄学的65535是干嘛的
for (int m = 1; m < cityNum;)// 染色体长度
{
s.array.get(i).city_cycle.set(m,random.nextInt(65535) % cityNum);
int j;
for (j = 0; j < m; j++) {
if (s.array.get(i).city_cycle.get(m) == s.array.get(i).city_cycle.get(j)) {
//如果相同,那就得重新来,路径不能重复
break;
}
}
if (j == m) {
m++;
}
}
}
}
return s;
在这一部分的操作当中,我们将跳跃松鼠的染色体对目标松鼠染色体的部分进行学习,并且产生新的跳跃松鼠染色体,首先通过随机数截取目标松鼠的染色体片段作为新松鼠染色体片段的开始,之后对之前的跳跃松鼠进行遍历,将新松鼠染色体片段中不存在的染色体进行补充,直到生成一条新的路径链。与这种交换方式相对应,还存在一种更加类似于现实中染色体进行交换的操作方式
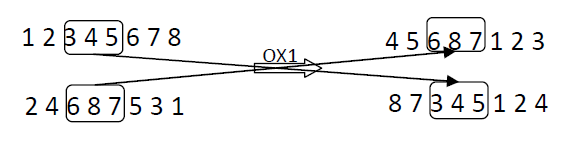
类似与这种,但是需要注意的是,在松鼠算法之中,目标松鼠的染色体是不会发生变化的,发生变化的只有跳跃松鼠,而且同时使用这种跳跃方式,需要注意,城市路径链是否完整或者是存在重复的城市。
4.季节变化
double Sct = s.array.get(0).fitness-best;
if (Sct<0){
Sct=0-Sct;
}
double Smin = 1 / Math.pow(365, 2.5 * t / generation);
double mc=Math.random();
if (Sct <= Smin) {
//变异操作\
System.out.println("bianyi");
for (int i=2;i<s.array.size();i++){
int ran1, ran2, temp,count;
Random random=new Random();
ran1 = random.nextInt(65535) % cityNum;
ran2 = random.nextInt(65535) % cityNum;
while (ran1 == ran2) {
ran2 = random.nextInt(65535) % cityNum;
}
temp = s.array.get(i).city_cycle.get(ran1);
s.array.get(i).city_cycle.set(ran1,s.array.get(i).city_cycle.get(ran2));
s.array.get(i).city_cycle.set(ran2,temp);
}
}
return s;
best是指上一代中的最佳,sct的含义是指这一代最佳与上一代最佳的差值,如果差值过于接近,以至于趋近于季节值,那我们认为进入冬季,松鼠开始进行随机跳跃。
结果展示
由于时间复杂性不同,GA算法控制在100000代循环,SSA算法控制在10000代循环,两者的时间均在可接受的范围内。
att48 理想情况:10628
GA算法:
11398
11653
11451
11149
11364
SSA算法:
11161
11230
11133
10965
11088
经过上述结果,我们可以清楚地看到相较于GA算法,SSA算法虽然代数较小,但仍然表现出了比GA算法更为优越的效果,同样的GA算法虽然准确性相对于SSA算法来说有所不如,但是从时间复杂度来说,算法实现更为简单的GA算法明显有着更为优秀的表现