基于能量均衡高效WSN的LEACH协议改进算法
文章目录
- 一、理论基础
-
- 1、间距因子
- 2、剩余能量因子
- 3、密度因子
- 4、权值的选取
- 二、算法流程
- 三、仿真实验及性能分析
-
- 1、仿真参数设置
- 2、实验结果及分析
- 四、参考文献
- 五、Matlab代码
一、理论基础
由于LEACH协议的随机选择簇首原则,可能导致地理条件不佳和能量剩余不足的节点被选为簇首节点。因此本文加入3个因子:间距因子、剩余能量因子和密度因子。综合权衡这几方面,对LEACH协议的 T ( n ) T(n) T(n)计算式进行改进,减少条件不足的节点当选为簇首的概率,减缓节点的枯竭速度,均衡整个网络的能量负载,避免部分节点提前枯竭死亡导致的网络瘫痪。
1、间距因子
无线传输的发射功率和接收功率之间的关系可以表示为 P R = P T r n (1) PR=\frac{PT}{r}n\tag{1} PR=rPTn(1)其中, P R PR PR是无线传输的接收功率, P T PT PT是无线传输的发射功率, r r r是传输距离, n n n定义为传播因子,其大小由无线传播的即时环境所决定。由式(1)可以得出,接收信号强弱和信号传输距离的成反比关系。因此,普通节点间距sink距离越远收到的信号越弱,反之,则越强。利用以上原理,可以得出节点之间大概距离。首先,sink节点在网络监测区域内广播一个信号。然后,各个节点通过接收信号的强弱,得到本身与sink节点的大概间距,并将自己的id和剩余能量信息反馈给sink节点。
间距因子定义如下 w = d i − d m i n d m a x − d m i n (2) w=\frac{d_i-d_{min}}{d_{max}-d_{min}}\tag{2} w=dmax−dmindi−dmin(2)其中, d m a x d_{max} dmax和 d m i n d_{min} dmin分别代表网络中节点到sink间距的最远和最近值。通常情况下, d m a x d_{max} dmax取监测区域最远两点的距离。
2、剩余能量因子
定义各个节点的剩余能量因子为 E r e = E c E m (3) E_{re}=\frac{E_c}{E_m}\tag{3} Ere=EmEc(3)其中, E c E_c Ec为节点当前剩余能量,而 E m E_m Em为节点的最初能量,引入节点的剩余能量因子要充分考虑节点的剩余能量,使簇首的选取更为合理。
3、密度因子
节点的密度因子衡量的是节点附近的其他节点的数量多少。因为在 WSN 实际监测场景中,节点都是随机散布在监测区域,每个节点的附近节点数量不同。因此在簇首选取时,也要考虑该节点附近的数量多少。若附近节点数量很少甚至没有,该节点不适合为簇首。在这里所谓的附近节点,只有在该节点的最大可覆盖通信范围 R R R内的其他节点,才能称为该节点的附近节点。即邻居节点的集合为 N n b = { j ∣ d ( i , j ) ≤ R , j ∈ N } , i ∈ { 1 , 2 , ⋯ , N } (4) N_{nb}=\{j|d(i,j)≤R,j∈N\},i∈\{1,2,\cdots,N\}\tag{4} Nnb={ j∣d(i,j)≤R,j∈N},i∈{ 1,2,⋯,N}(4)节点的密度因子是在节点的最大可覆盖通信范围 R R R内,节点的附近节点数量与标准的簇中节点数量的比。节点的最大可覆盖通信范围 R R R计算公式和节点 n n n的相对密度计算公式分别为 R = S π N p (5) R=\sqrt{\frac{S}{\pi Np}}\tag{5} R=πNpS(5) ρ = i . N n b ( 1 p − 1 ) (6) \rho=\frac{i.N_{nb}}{\left(\frac1p-1\right)}\tag{6} ρ=(p1−1)i.Nnb(6)其中,定义 ρ \rho ρ为密度因子, i . N n b i.N_{nb} i.Nnb为节点 i i i在其标准通信半径内的邻居节点的数量, S S S为监测范围面积大小。 N N N为监测范围内节点的数量, p p p表示簇首的数量占所有节点数量的百分比, ( 1 p − 1 ) (\frac1p-1) (p1−1)为标准簇中附近节点的数量。因此,充分考虑了候选簇首的剩余能量因子、间距因子和附近的节点数目,更新阈值公式为 T ( n ) = { p 1 − p ( r m o d ( 1 p ) ) ( λ 1 E r e + λ 2 ( 1 − w ) + λ 3 ρ ) , n ∈ G 0 , n ∉ G (7) T(n)=\begin{dcases}\frac{p}{1-p\left(rmod(\frac1p)\right)}(\lambda_1E_{re}+\lambda_2(1-w)+\lambda_3\rho),n∈G\\0,\quad\quad\quad\quad n∉G\end{dcases}\tag{7} T(n)=⎩⎪⎨⎪⎧1−p(rmod(p1))p(λ1Ere+λ2(1−w)+λ3ρ),n∈G0,n∈/G(7)
4、权值的选取
通过Matlab软件进行仿真实验,经过多次实验验证,在此实验场景中将密度因子的加权值 λ 3 \lambda_3 λ3设成0.2仿真效果较好。对于节点的剩余能量因子的加权值 λ 1 \lambda_1 λ1,随着轮次的增加,剩余能量的越来越少,为了减少节点的死亡速度,均衡各个节点的能量,需要更加侧重考虑剩余能量的因素。因此,随着网络传输的进行可以逐步增加剩余能量因子的加权值。本文设计在节点数据传输初期,各个节点的能量都较大,此时剩余能量因子的加权因子取较小值 λ 1 = 0.2 \lambda_1=0.2 λ1=0.2,增大间距因子的加权值;当节点的能量少于50%时,剩余能量的加权因子取较大值 λ 1 = 0.6 \lambda_1=0.6 λ1=0.6,间距因子的加权值就要相对减少。因为节点一旦被分布好,通常不再移动。因此,理论上说,节点的间距因子的加权值不用改变。但是,由于前2个因素的权重的变化,间距因子的加权值也会相应改变。因为各个因子的加权值总满足和为1。
二、算法流程
三、仿真实验及性能分析
1、仿真参数设置
用Matlab软件仿真进行实验,通过进行2000轮的实验,从存活节点数量和能量消耗两方面,将LEACH-improved路由协议、经典的LEACH协议和LEACH-E协议的实验结果进行对比。假设在100×100m的规则监测范围内不均匀地分散了100个节点,其中,sink节点坐标位于(50,50)。其他仿真参数设置为: E 0 = 0.5 J , E e l e c = 50 n J / b i t , E d a = 5 n J / b i t , ε f s = 10 p J / b i t / m 2 , ε m p = 0.0013 p J / b i t / m 2 E_0=0.5J,E_{elec}=50nJ/bit,E_{da}=5nJ/bit,\varepsilon_{fs}=10pJ/bit/m^2,\varepsilon_{mp}=0.0013pJ/bit/m^2 E0=0.5J,Eelec=50nJ/bit,Eda=5nJ/bit,εfs=10pJ/bit/m2,εmp=0.0013pJ/bit/m2,数据分组的大小为4000bit。
2、实验结果及分析
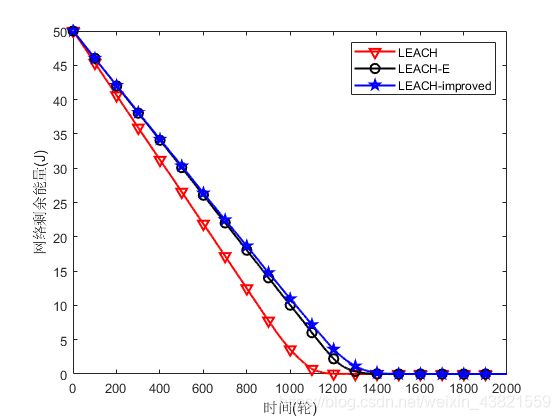
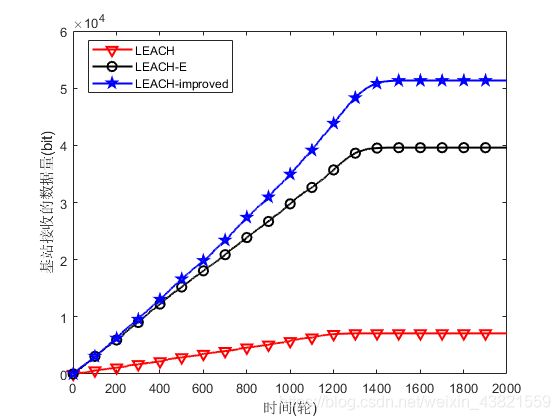
图2、图3和图4显示了,随着仿真时间的增加,仿真实验分别采用LEACH协议、LEACH-E协议与LEACH-improved协议,在3种不同情况下的网络中节点存活数量变化情况、网络剩余能量和基站接收的数据量方面的仿真结果比较。

由此可知,新的路由协议使簇首选举更加合理,簇首分布更加均匀,均衡了簇间能耗,减少了网络能量消耗,延长网络生命周期。
四、参考文献
[1] 黄利晓, 王晖, 袁利永,等. 基于能量均衡高效WSN的LEACH协议改进算法[J]. 通信学报, 2017, v.38;No.365(S2):164-169.
[2] Heinzelman W R , Chandrakasan A , Balakrishnan H . Energyefficient communication protocol for wireless microsensor networks. 2000.
[3] 韩广辉,张丽翠.基于LEACH协议的无线传感网能效分簇算法[J].吉林大学学报(信息科学版),2017,35(01):26-31.
五、Matlab代码
下载地址:
https://download.csdn.net/download/weixin_43821559/17141009