数据结构复习笔记————堆
堆
- 1.堆的概念和性质
-
- (1)概念
- (2)性质:
- 2.堆的实现
-
- (1)堆的向下调整方法
- (2)利用堆将数组排一个升序
- 3.堆接口的具体实现
-
- (1)创建堆结构体
- (2) 堆的初始化
- (3)插入数据
- (4)向上调整函数
- (5)删除一个数据
- (6)求堆中有多少个数
- (7)返回堆顶的第一个数
- 完!

1.堆的概念和性质
(1)概念
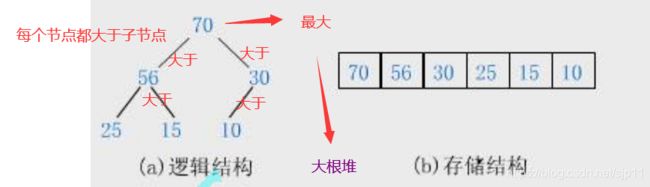
堆是一颗特殊的完全二叉树,只是它这个树所有的节点不大于父亲节点或者所有的节点不小于父亲节点,则称为大堆或小堆
根节点最大的叫大根堆,根节点最小的叫小根堆
(2)性质:
堆中每个节点总是不大于子节点或不小于子节点
堆总是一颗完全二叉树
逻辑结果是我们想象出来的,为了方便于我们理解,而实际中堆的存储结构式以数组的形式存储

选择题:
1.下列关键字序列为堆的是:()
A 100,60,70,50,32,65
B 60,70,65,50,32,100
C 65,100,70,32,50,60
D 70,65,100,32,50,60
E 32,50,100,70,65,60
F 50,100,70,65,60,32
2.堆的实现
(1)堆的向下调整方法
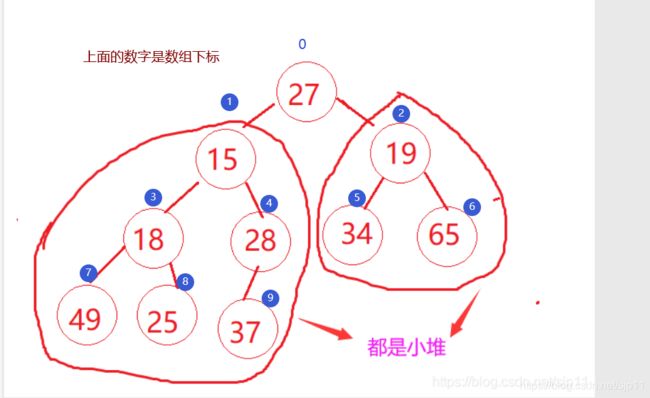
现在我们给出一个数组,逻辑上看做一颗完全二叉树。我们通过从根节点开始的向下调整算法可以把它调整
成一个小堆。向下调整算法有一个前提:左右子树必须是一个堆,才能调整。
int a[] = {27,15,19,18,28,34,65,49,25,37};
向下调整算法的前提是:左右子树必须是一个堆,如果根节点的的左右子树都不是堆怎么办?别急,这些在后面都会讲到
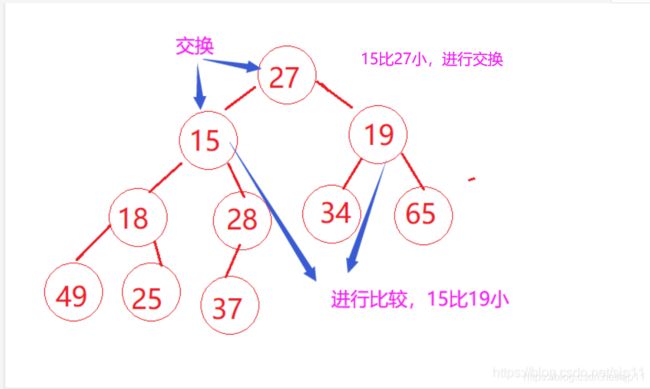
1.找出左右孩子中较小那个值
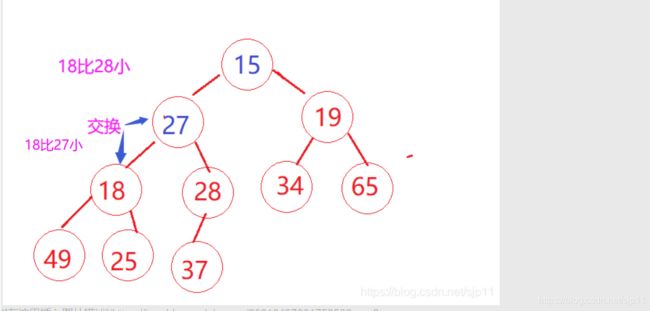
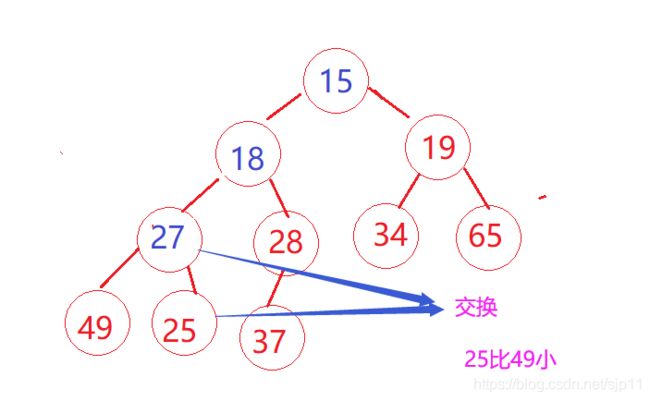
2.如果小的孩子节点比父亲节点要小,则跟父亲节点交换,并且把原来的孩子位置当成父亲,继续向下调整,直到走到叶子节点。
如果小的孩子比父亲大,则不需要调整,此时的堆已经是小堆
假设父亲的下标为parent,则它的左孩子的下标一定为leftchild=2×parent+1,右孩子rightchild=2×parent+2
该算法的时间复杂度为O(logn)
我们给出任意一个数组,如果左右子树都不是小堆怎么办?
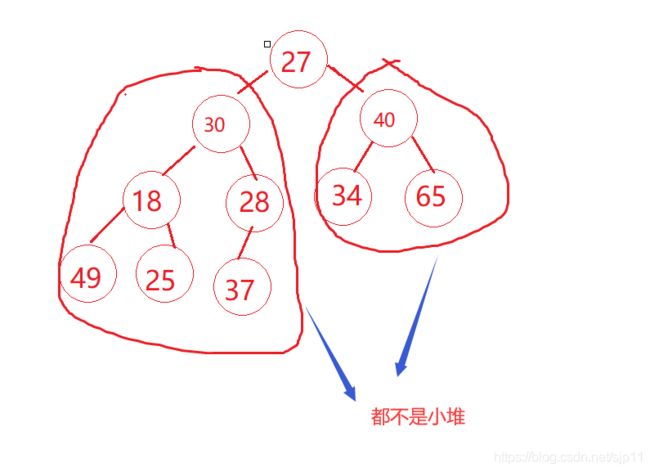
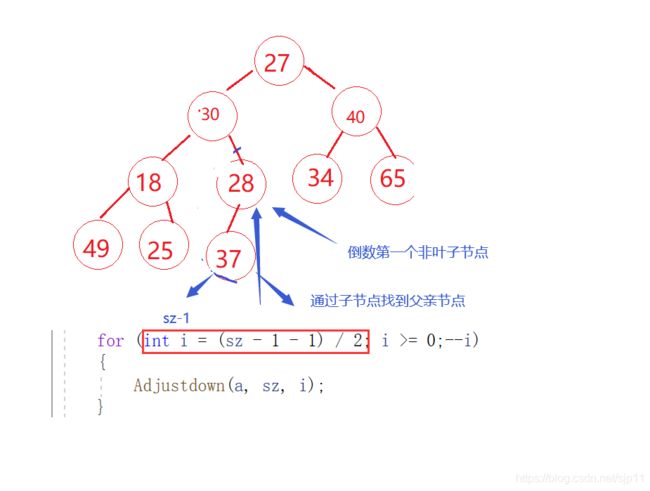
int a[] = {27,30,40,18,28,34,65,49,25,37};
这时候我们就不能使用向下调整的方法,所以我们要想办法把左右子树变成两个小堆
从倒数第一个非叶子节点,从后往前,依次作为子树去向下调整

代码是在上面的基础上,在加一个for循环,所以,我们这样我们就可以把一个无规则的数组变成一个小堆
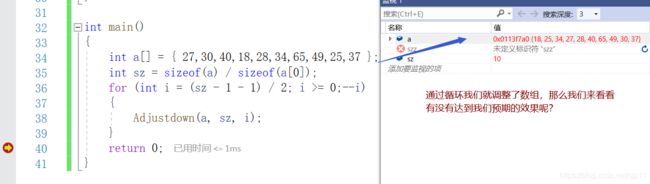
是的,很完美,把一个普通数组变成了一个小根堆
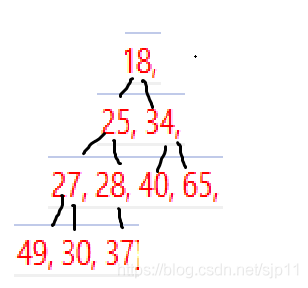
那我们要把一个数组变为一个大根堆,我们需要怎么做:
把一个数组变为大根堆,跟上面的把数组变为小根堆的思路一样,只是左右子树要恰好为大根堆
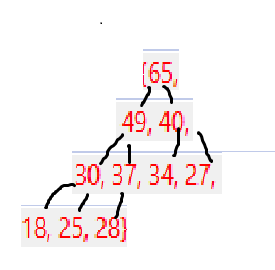
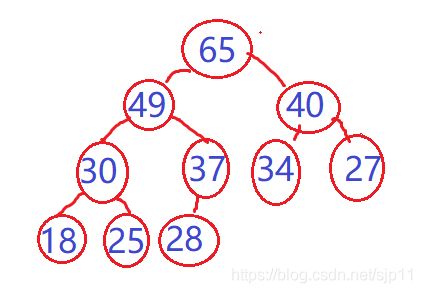
同样的,我们把上面的数组进行调整,把它变成一个大根堆
int a[] = { 27,30,40,18,28,34,65,49,25,37 };
(2)利用堆将数组排一个升序
排序,在c语言中我们学到了一个冒泡排序,而冒泡排序的效率很低,它的时间复杂度为O(N^2)
所以我们可以利用堆的结构进行排序,看一下效率如何
首先,我们要清楚,建堆的时间复杂度为:O(N)
那么我们要排升序,需要利用的是大堆还是小堆呢?哪种效率更高呢
答案:大堆
我们先来看一下小堆的排序:
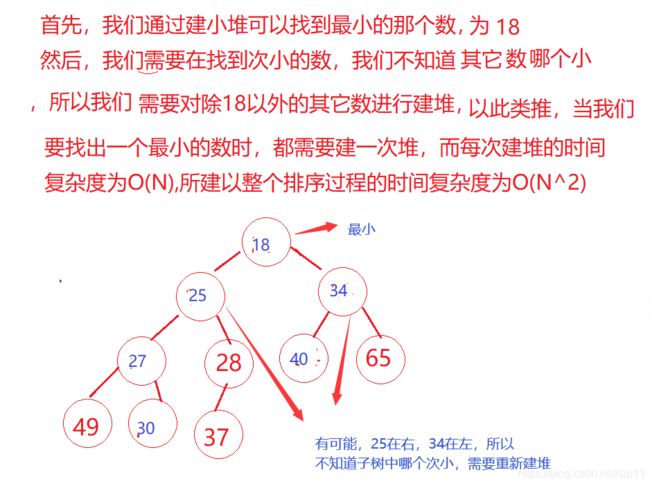
那么,我们来看看建大堆来实现排升序是怎样的呢,
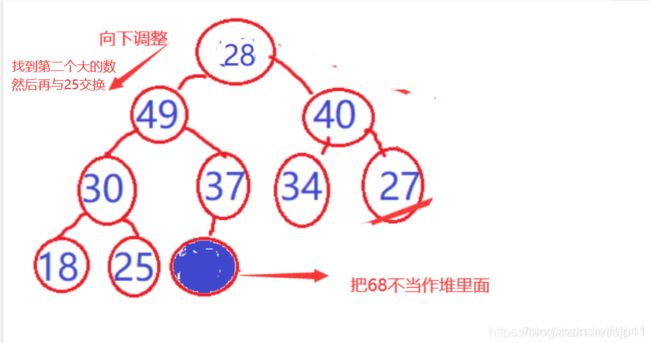
因为根节点是最大值,所以我们把根节点与最后一个值交换,然后不把最后一个值看作堆里面,再对这个堆进行调整,找到第二个大的数
在与最后一个值交换,再调整。。。。直到把数组排序完成。
建堆的时间复杂度为O(N),每个数调整的时间复杂度为O(logN),N个数调整的时间复杂度为O(NlogN),整个排序为的时间复杂度为O(NlogN),所以比效率比冒泡排序高很多
3.堆接口的具体实现
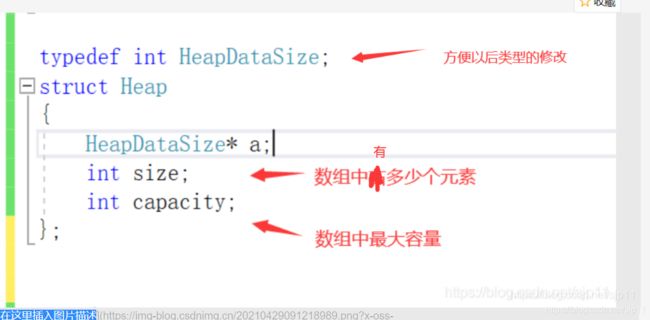
(1)创建堆结构体
首先,我们需要创建一个堆的结构题,用指针方式的来表示数组,可以方便以后malloc和realloc来开辟空间
(2) 堆的初始化
我们要把一个数组中的所有元素拷贝给堆数组,然后再把堆数组初始化为一个大堆
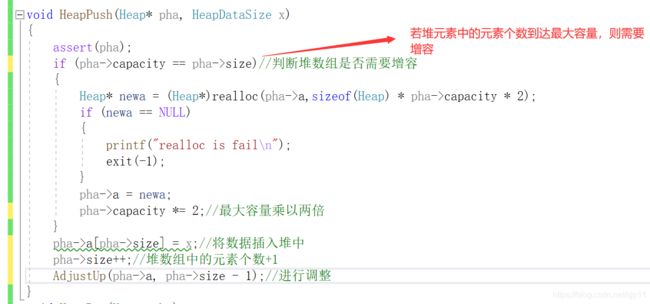
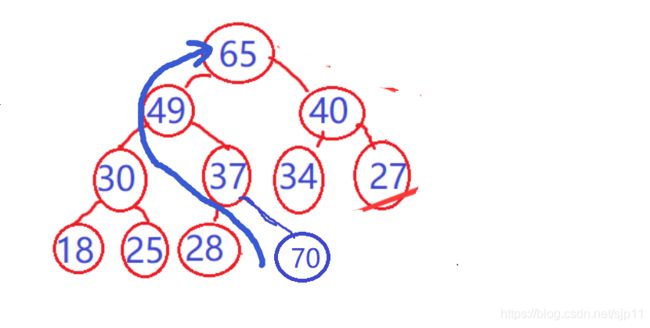
(3)插入数据
当我们在后面插入一个数据后,为了让它保持一个大堆,我们需要将插入的数据进行调整,也就是向上调整函数
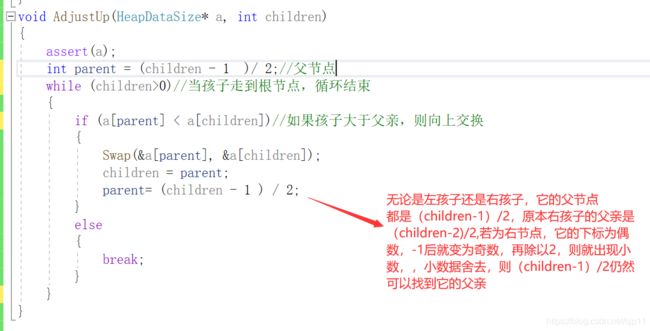
(4)向上调整函数
(5)删除一个数据
我们要将堆顶的第一个数据删除,我们需要先将第一个数据与最后一个数据交换,然后在把最后一个数据删除掉。
最后在把第一数据进行向下调整,这样我们就仍然可以保持我们的大堆
(6)求堆中有多少个数
这个接口很简单,只需要放回size即可