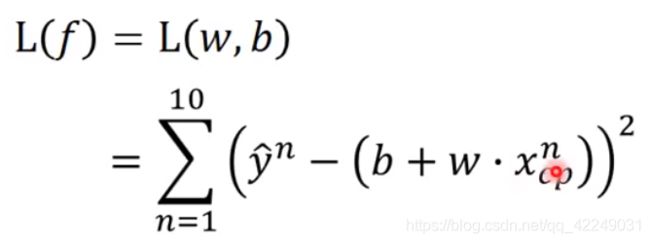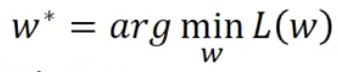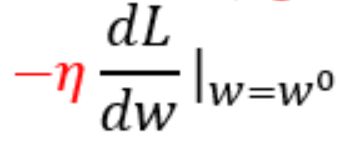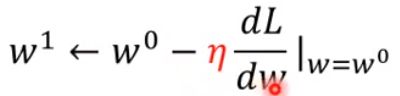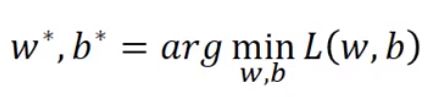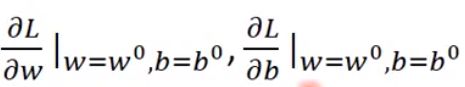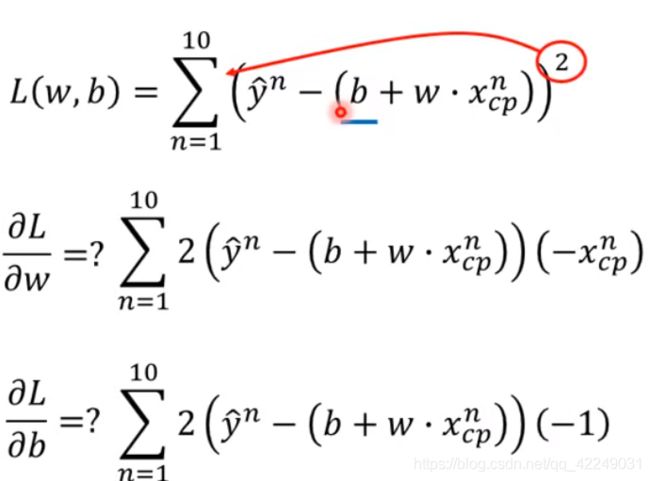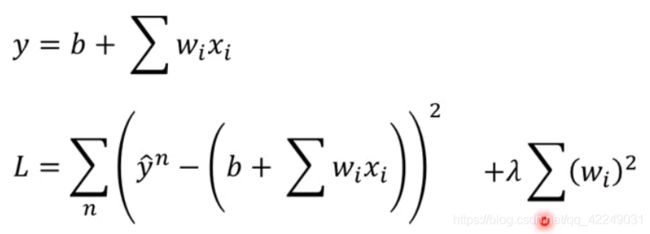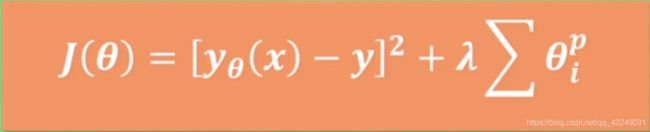李宏毅 机器学习(2017)学习笔记——1-回归

目录

1. Regression（回归）

2. 回归的应用——预测宝可梦的CP值

2.1 步骤一：模型（Model）

2.2 步骤二：函数的评估标准（Goodness of Function）

2.3 步骤三：最优函数（Best Function）

2.3.1 梯度下降法

2.3.2 梯度下降法的缺点

3. 模型的选择

4. 从单变量到多变量

4.1 返回步骤一：重新设计模型

4.2 返回步骤二：正则化

补充：正则化

---

1. Regression（回归）

    回归（Regression）的思想可以用来解决生活中的很多问题。例如股票预测系统——输入历史股票走势，输出今天的股票指数、无人汽车——输入汽车传感器数据，输出方向盘角度、推荐系统——输入使用者和商品的数据，输出购买的可能性。

2. 回归的应用——预测宝可梦的CP值

    任务：根据宝可梦的相关属性预测宝可梦的战斗力

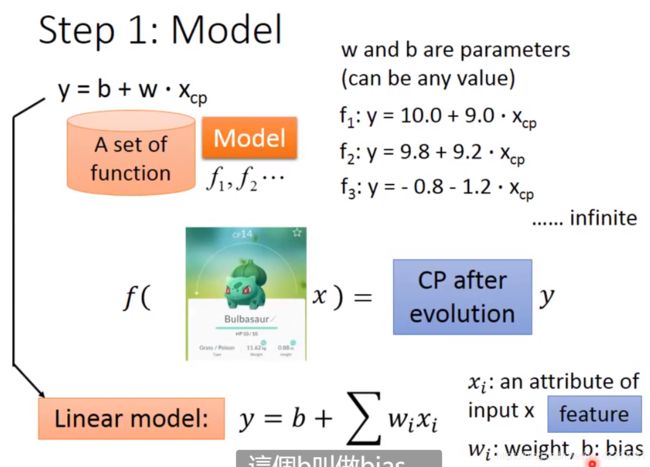
2.1 步骤一：模型（Model）

    函数集就是所谓的模型，函数的输入是宝可梦的特征x，输出是宝可梦的CP值y。

    先假设一个简单的模型（线性模型），我们认为进化后的CP值y等于一个常数b，加上一个参数w乘以进化前的CP值​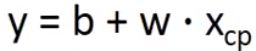，，w和b可以代任何值。我们需要通过训练数据集确定哪一个函数是合理的函数。

    线性模型的通式是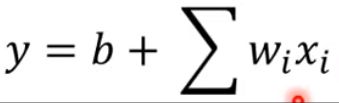，其中表示输入的x的各种属性，叫做特征，叫做权重，b叫做偏移量。

2.2 步骤二：函数的评估标准（Goodness of Function）

    有了训练数据以后，我们就可以定义这个函数的好坏。

    首先定义一个损失函数L（Loss function），损失函数的输入是一个函数，输出是输入函数有多不好。损失函数L是在衡量一组参数b和w的好坏。

    我们通常对损失函数L定义如下：

    里面的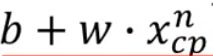（）是我们用函数预测得到的数值，外面的是真正的数值，两者作差取平方，就是估测的误差。最后将误差求和就是损失函数。损失越大，函数越不好。

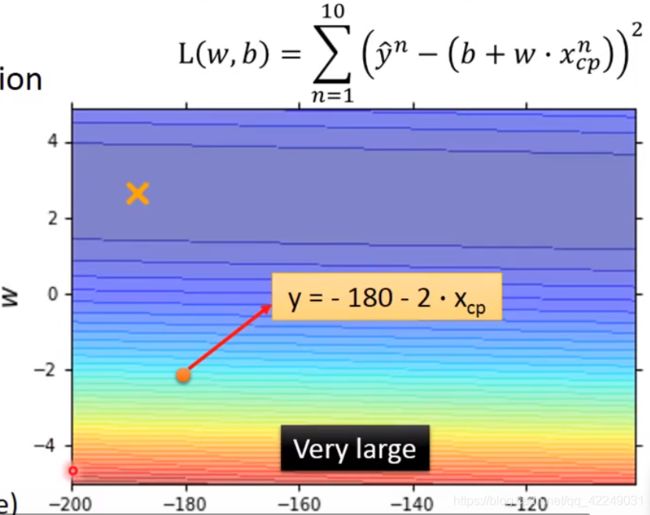
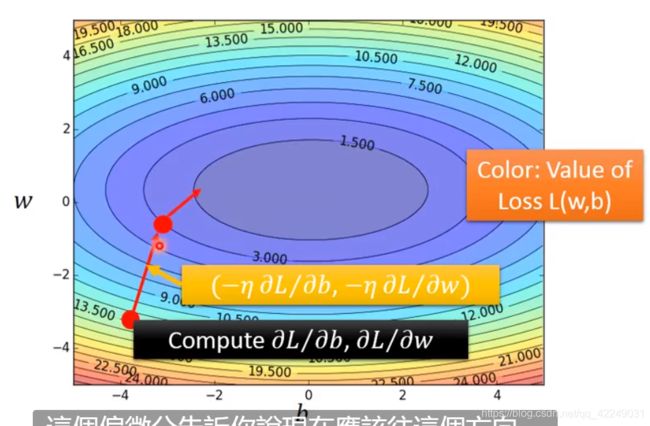
    可以使用等高线图用来衡量函数的好坏，每一个点代表一个函数。

    

2.3 步骤三：最优函数（Best Function）

    寻找最优函数，就是寻找一个f使得L(f)最小。这个让L(f)最小的函数，就是最优函数，写作。

    或者是寻找w和b使得L(w,b)最小，这个w和b就是最好的w和b，写作。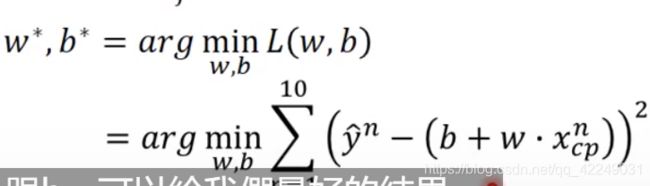

    求最优解，其一可以用线性代数中的最小二乘法；其二使用梯度下降法。

2.3.1 梯度下降法

    梯度下降法的妙处在于，只要L是可微分的，不管L是什么函数，梯度下降法都可以用于处理这个函数。

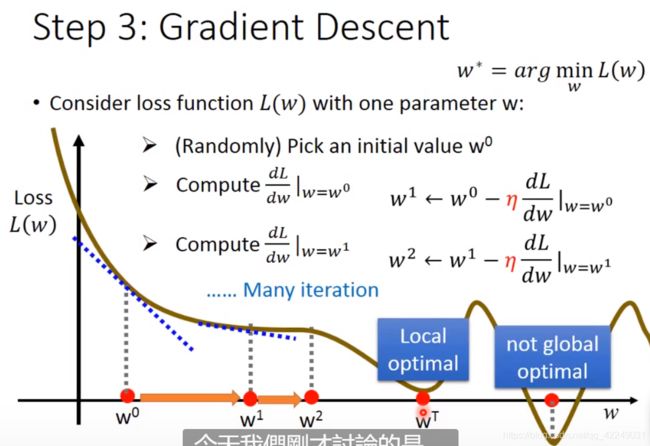
    梯度下降法（只有一个参数）的具体做法如下：

    

    先假设一个简单的L(w)使得。

        ① 随意选取一个初始点。

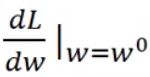        ② 计算在w = 的位置，参数w对于损失函数的微分（切线斜率）。

        若切线斜率为负，左边的损失比右边高，应该增加w的值。

        若切线斜率为正，右边的损失比左面高，应该减小w的值。

        （具体作图更加直观）

        w移动的步长取决于：

        1) 现在的微分值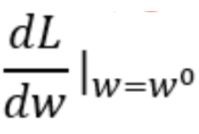的大小（微分值越大越陡峭，移动的距离越大）

        2) 实现定好的学习率η（学习率越大，学习的速度越快）

        更新后的w如下：

        ③ 重复②，计算，并继续更新w。

        经过T次更新取得局部最小值。（在回归中没有局部最小值）

    梯度下降法（有两个参数）的具体做法如下：

        ① 随机选取两个初始值。

        ② 计算在的情况下，w对L的偏微分和b对L的偏微分。

        

        ③ 根据计算结果更新w和b两个参数，。

        重复步骤②，持续更新参数。找到最优w和b。

    梯度下降法中的梯度是指。

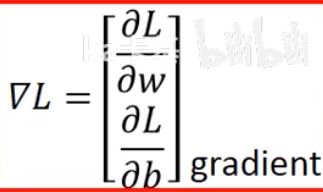
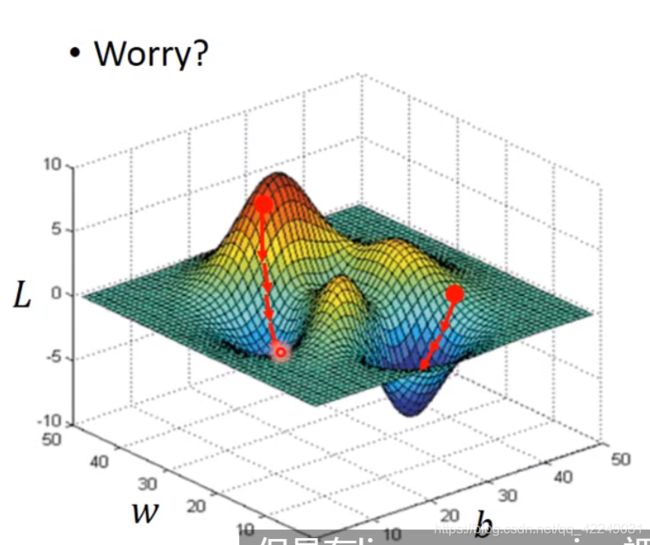
    梯度下降法的可视化（梯度下降的方向就是等高线的法线方向）：

    

2.3.2 梯度下降法的缺点

    

    由于函数的不同，可能会因为初始值的选取而陷入局部最优。

    但是线性回归中无须担心，因为线性回归中不存在局部最优值，任选一组初始值计算的局部最优都是一样的。

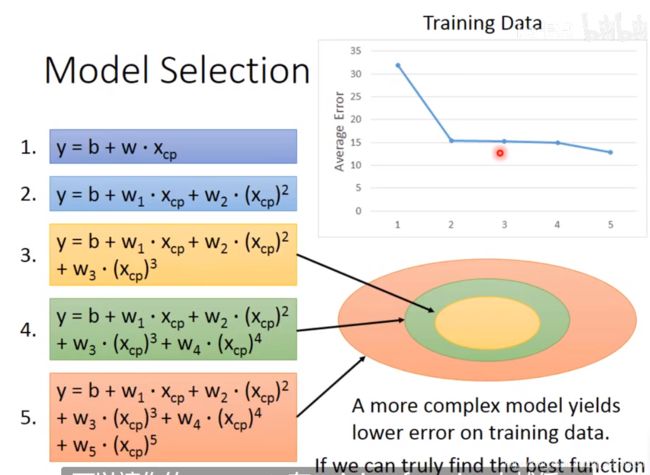
3. 模型的选择

    通过三个步骤训练出线性函数并求出损失值，但是将测试集代入后，发现结果不如人意，所以考虑模型可能比线性模型更复杂。考虑二次式，三次式，四次式，五次式等。

    

    （在训练集上模型越复杂，损失值越来越小）

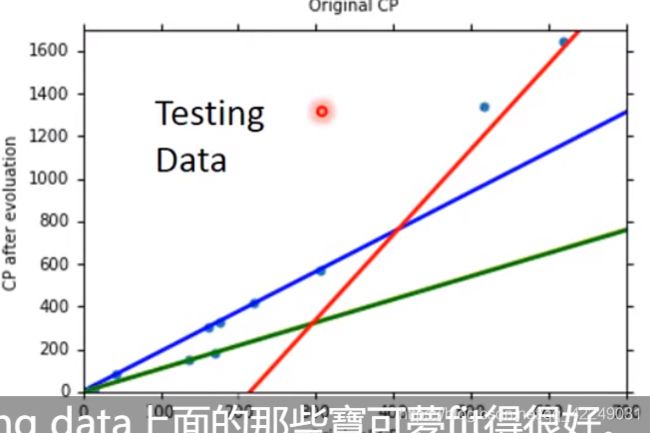
    越复杂的模型在训练集上有更好的效果，但是在测试集上未必有更好的结果。这叫做过拟合。

    

    （如图所示，我们应该选取三次式作为模型）

4. 从单变量到多变量

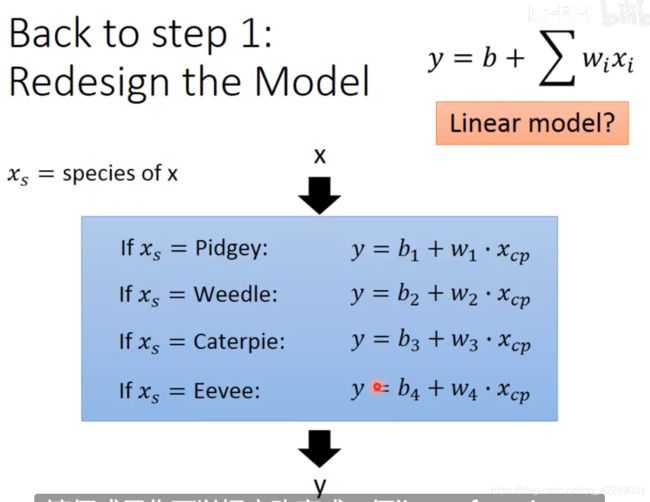
4.1 返回步骤一：重新设计模型

    

    物种不同对应的w和b不同，我门把函数可改成下面这样：

    

    这样更改后，不同种类的宝可梦使用的参数就不一样，对应的函数图像也是不一样的。测试集的图像也拟合的更好，误差很小。

    可以宝可梦的体重，身高，HP值都加入自变量中：

    

    此时得到一个误差很低的模型，但是由于过拟合，在测试集上得到了一个很高的误差。

4.2 返回步骤二：正则化

    重新定义损失函数，额外加上一项。

    

    我们期待得到参数值w越小越好，这是因为参数值接近0的函数是比较平滑的。

    平滑是指：当输入变化时，输出的变化不敏感。（平滑的函数能够很好地抗干扰）

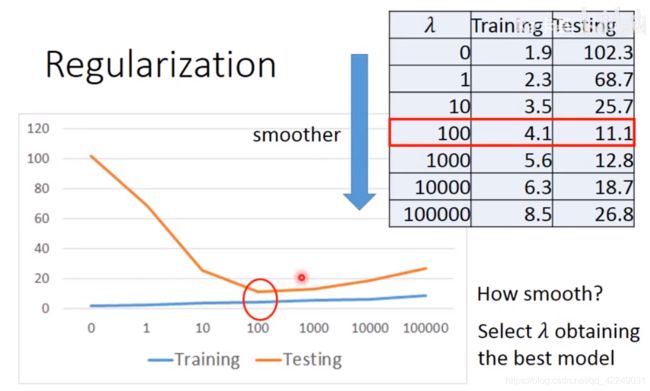
    当λ值越大，说明考虑平滑得正则化项影响力越大，对应的函数越平滑。

    函数越平滑，在训练集上得到的误差越大，而早测试集上的误差可能越小。

       

    我们希望我们找到的函数是平滑的，又不能太平滑而接近一条水平线，所以我们应该调整λ的值而得到最好的模型。（如上图的转折点就是最好的λ值）

    注：在做回归时不需要考虑偏移项。

 

补充：正则化

    学习的过程中对正则化的理解不是很透彻，所以学习了另一个视频。

什么是 L1 L2 正规化 正则化 Regularization (深度学习 deep learning)_哔哩哔哩 (゜-゜)つロ 干杯~-bilibili

    正则化是用于减缓过拟合问题的。

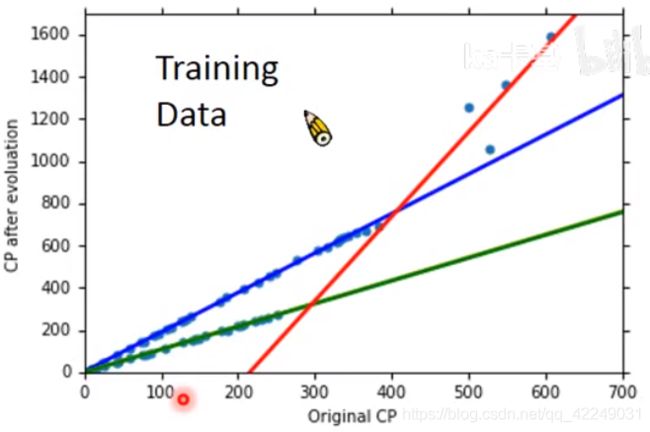
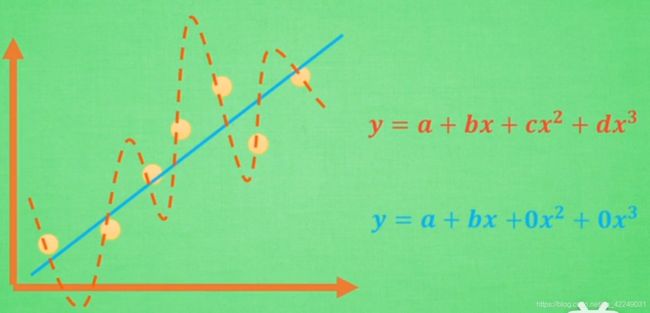
    过拟合是指模型对可见数据的过度自信，非常完美的拟合了这些数据。通常，具备过拟合能力的方程都是很复杂的非线性方程。

    

    如图所示，虽然蓝色方程的误差大于红色方程，但是蓝色方程对于数据的特征有着更好的概括能力。为了能更好的学习到这些参数，引入了L1和L2正则化。

    通常，函数的误差是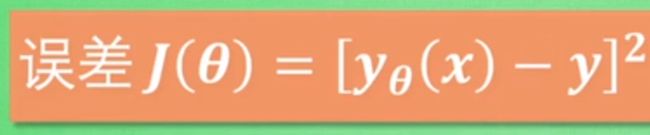，而具体是L1还是L2正则化，取决于后面的一项。

    如果加的是参数平方和，则是L2正则化。            

    如果加的是参数的绝对值和，则是L1正则化。

    正则化的工作原理：

    以L2正则化为例，机器学习的过程是通过改变参数θ来减小误差的过程。在这一过程中，非线性越强的参数（例如）修改的越多（因为可以使得函数图像更曲折来拟合每一个数据点）。

    

    而正则化就是用于控制参数的变化的。

    L1正则化和L2正则化的不同：

    

    正则化方程就是在黄线上产生的额外误差，也可理解为惩罚度。黄线和蓝线交点上的点可以让两个误差的和最小。

    （L1的解不稳定）

    为了控制正则化的程度，乘上一个参数λ，用p来代表对参数的正则化程度。