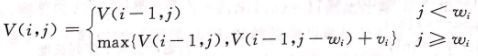Python实现动态规划01背包问题

代码：https://blog.csdn.net/qq_34178562/article/details/79959380

理论讲解：

https://www.bilibili.com/video/BV1K4411X766?from=search&seid=13724711054890720316

https://www.bilibili.com/video/BV1XD4y1S7nv?from=search&seid=13724711054890720316

 

先假设一个数据输入：六个东西，东西A重2kg价值2毛钱，东西B重2kg价值3毛钱，东西C重3kg价值1毛钱，东西D重1kg价值5毛钱，东西E重5kg价值4毛钱，东西F重2kg价值3毛钱。问容量10kg书包最多能装几毛钱的东西。

这个问题需要建立一个动态规划表，能理解这个表的建立过程就能知道代码怎么写。

价值（毛）	0kg	1kg	2kg	3kg	4kg	5kg	6kg	7kg	8kg	9kg	10kg
不放东西	0	0	0	0	0	0	0	0	0	0	0
A w=2 v=2	0	0	2	2	2	2	2	2	2	2	2
B w=2 v=3	0	0	3	3	5	5	5	5	5	5	5
C w=3 v=1	0	0	3	3	5	5	5	6	6	6	6
D w=1 v=5	0	5	5	8	8	10	10	10	11	11	11
E w=5 v=4	0	5	5	8	8	10	10	10	12	12	14
F w=2 v=3	0	5	5	8	8	11	11	13	13	13	15

首先，如果我们不放东西，背包肯定没有价值，所以不放东西这一排为0。背包容量为0，放不进去东西，背包也没有价值，所以0kg这一列为0。

然后，我们对应公式来看：V(i,j)表示将前i个物品放进容量为j的背包。

1）我们看A这一排，(A,1kg)等于0，为什么等于0，1kg小于A的重量2kg，符合j<wi，所以(A,1kg)等于(A,0kg)，等于0。

2）我们看(A,2kg)等于2，为什么等于2，2kg等于A的重量2kg，符合j>=wi，所以(A,2kg)等于max( (不放东西,2kg), (不放东西,2kg-2kg)+A的价值 )，即max(0, 0+2)=2。

3）我们看A这一排的后面，由于i不变，max的前一项永远是(不放东西,*)=0，max的后一项永远是(不放东西,*)+A的价值=2，所以A这一排后面全是2。

细品

4）我们看(B,1kg)等于0，为什么等于0，1kg小于B的重量2kg，符合j<wi，所以(B,1kg)等于(B,0kg)，等于0。

5）我们看(B,2kg)等于3，为什么等于3，2kg等于B的重量2kg，符合j>=wi，所以(B,2kg)等于max( (A,2kg), (A,2kg-2kg)+B的价值 )，即max(2, 0+3)=3。

6）我们看(B,4kg)等于5，为什么等于5，4kg大于B的重量2kg，符合j>=wi，所以(B,4kg)等于max( (A,4kg), (A,4kg-2kg)+B的价值 )，即max(2, 2+3)=5。

对比着品

7）我们看(D,1kg)等于5，为什么等于5，1kg等于D的重量1kg，符合j>=wi，所以(D,1kg)等于max( (C,1kg), (C,1kg-1kg)+D的价值 )，即max(0, 0+5)=5。

8）我们看(F,10kg)，10kg大于F的重量2kg，符合j>=wi，所以(F,10kg)等于max( (E,10kg), (E,10kg-2kg)+F的价值 )，即max(14, 12+3)=15。

最后，问题的答案既是10kg背包能装最多1块5毛钱的东西。

 

保存一份代码，牢记公式，分清楚代码里面的i 和j 是啥就行。

def bag(n, c, w, v):
    """
    测试数据：
    n = 6  物品的数量，
    c = 10 书包能承受的重量，
    w = [2, 2, 3, 1, 5, 2] 每个物品的重量，
    v = [2, 3, 1, 5, 4, 3] 每个物品的价值
    """
    #置零，表示初始状态
    value = [[0 for j in range(c + 1)] for i in range(n + 1)]
    for i in range(1, n + 1):
        for j in range(1, c + 1):

            #
            value[i][j] = value[i - 1][j]

            #
            if j >= w[i - 1] and value[i][j] < value[i - 1][j - w[i - 1]] + v[i - 1]:
                value[i][j] = value[i - 1][j - w[i - 1]] + v[i - 1]

    #打印动态规划表
    for x in value:
        print(x)

    return value

#w = list(map(int,input().split(' ')))
#v = list(map(int,input().split(' ')))
#c = eval(input())

w = [2, 2, 3, 1, 5, 2]
v = [2, 3, 1, 5, 4, 3]
c = 10
n = len(v)
print('{}'.format(bag(n,c,w,v)[n][c]))