Pytorch-线性回归(一)

一.线性回归

1.数学概念

线性回归是利用数理统计中的回归分析，来确定两种，或两种以上变量关系的一种统计方法。简而言之，对于输入$x$与输出$y$有一个映射$f$,$y=f(x)$,$f$的形式为$wx+b$,其中$w,b$为可调参数，训练$w,b$

线性模型$$y=f_w(x)=w_0+\sum _{i=1}^n{w}_i{x}_{i}x=w^{T}x$$

$$x=(1,x_1,x_2\cdot \cdot \cdot \cdot x_n)$$

2 .损失函数 loss function

$$\underset{w}{\min }\frac{1}{N}\sum _{i=1}^N\mathcal{L}(y_i,f_w(x_i))$$

$$MSE:\mathcal{L}(y_i,f_w(x_i))=\frac{1}{2}(y_i-f_w(x_i){)}^2$$

3.梯度更新

3.1 批量梯度下降算法Batch Gradient Descent

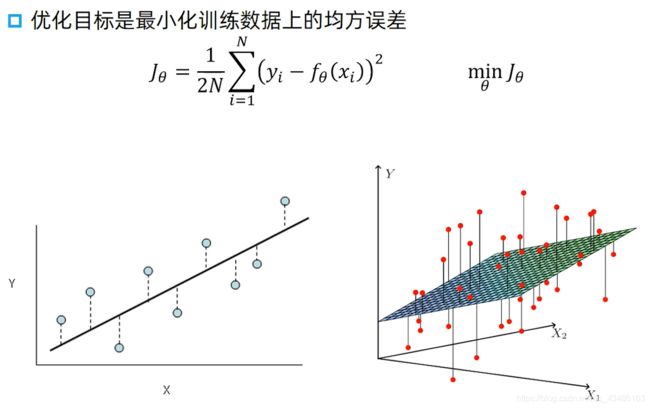
优化函数
$$J(w)=\frac{1}{2N}\sum _{i=1}^N(y_i-f_w(x_i){)}^2\underset{w}{\min }J(w)$$
根据整个批量数据的梯度更新参数 $w_{new}=w_{old}-\eta \frac{\partial J(w)}{\partial w}$
$$\begin{array}{rl}\frac{\partial J(w)}{\partial w}& =-\frac{1}{N}\sum _{i=1}^N((y_i-f_w(x_i)\frac{\partial f_w(x_i)}{\partial w})\\ & =-\frac{1}{N}\sum _{i=1}^N(y_i-f_w(x_i)x_i\end{array}$$

$$w_{new}=w_{old}+\eta \frac{1}{N}\sum _{i=1}^N(y_i-f_w(x_i)x_i$$

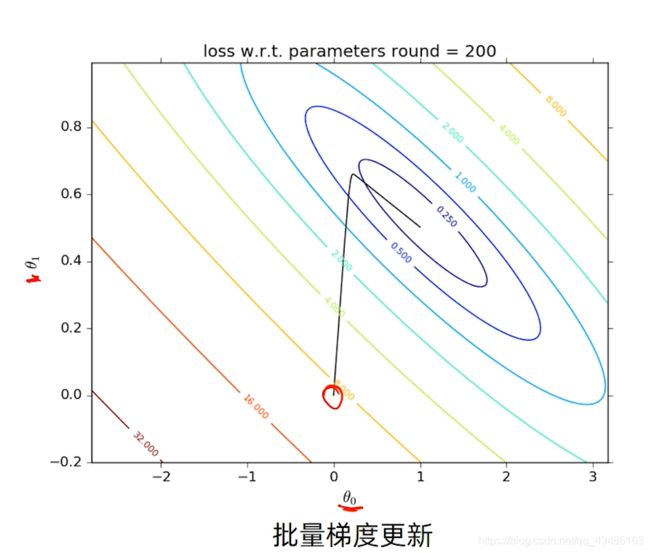
3.2 随机梯度下降Stochastic Gradient Descent

优化函数
$$J^{(i)}(w)=\frac{1}{2}(y_i-f_w(x_i){)}^2\underset{w}{\min }\frac{1}{N}\sum _i{J}^{(i)}(w)$$
根据整个批量数据的梯度更新参数 $w_{new}=w_{old}-\eta \frac{\partial J(w)}{\partial w}$
$$\begin{array}{rl}\frac{\partial J^{(i)}(w)}{\partial w}& =-(y_i-f_w(x_i)\frac{\partial f_w(x_i)}{\partial w})\\ & =-(y_i-f_w(x_i))x_i\end{array}$$

$$w_{new}=w_{old}+\eta (y_i-f_w(x_i))x_i$$

3.3 小批量梯度下降Mini-Batch Gradient Descent

批量梯度下降和随机梯度下降的结合

1.将整个训练集分成K个小批量（mini-batches）
$$\left\{1，2，3,\cdots ，k\right\}$$

2.对每一个小批量$k$,做一个批量下降来降低
$$J^{(k)}(w)=\frac{1}{2N_k}\sum _{i=1}^{N_k}(y_i-f_w(x_i){)}^2$$

3.对于每一个小批量，更新参数
$$w_{new}=w_{old}-\eta \frac{\partial J^{(k)}(w)}{\partial w}$$

未完待续----------------------------------------------------------------------------------------------------------
后期比较优化算法