NumPy基础学习笔记
目录
- 一、NumPy简介与安装使用介绍
-
- 1.1 NumPy的简介
- 1.2 Numpy的安装与使用
- 1.3 NumPy常用数据类型介绍
- 二、NumPy数组与矩阵的创建
-
- 2.1 NumPy基本数组的创建
-
- 2.1.1 一维数组的创建
- 2.1.2 二维及高维数组的创建
- 2.1.3 添加、删除和排序元素
- 2.1.4 重塑阵列
- 2.1.5 如何向数组中添加新的轴
- 2.1.6 索引切片
- 2.1.7 从现有数据创建数组
- 2.2 NumPy基本数组运算与广播
-
- 2.2.1 数组之间的运算
- 2.2.2 数组的广播
- 2.2.3 有用的数组操作
- 2.3 NumPy矩阵的创建
-
- 2.3.1 常用矩阵创建
- 2.3.2 矩阵索引和切片
- 2.3.3 矩阵统计计算
- 2.3.4 矩阵的变换和重塑
- 2.3.5 矩阵的相关计算
- 三、保存与加载NumPy
一、NumPy简介与安装使用介绍
1.1 NumPy的简介
NumPy是一个基础科学的计算包,极大地简化了向量和矩阵的操作处理,在Python中广泛用于科学计算、数据分析和机器学习。Python 的一些主要软件包(如 scikit-learn、SciPy、pandas 和 tensorflow)都以 NumPy 作为其架构的基础部分。
- NumPy详细介绍
学习参考
1.2 Numpy的安装与使用
- 安装方式:conda install numpy 或者 pip install numpy
- 使用如下代码块所示
# 导入NumPy模块
import numpy as np
a = np.arange(6)
print(a,type(a))
a2 = a[np.newaxis, :]
a2.shape
[0 1 2 3 4 5]
(1, 6)
从以上例子可以看出NumPy数组与列表表面上看形式是一样的,那么它们的区别是什么呢?
- NumPy提供了大量快速高效的方法来创建数组和处理其中的数字数据。
- 虽然Python列表可以在单个列表中包含不同的数据类型,但NumPy数组中的所有元素都应该是同质的。
- 如果数组不是同质的,那么在数组上执行的数学操作将是极其低效的
为什么要使用Numpy?
- NumPy数组比Python列表创建更快、更紧凑。
- 数组占用内存少,使用方便。
- NumPy使用更少的内存来存储数据,它提供了一种指定数据类型的机制。
- 这允许对代码进行进一步优化。
1.3 NumPy常用数据类型介绍
NumPy中可以创建一维数组(1D array )、二维数组(2D array)、N维数组(ndarray)、向量(vector)和矩阵(matrix),此外还有3-D或者高维数组,张量也是常用的。
- 数组的属性是什么?
数组通常是相同类型和大小的项的固定大小容器。数组中的维度和项的数量是由其形状定义的。数组的形状是由指定每个维度大小的非负整数组成的元组。
- 在NumPy中,维度称为轴线。这意味着,如下所示的2D数组:
ndarray.ndim将查询数组的轴数或维数。
ndarray.size将查询数组的元素总数。
ndarray.shape将显示表示沿数组每个维度存储的元素数的整数元组。
import numpy as np
a = np.array([[1,2,3],
[3,4,5],
[3,4,5]])
print(a,type(a),a.shape,a.ndim,a.size)
[[1 2 3]
[3 4 5]
[3 4 5]] (3, 3) 2 9
可以看出这个数组中由两个轴,第一个轴的长度为2,第二个轴的长度为3。可以得出的长度关系,在其他Python容器对象中一样可通过对数组进行索引或切片来访问和修改数组的内容。
二、NumPy数组与矩阵的创建
2.1 NumPy基本数组的创建
2.1.1 一维数组的创建
- 创建NumPy数组,可以使用以下函数np.array()
- 创建一个简单数组所需要做的就是将一个列表传递给它,还可以在列表中指定数据类型。
a = [1,2,3]
print(a,type(a))
b = np.array(a)
print(b,type(b))
[1, 2, 3]
[1 2 3]
可视化是为了简化想法,对NumPy的概念有一个基本的理解。将数组可视化为:
 |
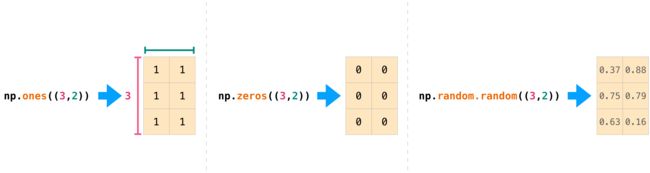
- 全为0的一维数组创建(np.zeros(长度))
np.zeros(2)
array([0., 0.])
- 全为1的一维数组创建(np.ones(长度))
np.ones(2)
array([1., 1.])
- 空数组的创建(np.empty(长度))
empty创建一个数组,其初始内容是随机的,取决于内存的状态。用于填充计算出的新数组。
a = np.empty(2)
print(a)
[1. 1.]
- 等差数列的数组。它包含一个间隔均匀的范围需要指定第一数, 最后数,以及台阶尺寸。
# 列表中
list1 = range(1,10,2)
list1 = [i for i in list1]
print(list1,type(list1))
# 数组中
nd_ = np.arange(1, 10, 2)
print(nd_,type(nd_))
[1, 3, 5, 7, 9]
[1 3 5 7 9]
# 只需指定一个数也可以,其台阶默认为1
np.arange(10)
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
- 使用np.linspace(初始,终止,num=份数)创建具有在指定间隔内线性排列的值的数组
np.linspace(0, 10, num=5)
array([ 0. , 2.5, 5. , 7.5, 10. ])
- 指定数据类型【更多数据类型参考】
默认数据类型为浮点(np.float64),可以使用dtype关键词。
np.ones(2, dtype=np.int64)
array([1, 1], dtype=int64)
np.ones(2, dtype=np.str)
array(['1', '1'], dtype='2.1.2 二维及高维数组的创建
实质上就是多个一维数组通过堆叠等形式形成的。
# 一般高维数组的创建
x = np.array([[1, 2], [3, 4]])
print(x,'\n',type(x),'\n',x.shape,'\n',x.size)
[[1 2]
[3 4]]
(2, 2)
4
a = np.array([1, 2, 3, 4])
b = np.array([5, 6, 7, 8])
# 垂直堆叠
c = np.vstack((a, b))
d = np.hstack((a, b))
print(c,type(c),c.shape,c.size)
print('\n',d,type(d),d.shape,d.size)
[[1 2 3 4]
[5 6 7 8]] (2, 4) 8
[1 2 3 4 5 6 7 8] (8,) 8
2.1.3 添加、删除和排序元素
- 添加【np.concatenate((a, b))】
# 一维数组的添加,只能是行添加
a = np.array([1, 2, 3, 4])
b = np.array([5, 6, 7, 8])
np.concatenate((a, b), axis=0)
array([1, 2, 3, 4, 5, 6, 7, 8])
# 多维数组的添加,可行可列,单注意数组形状行数或者列数是否相同
x = np.array([[1, 2], [3, 4]])
y = np.array([[5, 6]])
np.concatenate((x, y), axis=0)
array([[1, 2],
[3, 4],
[5, 6]])
x = np.array([[1, 2], [3, 4]])
y = np.array([[5, 6],[7,8]])
np.concatenate((x, y), axis=1)
array([[1, 2, 5, 6],
[3, 4, 7, 8]])
- 删除元素,可以转变思路,即根据索引提取需要的元素,抛弃不需要的。
# 一维数组
a = np.array([1, 2, 3, 4])
print(a.shape)
a[2:3]
(4,)
array([3])
# 二维数组 x[行选取范围][列选取范围]
x = np.array([[1, 2,3], [3, 4,5]])
print(x.shape)
x[:][:1]
(2, 3)
array([[1, 2, 3]])
- 排序
对元素排序用【np.sort()】。在调用函数时,可以指定轴、种类和顺序。
arr = np.array([2, 1, 5, 3, 7, 4, 6, 8])
np.sort(arr)
array([1, 2, 3, 4, 5, 6, 7, 8])
a = np.array([[1,4],[3,1]])
# 默认按各行排序
print(np.sort(a))
# 不指定坐标轴,结果为一维数组
print(np.sort(a, axis=None))
# 指定按列排序设置axis=0,行为axis=1
print(np.sort(a, axis=0))
[[1 4]
[1 3]]
[1 1 3 4]
[[1 1]
[3 4]]
np.searchsorted()查询位置(只针对一维数组)方法
# 默认左边开始计数
a = np.searchsorted([1,2,4,3,5], 4)
print(a)
# 指定右边查询元素的位置
a = np.searchsorted([1,2,7,3,4,5], 3, side='right')
print(a)
2
4
numpy.partition()局部排序方法
a = np.array([3, 4, 2, 1])
np.partition(a, 3)
array([2, 1, 3, 4])
np.partition(a, (1, 3))
array([1, 2, 3, 4])
此外还有方法见它是沿着指定的轴间接排序的、对多个键的间接稳定排序等方法。
2.1.4 重塑阵列
使用【array.reshape(行数,列数)】将在不更改数据的情况下为数组提供新的形状。请记住,当您使用RESTPE方法时,要生成的数组需要有与原始数组相同数量的元素。如果从包含12个元素的数组开始,则需要确保新数组中总共有12个元素。
使用np.reshape(重塑的数组,新的形状,order = 索引顺序)方法
- 'C’指定按行顺序
- 'F’指定按列顺序
a = np.arange(6)
b = a.reshape(3, 2,order='F')
print(a,'\n\n',b)
[0 1 2 3 4 5]
[[0 3]
[1 4]
[2 5]]
a = np.arange(6)
b = a.reshape(3, 2,order='C')
print(a,'\n\n',b)
[0 1 2 3 4 5]
[[0 1]
[2 3]
[4 5]]
np.reshape(a, newshape=(3, 2), order='F')
array([[0, 3],
[1, 4],
[2, 5]])
np.reshape(a, newshape=(3, 2), order='C')
array([[0, 1],
[2, 3],
[4, 5]])
2.1.5 如何向数组中添加新的轴
使用np.newaxis和np.expand_dims可增加现有数组的维度。使用np.newaxis使用一次时,数组的维数将增加一个维度。这意味着1D数组将成为二维空间数组,二维空间数组将成为三维空间数组等等。
- np.newaxis用法
a = np.array([1, 2, 3, 4, 5, 6])
a.shape
(6,)
# 用np.newaxis添加新轴
a2 = a[np.newaxis, :]
print(a2,a2.shape)
[[1 2 3 4 5 6]] (1, 6)
a3 = a2[np.newaxis, :]
print(a3,a3.shape)
[[[1 2 3 4 5 6]]] (1, 1, 6)
# 对于列向量,可以沿第二纬度插入新轴
col_vector = a[:, np.newaxis]
print(col_vector,col_vector.shape)
[[1]
[2]
[3]
[4]
[5]
[6]] (6, 1)
- np.expand_dims用法
b = np.expand_dims(a, axis=0)
print(b,'\n\n',b.shape)
b = np.expand_dims(a, axis=1)
print('\n\n',b,'\n\n',b.shape)
[[1 2 3 4 5 6]]
(1, 6)
[[1]
[2]
[3]
[4]
[5]
[6]]
(6, 1)
axis=还可以是元组
y = np.expand_dims(a, axis=(1, 0))
y
array([[[1, 2, 3, 4, 5, 6]]])
y = np.expand_dims(a, axis=(2, 0))
y
array([[[1],
[2],
[3],
[4],
[5],
[6]]])
2.1.6 索引切片
- 索引取值
data = np.array([1, 2, 3])
print(data.shape)
print(data[1])
print(data[0:2])
print(data[1:])
print(data[-2:])
(3,)
2
[1 2]
[2 3]
[2 3]
如果要将数组或特定数组元素的一部分用于进一步的分析或其他操作,需要对数组进行子集、切片和/或索引。如果要从满足特定条件的数组中选择值,则使用NumPy非常简单。
 |
- 按条件取值
a = np.array([[1, 2, 3, 5], [5, 2, 7, 8], [2, 10, 11, 12]])
# 筛选小于5的数据
print(a[a < 5])
[1 2 3 2 2]
# 筛选大于5的数据
five_up = (a >= 5)
print(a[five_up])
[ 5 5 7 8 10 11 12]
# 能被2整除的数据
divisible_by_2 = a[a%2==0]
print(divisible_by_2)
[ 2 2 8 2 10 12]
# 大于2并且小于11的数据
c = a[(a > 2) & (a < 11)]
print(c)
[ 3 5 5 7 8 10]
# 位运算符为了返回指定数组中的值是否满足特定条件的布尔值
five_up = (a > 5) | (a == 5)
print(five_up)
[[False False False True]
[ True False True True]
[False True True True]]
- 【np.nonzero()】从数组中选择元素或索引
a = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
# 获取小于5的元素的索引
b = np.nonzero(a < 5)
print(b)
# 若要提取数组中小于5的元素
print('\n',a[b])
(array([0, 0, 0, 0], dtype=int64), array([0, 1, 2, 3], dtype=int64))
[1 2 3 4]
# 如果要查找的元素不存在于数组中,则返回的索引数组将为空。
not_there = np.nonzero(a == 42)
print(not_there)
(array([], dtype=int64), array([], dtype=int64))
更多索引切片详细参考
2.1.7 从现有数据创建数组
a = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
- 通过切片创建新数组
arr1 = a[3:8]
arr1
array([4, 5, 6, 7, 8])
- 堆叠创建新数组
a1 = np.array([[1, 1],
[2, 2]])
a2 = np.array([[3, 3],
[4, 4]])
# 水平堆叠
print(np.hstack((a1, a2)),'\n')
# 垂直堆叠
print(np.vstack((a1, a2)))
[[1 1 3 3]
[2 2 4 4]]
[[1 1]
[2 2]
[3 3]
[4 4]]
用np.hsplit可以将数组拆分为几个较小的数组,可以指定要返回的等形数组的数目或列。
x = np.arange(1, 25).reshape(2, 12)
print(x)
np.hsplit(x, 3)
[[ 1 2 3 4 5 6 7 8 9 10 11 12]
[13 14 15 16 17 18 19 20 21 22 23 24]]
[array([[ 1, 2, 3, 4],
[13, 14, 15, 16]]), array([[ 5, 6, 7, 8],
[17, 18, 19, 20]]), array([[ 9, 10, 11, 12],
[21, 22, 23, 24]])]
# 在第三列和第四列之后拆分数组
np.hsplit(x, (3, 5))
[array([[ 1, 2, 3],
[13, 14, 15]]), array([[ 4, 5],
[16, 17]]), array([[ 6, 7, 8, 9, 10, 11, 12],
[18, 19, 20, 21, 22, 23, 24]])]
- 用copy方法将生成数组及其数据的完整副本(深拷贝)
y = x.copy()
y
array([[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12],
[13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24]])
【更多请参考】
2.2 NumPy基本数组运算与广播
2.2.1 数组之间的运算
当我们创建好了数组,就可以开始使用它们了。例如,假设创建了两个数组,一个称为“data”,另一个称为“ones”。
 |
数组一般的运算就是加减乘除四种,对于数组都是对应位置相加减乘除。
- 加法运算
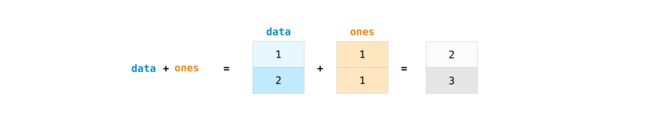 |
data = np.array([1, 2])
ones = np.ones(2, dtype=int)
data + ones
array([2, 3])
- 减法、乘法和除法
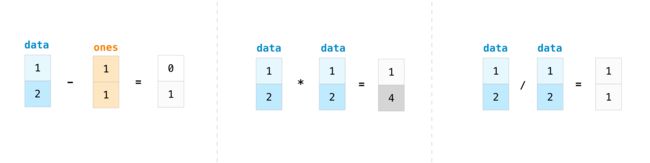 |
print(data - ones)
print(data * data)
print(data / data)
[0 1]
[1 4]
[1. 1.]
- 如果要查找数组中元素的和,可以使用sum()方法,适用于一维数组、二维数组和高维数组。
data.sum()
3
a = np.array([[[1,2],
[2,1]]])
print(a.shape,a.sum())
(1, 2, 2) 6
- 若要在2D数组中求行或列和,通过指定轴计算。
b = np.array([[1, 2], [3, 4]])
print(b,b.shape,b.sum())
# 求列和
print(b.sum(axis=0))
# 求行和
print(b.sum(axis=1))
[[1 2]
[3 4]] (2, 2) 10
[4 6]
[3 7]
2.2.2 数组的广播
有时希望在数组和单个数字之间执行操作(也称为向量和标量之间的运算)或两个不同大小的数组之间。
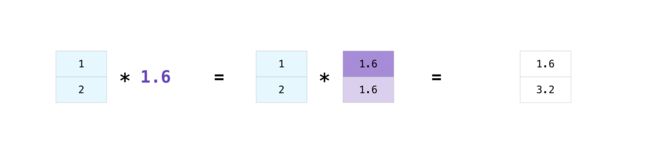 |
data = np.array([1.0, 2.0])
data * 1.6
array([1.6, 3.2])
NumPy数组中每个元素都进行计算,这个概念叫做广播。广播是一种允许NumPy对不同形状的数组执行操作的机制,但数组的维度必须兼容。例如,当两个数组的维数相等或其中一个数组的维数为1时。
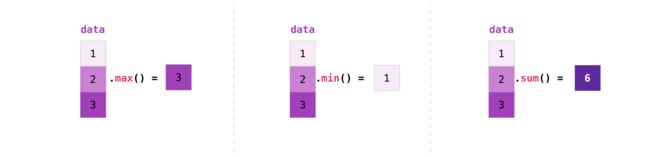
2.2.3 有用的数组操作
data = np.array([1,2,3])
# 最大值
print(data.max())
# 最小值
print(data.min())
# 求和
print(data.sum())
# 平均值
print(data.mean())
# 各元素相乘
print(data.prod())
# 求标准差
print(data.std())
3
1
6
2.0
6
0.816496580927726
 |
a = np.array([[0.45053314, 0.17296777, 0.34376245, 0.5510652],
[0.54627315, 0.05093587, 0.40067661, 0.55645993],
[0.12697628, 0.82485143, 0.26590556, 0.56917101]])
# 求总和
print(a.sum())
# 求总最大值
print(a.max())
# 求总最小值
print(a.min())
# 求总平均值
print(a.mean())
# 求总标准差
print(a.std())
# 求列和
print(a.sum(axis = 0))
# 求行和
print(a.sum(axis = 1))
# 列最小值
print(a.min(axis=0))
# 行最小值
print(a.min(axis=1))
# 列最大值
print(a.max(axis=0))
# 行最大值
print(a.max(axis=1))
# 求列平均值
print(a.mean(axis=0))
# 求行平均值
print(a.mean(axis=1))
# 求列标准差
print(a.std(axis=0))
# 求行标准差
print(a.std(axis=1))
4.8595784
0.82485143
0.05093587
0.4049648666666667
0.21392120766089617
[1.12378257 1.04875507 1.01034462 1.67669614]
[1.51832856 1.55434556 1.78690428]
[0.12697628 0.05093587 0.26590556 0.5510652 ]
[0.17296777 0.05093587 0.12697628]
[0.54627315 0.82485143 0.40067661 0.56917101]
[0.5510652 0.55645993 0.82485143]
[0.37459419 0.34958502 0.33678154 0.55889871]
[0.37958214 0.38858639 0.44672607]
[0.1794018 0.33973673 0.05524104 0.00759016]
[0.14001164 0.2044509 0.27060466]
更多内容参考
2.3 NumPy矩阵的创建
NumPy是对多维数组的运算,默认情况并不运算矩阵。矩阵实质上NumPy数组对象的二维数组对象。Numpy中,矩阵计算是针对整个矩阵中每个元素进行的,与用for循环相比,其在运算速度上更快。
2.3.1 常用矩阵创建
- 向量的创建(单行或单列矩阵)
# 行向量
a = np.array([[1,2,3,4]])
print(a)
# 列向量
print(a.T)
[[1 2 3 4]]
[[1]
[2]
[3]
[4]]
- 通用矩阵创建
data = np.array([[1,2],
[3,4]])
print(data,type(data),data.shape)
[[1 2]
[3 4]] (2, 2)
 |
#创建numpy矩阵
#使用分号隔开数据
matr1=np.mat('1 2 3;4 5 6;7 8 9')
#调用mat和matrix等价
matr2=np.matrix([[1,2,3],[4,5,6],[7,8,9]])
print(matr1,'\n\n',matr2)
[[1 2 3]
[4 5 6]
[7 8 9]]
[[1 2 3]
[4 5 6]
[7 8 9]]
# 一维数组通过reshape创建矩阵
a = np.arange(16,step = 2)
print(a)
# reshape 转换数组的形状
print(a.reshape(4,2))
[ 0 2 4 6 8 10 12 14]
[[ 0 2]
[ 4 6]
[ 8 10]
[12 14]]
- 分块矩阵
arr1 = np.array([[1,2]])
arr2 = np.array([[1,2]])
arr3 = np.array([[1,2]])
arr4 = np.array([[1,2]])
#block-matrix实现分块矩阵创建,即小矩阵组合大矩阵
print(np.bmat('arr1 arr2;arr1 arr2'))
[[1 2 1 2]
[1 2 1 2]]
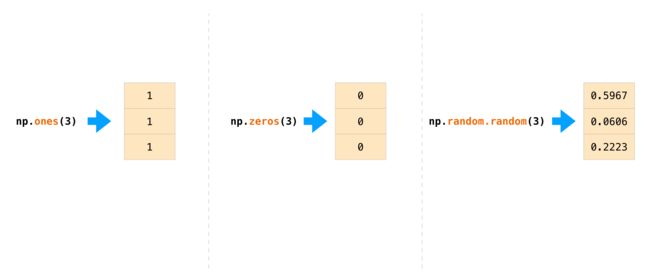
- 特殊矩阵的创建
# 零矩阵 [5,3]表示五行三列
np.zeros([5,3])
array([[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.]])
# 全为1的数组
print(np.ones(3))
# (3,3)表示3*3全为1的矩阵
print('')
print(np.ones((3,3)))
# (2,3,3)表示2个3*3全为1的矩阵构成的矩阵
# print('')
# print(np.ones((2,3,3)),np.ones((2,3,3)).shape)
[1. 1. 1.]
[[1. 1. 1.]
[1. 1. 1.]
[1. 1. 1.]]
# 随机数生成
# random.random生成(0,1)的随机数
print(np.random.random(3))
print(np.random.random((3,3)))
# print(np.random.random((2,3,3)))
[0.85454434 0.47822837 0.90610336]
[[0.48620196 0.05302427 0.17863665]
[0.29284146 0.22803306 0.58954632]
[0.97467534 0.42092292 0.01054189]]
# 指定范围随机整数生成
# np.random.randint(a, b, size=(c, d))
np.random.randint(1,8,size=(2,3))
array([[5, 3, 7],
[4, 7, 6]])
# 二项分布函数np.random.binomial(n,p,size=N)
# n表示实验成功次数,p表示成功概率,size表示实验总次数(2*3)
np.random.binomial(5,0.5,size=(2,3))
array([[2, 2, 3],
[3, 1, 4]])
 |
# 对角阵
list = [1,2,3,4,5]
print(np.diag(list))
a = np.array([1,2,3,4])
print(np.diag(a))
print(np.diag([1,2,3]))
[[1 0 0 0 0]
[0 2 0 0 0]
[0 0 3 0 0]
[0 0 0 4 0]
[0 0 0 0 5]]
[[1 0 0 0]
[0 2 0 0]
[0 0 3 0]
[0 0 0 4]]
[[1 0 0]
[0 2 0]
[0 0 3]]
# 单位矩阵
np.eye(3)
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
更多特殊矩阵参考链接
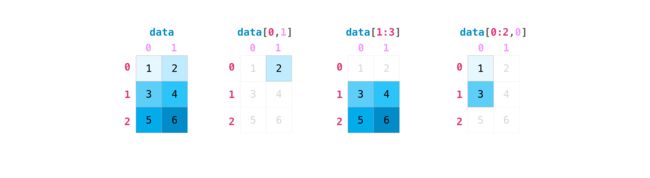
2.3.2 矩阵索引和切片
data = np.array([[1, 2], [3, 4],[5,6]])
#[行范围,列范围],1:3时,取值为左闭右开,即3取不到
print(data[0,1])
print(data[1:3])
print(data[0:2,0])
2
[[3 4]
[5 6]]
[1 3]
 |
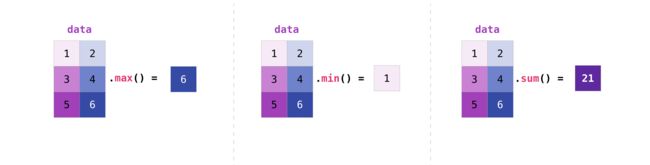
2.3.3 矩阵统计计算
同其余数组求法完全一样,在Pandas中应用极为广泛。
# 求最大值
print(data.max())
# 求最小值
print(data.min())
# 求总和
print(data.sum())
# 求平均值
print(data.mean())
# 求标准差
print(data.std())
6
1
21
3.5
1.707825127659933
 |
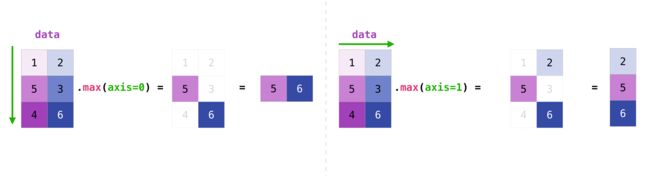
print(data,data.shape)
# 求列最大值
print('\n',data.max(axis=0))
# 求行最大值
print('\n',data.max(axis=1))
[[1 2]
[3 4]
[5 6]] (3, 2)
[5 6]
[2 4 6]
 |
统计其它行或列也是在后面添加坐标轴即可。
- 获取数组唯一值、索引和频数
numpy.unique(ar, return_index=False, return_inverse=False, return_counts=False, axis=None)
a = np.array([11, 11, 12, 13, 14, 15, 16, 17, 12, 13, 11, 14, 18, 19, 20])
# 获取唯一值
print(np.unique(a.reshape(5,3)))
# 获取唯一值、索引
unique_values, indices_list = np.unique(a, return_index=True)
# 获取唯一值、频数
unique_values, occurrence_count = np.unique(a, return_counts=True)
[11 12 13 14 15 16 17 18 19 20]
# 用pandas查看结果
import pandas as pd
df = pd.DataFrame()
df['唯一值'] = unique_values
df['索引'] = indices_list
df['频数'] = occurrence_count
df.head(2)
| 唯一值 | 索引 | 频数 | |
|---|---|---|---|
| 0 | 11 | 0 | 3 |
| 1 | 12 | 2 | 2 |
# 对于二维数组中,即矩阵中也同样适用
a2 = a.reshape(3,5)
print(a2)
print('\n')
# 获取唯一值,未指定axis,结果为一维数组
print(np.unique(a2))
print('\n')
# 指定axis=0,则获取列唯一值
print(np.unique(a2, axis=0))
print('\n')
# 指定axis=1,则获取行唯一值
print(np.unique(a2, axis=1))
[[11 11 12 13 14]
[15 16 17 12 13]
[11 14 18 19 20]]
[11 12 13 14 15 16 17 18 19 20]
[[11 11 12 13 14]
[11 14 18 19 20]
[15 16 17 12 13]]
[[11 11 12 13 14]
[15 16 17 12 13]
[11 14 18 19 20]]
unique_rows, indices, occurrence_count = np.unique(
a2, axis=1, return_counts=True, return_index=True)
print(unique_rows)
print(indices)
print(occurrence_count)
[[11 11 12 13 14]
[15 16 17 12 13]
[11 14 18 19 20]]
[0 1 2 3 4]
[1 1 1 1 1]
2.3.4 矩阵的变换和重塑
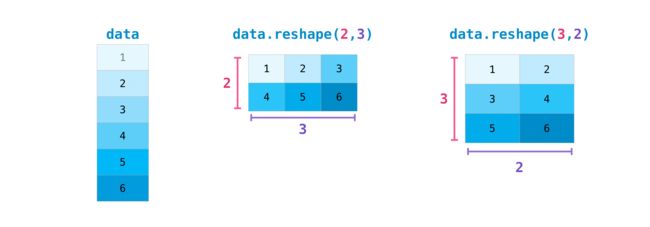
- 矩阵的变换
list = [1,2,3,4,5,6]
data = np.array(list)
data.reshape(2, 3)
array([[1, 2, 3],
[4, 5, 6]])
data.reshape(3, 2)
array([[1, 2],
[3, 4],
[5, 6]])
 |
- 反转数组【np.flip()】
arr = np.array([1, 2, 3, 4, 5, 6, 7, 8])
np.flip(arr)
array([8, 7, 6, 5, 4, 3, 2, 1])
arr_2 = arr.reshape(2,4)
print(arr_2)
print('******')
# 整体反转
print(np.flip(arr_2))
print('******')
# 列反转
print(np.flip(arr_2,axis=0))
print('******')
# 行反转
print(np.flip(arr_2,axis=1))
[[1 2 3 4]
[5 6 7 8]]
******
[[8 7 6 5]
[4 3 2 1]]
******
[[5 6 7 8]
[1 2 3 4]]
******
[[4 3 2 1]
[8 7 6 5]]
# 反转第2行
arr_22 = arr_2.copy()
arr_2[1] = np.flip(arr_2[1])
print(arr_2)
# 反转第2列
arr_22[:,1] = np.flip(arr_2[:,1])
print(arr_22)
[[1 2 3 4]
[8 7 6 5]]
[[1 7 3 4]
[5 2 7 8]]
- 多维数组的整形和平坦化,与reshape作用相反
x = np.array([[1 , 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
# flatten将数组夷为平地为一维数组,对新数组的更改不会更改父数组
a1 = x.flatten()
a1[0] = 100
print(x,'\n',a1)
[[ 1 2 3 4]
[ 5 6 7 8]
[ 9 10 11 12]]
[100 2 3 4 5 6 7 8 9 10 11 12]
# 用ravel,对新数组所做的更改将影响父数组。
a2 = x.ravel()
a2[0] = 100
print(x,'\n',a2)
[[100 2 3 4]
[ 5 6 7 8]
[ 9 10 11 12]]
[100 2 3 4 5 6 7 8 9 10 11 12]
2.3.5 矩阵的相关计算
- 向量的外积与內积
import numpy as np
u = np.array([3,5,2])
v = np.array([1,4,7])
# 內积
print(np.inner(u,v))
# 外积
print(np.outer(u,v))
37
[[ 3 12 21]
[ 5 20 35]
[ 2 8 14]]
import numpy as np
u = np.array([[3,5,2]])
v = np.array([[1,4,7]])
# 內积
print(np.inner(u,v))
# 外积
print(np.outer(u,v))
[[37]]
[[ 3 12 21]
[ 5 20 35]
[ 2 8 14]]
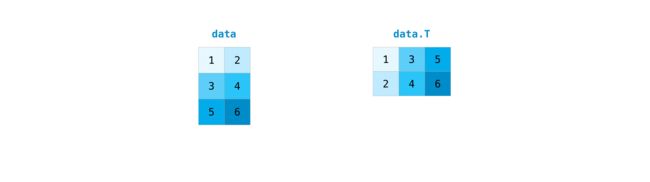
- 矩阵的转置
data = np.array([[1, 2, 3],
[4, 5, 6]])
print(data,'\n\n',data.T)
# 或者用transpose()
print('\n',data.transpose())
[[1 2 3]
[4 5 6]]
[[1 4]
[2 5]
[3 6]]
[[1 4]
[2 5]
[3 6]]
 |
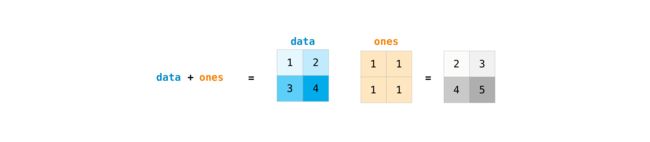
- 矩阵加法运算
两个形状完全一样的才可正确的进行矩阵的加运算
data = np.array([[1, 2], [3, 4]])
ones = np.array([[1, 1], [1, 1]])
data + ones
array([[2, 3],
[4, 5]])
 |
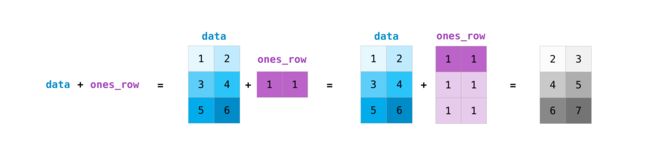
两个形状不一样时的则使用广播规则进行计算
data = np.array([[1, 2], [3, 4], [5, 6]])
ones_row = np.array([[1, 1]])
data + ones_row
array([[2, 3],
[4, 5],
[6, 7]])
 |
- 矩阵乘法运算
矩阵数乘计算
a = np.array([[1,2],
[3,4],
[5,6]])
a * 2
array([[ 2, 4],
[ 6, 8],
[10, 12]])
矩阵与矩阵的乘法(必须满足此关系才可计算【(A,B)*(B,C),A与C可以相等】)
np.dot(a,a.T)
array([[ 5, 11, 17],
[11, 25, 39],
[17, 39, 61]])
矩阵与向量乘法(改变向量的空间位置)
a = np.array([[1,2],
[3,4],
[5,6]])
b = np.array([[1,2]]).T
print(a.shape,b.shape)
np.dot(a,b)
(3, 2) (2, 1)
array([[ 5],
[11],
[17]])
- 矩阵的秩
a = np.array([[1,2],
[3,4],
[5,6]])
np.linalg.matrix_rank(a)
2
- 矩阵的逆(只有方阵才会有逆矩阵)
需要借助Python的另一工具库SciPy计算
import numpy as np
from scipy import linalg
a = np.array([[1,35,0],
[0,2,3],
[0,0,4]])
print(linalg.inv(a))
# 检验,我们知道逆矩阵与原矩阵的乘为单位阵
print(np.dot(a,linalg.inv(a)))
[[ 1. -17.5 13.125]
[ 0. 0.5 -0.375]
[ 0. 0. 0.25 ]]
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]
奇异阵(不可逆矩阵),存在列向量线性相关,即不可逆
b = np.array([[1,0,2],
[0,1,3],
[1,1,5]])
linalg.inv(b)
三、保存与加载NumPy
- 保存
a = np.array([1, 2, 3, 4, 5, 6])
# 默认保存.npy文件
np.save('NP1', a)
np.savetxt('NP2.csv',a)
- 加载(导入)
b = np.load('NP1.npy')
c = np.loadtxt('NP2.csv')
print(b,'\n',c)
[1 2 3 4 5 6]
[1. 2. 3. 4. 5. 6.]
更多保存与加载方法链接