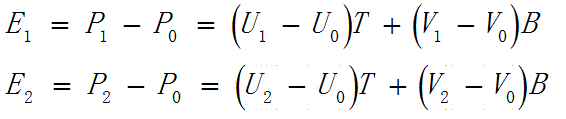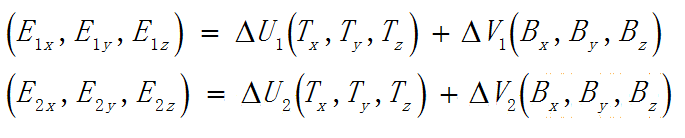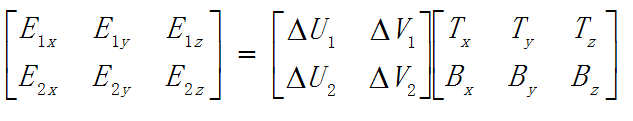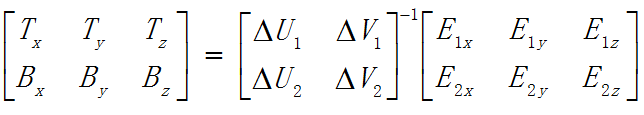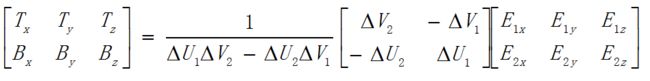本文主要解决一个问题:
如何使用法线贴图给物体添加更多的细节?
引言
学了这么多技巧,也能显示非常酷炫的画面,是不是觉得自己已经非常强,有点飘飘然了?哈哈,还差的远呢。不信?来看下面一张对比图就知道了:
左图明显比右图感觉更真实,细节更多,更带感。你也许会这样想:这两张纹理贴图不一样,这是美术的事情。那你可就错了,这两张图用的是同一张纹理。当然也不是左边的模型更加精细,因为我找不到这么精细的模型,而且自己也不会做。那么,为什么两张图的差距这么大呢?
答案是:左边的场景在渲染时用了法线贴图。
酷不酷,赞不赞, 想不想学?别急,我们慢慢来。
法线贴图
原理
法线贴图,顾名思义,就是将每一个片元(像素)的法线值保存成一张图片。法向量的xyz坐标对应到图的rgb值。这样会产生了一个问题,就是我们的法线xyz的取值范围是[-1,1],而rgb值的取值范围[0,1],我们该怎么样把xyz值转换成rgb值呢?其实,这也很简单,只要将xyz值加1,然后除以2就可以了。翻译成方程式就是:rgb = (xyz + 1) / 2。下面我们就来看看法线贴图长什么样:
怎么蓝不拉叽的?别急,这个问题会在下面解答。
解决了转换成rgb值的问题,我们还有一个非常重要的问题要解决。思考一下,物体的法线在世界空间的不同位置是不同的,我们如何才能用一张图来表示物体的法线,使它能够在所有的情况下都适用呢?仔细想想,法线贴图是贴在物体表面的,我在一个固定的坐标系中生成法线贴图,再通过一个转换矩阵将法线转换到世界空间中,这不就行了吗?
思路没错,关键是如何计算出这个转换矩阵。首先介绍一下,我们生成法线贴图的坐标系称作TBN坐标系,坐标系的三个轴是t轴,b轴和n轴,对应我们熟悉的x轴,y轴和z轴。之所以把这个坐标系称为TBN坐标系,是因为n轴表示的是图元三角形表面法向量。有了法向量之后,我们还需要两个轴来确定这个坐标系。这两个轴是切线轴(tangent )和副切线轴(bitangent ),这三个轴一起组成的坐标系就是TBN坐标系。理论上,T轴可以是图元平面上的任意轴,B轴只需要垂直T轴和N轴就可以了。但是,TBN坐标系不是随随便便弄出来玩的,它的存在价值就是简化计算法向量的步骤。所以,我们通常采用的是和表面纹理坐标一致的轴作为T轴和B轴,即U轴对应T轴,V轴对应B轴,这样,我们就可以用UV值来计算转换矩阵了。
注意TBN坐标系的存在意义就是简化计算变换矩阵的,所以我们的TBN轴就必须按照约定俗成的规范来
上图是法线贴图在TBN坐标系中的状态。
接下来,我们就要来计算在模型空间中的向量T和向量B了。来看下面一张原理图,我们从这张原理图上推导出计算的公式:
假设我们的向量T和B都是单位向量,根据向量共面定理,我们可以列出一个方程式:
介绍一下向量共面定理。
如果e1和e2是同一个平面内两个不共线向量,那么对于平面内的任一向量a,有且只有一对实数(x,y)使得a = x*e1 + y * e2。
在这里,我们的T和B是互相垂直的向量,满足不共线前提,E1和E2也是在TB平面内,其平面坐标我们也知道,所以可以列出上面的等式,这是最重要的一个等式。
在模型空间中,我们可以把这个等式转换成下面的形式:
其中,(delta)U1表示(U1-U0),(delta)V1表示(V1-V0)依次类推。这样我们就非常容易地将这个等式转换成矩阵的形式:
要计算TB的值,我们只需要在等式两边乘以UV矩阵的逆矩阵就行了:
逆矩阵的计算方法我们不用去考究,直接使用下面的最终计算方程式就行:
有了这个方程式,我们就可以计算转换矩阵了。
讲点小历史知识:
在以前,法线贴图需要用高精度模型通过特定的算法计算出来,非常的不方便。后来改进之后才有了我们现在的贴图与模型分离的方法。应用上,PS2不支持法线贴图,XBox360以及之后的主机都支持法线贴图,这已经成为了一种标配。
为什么是蓝兮兮的?
你肯定已经在这个这问题上纠结了很久,为什么法线贴图是这样蓝兮兮的?是不是所有的法线贴图都这样,还是只有这张是这样?
这里我可以负责任地告诉你,所有的法线贴图都是这样蓝兮兮的。原因很好理解,因为我们贴图保存的是切线空间中的法向量值。在切线空间中,法向量的n坐标始终指向+n的方向,它的值就在[0,1]范围内,而t坐标和b坐标的范围是[-1,1]。这样,将tbn三个坐标值映射到贴图的rgb值(通常范围是[0,255])时,贴图中的blue分量就会比较大,从而造成了整张图看上去蓝兮兮的效果。
优缺点
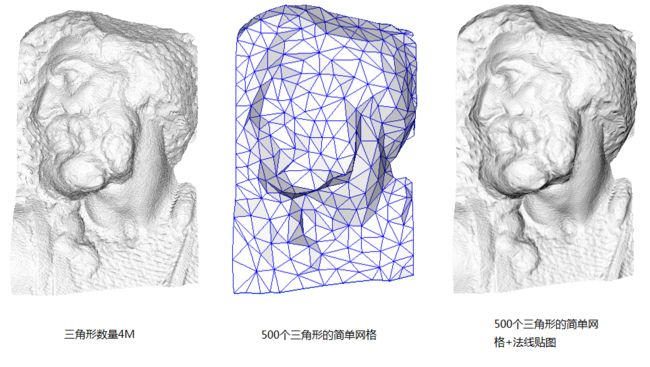
法线贴图的优点,是我们可以用一个低精度模型表现出非常高的细节,看起来像高精度模型那样。来看下面这张图:
只需要500个三角形的简单网格加上法线贴图就能有媲美4M个三角形的精细网格模型的效果,不得不说法线贴图的优势巨大,处理4M个三角形可不是500个三角形那么简单的事情。
当然法线贴图也不是万能的,它也有它的缺点。因为它只是改变了物体表面的光照计算方式,所以它不适合用在凹凸起伏较大的物体上,这些物体会有遮挡的效果,这是法线贴图无法实现的。另外,使用法线贴图的物体经不起特写放大操作,如果摄像机离的很近,或者摄像机的角度刁钻,很容易就会穿帮。
实现
理解原理后,自然就到了实现的过程。基本上,我们最容易想到的方法有两种:
其一、将法线通过TBN矩阵变换后,在世界坐标空间中计算光照效果。
其二、将光源、视点、片元的位置经过TBN矩阵的逆矩阵变换后,在TBN空间中计算光照效果。
两种方法都可行,我们都会进行尝试。不过要先来看看如何计算T和B向量。
要计算T和B向量,我们首先要知道三角形的顶点坐标和纹理坐标。如果我们要显示上面的那一面砖墙,我们就需要4个顶点坐标和4个纹理坐标,外加一个法向量,先来定义这些数据:
//位置
glm::vec3 pos1(-1.0, 1.0, 0.0);
glm::vec3 pos2(-1.0, -1.0, 0.0);
glm::vec3 pos3(1.0, -1.0, 0.0);
glm::vec3 pos4(1.0, 1.0, 0.0);
//纹理坐标
glm::vec2 uv1(0.0, 1.0);
glm::vec2 uv2(0.0, 0.0);
glm::vec2 uv3(1.0, 0.0);
glm::vec2 uv4(1.0, 1.0);
//法向量
glm::vec3 nm(0.0, 0.0, 1.0);
接着,观察公式,计算公式中要用到的数据,这些数据包括E1,E2,deltaU1,deltaV1,deltaU2,deltaV2:
glm::vec3 e1 = pos2 - pos1;
glm::vec3 e2 = pos3 - pos1;
glm::vec2 deltaUV1 = uv2 - uv1;
glm::vec2 deltaUV2 = uv3 - uv1;
然后,计算前面的分数系数,跟着公式走,我们的代码出来了:
float coefficient = 1 / (deltaUV1.x * deltaUV2.y - deltaUV1.y * deltaUV2.x);
最后,计算出T向量和B向量。向量的乘法还记得吗?用前一个矩阵的一行去乘上后一个矩阵的每一列,得到最终矩阵上一行的元素值,以此类推:
glm::vec3 tangent1, bitangent1;
tangent1.x = (deltaUV2.y * e1.x - deltaUV1.y * e2.x) * coefficient;
tangent1.y = (deltaUV2.y * e1.y - deltaUV1.y * e2.y) * coefficient;
tangent1.z = (deltaUV2.y * e1.z - deltaUV1.y * e2.z) * coefficient;
tangent1 = glm::normalize(tangent1);
bitangent1.x = (-deltaUV2.x * e1.x + deltaUV1.x * e2.x) * coefficient;
bitangent1.y = (-deltaUV2.x * e1.y + deltaUV1.x * e2.y) * coefficient;
bitangent1.z = (-deltaUV2.x * e1.z + deltaUV1.x * e2.z) * coefficient;
bitangent1 = glm::normalize(bitangent1);
记得最后要把向量规范化成单位向量。这样,第一个三角形的TB向量就计算好了,第二个三角形就留给读者自己完成吧。
将两个三角形的TB向量都算完之后,我们就可以把这些数据统统放到顶点结构中传递给着色器了:
float quadVertices[] = {
// 位置 // 法线 // 纹理坐标 // 切线 // 副切线
pos1.x, pos1.y, pos1.z, nm.x, nm.y, nm.z, uv1.x, uv1.y, tangent1.x, tangent1.y, tangent1.z, bitangent1.x, bitangent1.y, bitangent1.z,
pos2.x, pos2.y, pos2.z, nm.x, nm.y, nm.z, uv2.x, uv2.y, tangent1.x, tangent1.y, tangent1.z, bitangent1.x, bitangent1.y, bitangent1.z,
pos3.x, pos3.y, pos3.z, nm.x, nm.y, nm.z, uv3.x, uv3.y, tangent1.x, tangent1.y, tangent1.z, bitangent1.x, bitangent1.y, bitangent1.z,
pos1.x, pos1.y, pos1.z, nm.x, nm.y, nm.z, uv1.x, uv1.y, tangent2.x, tangent2.y, tangent2.z, bitangent2.x, bitangent2.y, bitangent2.z,
pos3.x, pos3.y, pos3.z, nm.x, nm.y, nm.z, uv3.x, uv3.y, tangent2.x, tangent2.y, tangent2.z, bitangent2.x, bitangent2.y, bitangent2.z,
pos4.x, pos4.y, pos4.z, nm.x, nm.y, nm.z, uv4.x, uv4.y, tangent2.x, tangent2.y, tangent2.z, bitangent2.x, bitangent2.y, bitangent2.z
};
...
//把T向量和B向量都传递给着色器
glEnableVertexAttribArray(3);
glVertexAttribPointer(3, 3, GL_FLOAT, GL_FALSE, 14 * sizeof(float), (void*)(8 * sizeof(float)));
glEnableVertexAttribArray(4);
glVertexAttribPointer(4, 3, GL_FLOAT, GL_FALSE, 14 * sizeof(float), (void*)(11 * sizeof(float)));
这样,在主流程中的工作就完成了,接下来就是着色器的工作了,我们先来看第一种方法。
方法一:切线空间->世界空间
在顶点着色器中,我们需要把T向量和B向量都接收进来,所以在着色器开头要加上这两行代码:
layout (location = 3) in vec3 aTangent;
layout (location = 4) in vec3 aBitangent;
然后,计算得到的TBN矩阵(就是上面说的转换矩阵)要传递给片元着色器,因此,我们要在输出块中加入一个TBN矩阵作为输出:
out VS_OUT {
vec3 FragPos;
vec2 TexCoords;
mat3 TBN;
} vs_out;
然后计算TBN矩阵:
void main (){
vs_out.TexCoords = aTexCoords;
vs_out.FragPos = vec3(model * vec4(aPos, 1.0));
mat3 normalMatrix = transpose(inverse(mat3(model)));
vec3 T = normalize(normalMatrix * aTangent);
vec3 B = normalize(normalMatrix * aBitangent);
vec3 N = normalize(normalMatrix * aNormal);
vs_out.TBN = mat3 (T,B,N);
gl_Position = projection * view * model * vec4(aPos, 1.0);
}
由于我们的TBN都是模型空间中的坐标,在转换到世界空间中时需要乘上"模型变换矩阵"(这里的变换矩阵当然是要和之前一样的),当然,TBN向量都需要规范化一下才能避免出错。组成TBN矩阵的方式十分简单,直接调用mat3(T,B,N)就行了。
完成顶点着色器的计算后,片元着色器中就能直接使用顶点着色器的计算结果了:
//输入TBN矩阵
in VS_OUT {
vec3 FragPos;
vec2 TexCoords;
mat3 TBN;
} fs_in;
...
void main()
{
// 采样法线贴图
vec3 normal = texture(normalMap, fs_in.TexCoords).rgb;
// 转换法向量到[-1,1]范围
normal = normalize(normal * 2.0 - 1.0); // 此向量是切线空间中的向量
normal = normalize(fs_in.TBN * normal);
// 采样漫反射
vec3 color = texture(diffuseMap, fs_in.TexCoords).rgb;
// 环境光
vec3 ambient = 0.1 * color;
// 漫反射
vec3 lightDir = normalize(lightPos - fs_in.FragPos);
float diff = max(dot(lightDir, normal), 0.0);
vec3 diffuse = diff * color;
// 镜面高光
vec3 viewDir = normalize(viewPos - fs_in.FragPos);
vec3 reflectDir = reflect(-lightDir, normal);
vec3 halfwayDir = normalize(lightDir + viewDir);
float spec = pow(max(dot(normal, halfwayDir), 0.0), 32.0);
vec3 specular = vec3(0.2) * spec;
FragColor = vec4(ambient + diffuse + specular, 1.0);
}
获取法向量的方式和采样颜色值一样,采样完成后,需要将值转换回[-1,1]的区间内,然后,用TBN矩阵乘上法向量再规范化,我们要的世界空间中的法向量就横空出世了。其余的部分是Blinn-Phong光照模型的实现代码,如果你看过我前面的文章,肯定很熟悉这套代码了。
再写一些边边角角的代码,让模型动起来方便我们观察效果。将模型在光源的位置也显示出来,这样我们就能知道光照效果对不对了:
model = glm::rotate(model, currentRadians, glm::normalize(glm::vec3(1.0, 0.0, 1.0))); // 旋转平面观察不同角度的效果
...
//在光源位置显示一个小砖墙
model = glm::mat4();
model = glm::translate(model, lightPos);
model = glm::scale(model, glm::vec3(0.1f));
method1shader.setMat4("model", glm::value_ptr(model));
renderQuad();
好,完成之后我们就可以看看效果了:
8错8错,是我们要的效果。
方法二:世界空间->切线空间
使用这个方法,我们不需要将TBN矩阵传递给片元着色器了,而是要在顶点着色器中,将光源位置、视点位置、片元位置通过TBN矩阵的逆矩阵转换好之后,将转换过后的坐标传递给片元着色器让它使用。
好了,动手!新建一个顶点着色器和片元着色器,取名method2Shader.vs和method2Shader.fs,将方法一中的代码都复制过来,我们在它的基础上-改。首先,去掉VS_OUT块中的TBN矩阵,加入我们计算好的光源、视点和片元位置:
out VS_OUT {
vec3 FragPos;
vec2 TexCoords;
vec3 TangentLightPos;
vec3 TangentViewPos;
vec3 TangentFragPos;
} vs_out;
然后,在代码中,我们计算出的TBN矩阵要进行一下转置计算(这里的矩阵比较特殊,转置操作就是取当前矩阵的逆矩阵),用这个转置矩阵来算出光源、视点和片元的位置。
void main()
{
vs_out.FragPos = vec3(model * vec4(aPos, 1.0));
vs_out.TexCoords = aTexCoords;
mat3 normalMatrix = transpose(inverse(mat3(model)));
vec3 T = normalize(normalMatrix * aTangent);
vec3 N = normalize(normalMatrix * aNormal);
T = normalize(T - dot(T, N) * N);
vec3 B = cross(N, T);
mat3 TBN = transpose(mat3(T, B, N));
vs_out.TangentLightPos = TBN * lightPos;
vs_out.TangentViewPos = TBN * viewPos;
vs_out.TangentFragPos = TBN * vs_out.FragPos;
gl_Position = projection * view * model * vec4(aPos, 1.0);
}
可以看到,我们其实并不需要将T和B向量都传递进来,有了T和N向量之后,我们完全可以通过叉乘来计算出B向量。
在大量的计算过程中,TBN向量可能会变得不两两垂直,这就会导致我们的模型有瑕疵。因此,一种名叫Gram-Schmidt正交化的方法就被创造出来。通过一点很小的代价,让TBN向量继续两两垂直,这样,我们的模型显示就完美无瑕了。上面的代码中,T = normalize(T - dot(T, N) * N);就是正交化过程。
片元着色器中,我们将原本用来接收的结构改成顶点着色器传过来的结构:
in VS_OUT {
vec3 FragPos;
vec2 TexCoords;
vec3 TangentLightPos;
vec3 TangentViewPos;
vec3 TangentFragPos;
} fs_in;
计算光照时,去掉用TBN矩阵转换法向量的过程,只将采样的法向量转换回[-1,1]空间就行了。然后,在计算光照的时候,必须使用从顶点传过来的光源、片元和视点位置,我们的代码就成了这个样子:
void main()
{
// 采样法线贴图
vec3 normal = texture(normalMap, fs_in.TexCoords).rgb;
// 转换法向量到[-1,1]范围
normal = normalize(normal * 2.0 - 1.0); // 此向量是切线空间中的向量
// 采样漫反射
vec3 color = texture(diffuseMap, fs_in.TexCoords).rgb;
// 环境光
vec3 ambient = 0.1 * color;
// 漫反射
vec3 lightDir = normalize(fs_in.TangentLightPos - fs_in.TangentFragPos);
float diff = max(dot(lightDir, normal), 0.0);
vec3 diffuse = diff * color;
// 镜面高光
vec3 viewDir = normalize(fs_in.TangentViewPos - fs_in.TangentFragPos);
vec3 reflectDir = reflect(-lightDir, normal);
vec3 halfwayDir = normalize(lightDir + viewDir);
float spec = pow(max(dot(normal, halfwayDir), 0.0), 32.0);
vec3 specular = vec3(0.2) * spec;
FragColor = vec4(ambient + diffuse + specular, 1.0);
}
再修改一下主函数的代码,编译运行,你看到的结果应该和上面一样。
添加一些控制功能
每次总是运行一个着色器文件,完全没法看出对比效果是不是?不要急,我们这就来添加一些控制的功能。我们想要的功能有两个:1、在方法一、方法二和使用法线贴图的着色器之间切换。2、暂停旋转,方便切换比较。
切换功能
实现切换功能很容易,在全局空间中添加一个渲染类型变量,初始值设置成1,表示方法1
int renderType = 1; //绘制方式:1、不使用法线贴图;2、切线空间->世界空间;3、世界空间->切线空间
然后,在键盘控制的处理函数中,添加如下的处理代码:
if (glfwGetKey(window, GLFW_KEY_1) == GLFW_PRESS)
renderType = 1;
if (glfwGetKey(window, GLFW_KEY_2) == GLFW_PRESS)
renderType = 2;
if (glfwGetKey(window, GLFW_KEY_3) == GLFW_PRESS)
renderType = 3;
当我们按下1的时候,使用方法1的着色器;按下2时,使用方法2着色器;按下3时,使用不进行法线贴图计算的着色器。在渲染循环中,我们也要相应地添加一些设置代码:
if (renderType == 1) {
method1shader.use();
method1shader.setMat4("projection", glm::value_ptr(projection));
method1shader.setMat4("view", glm::value_ptr(view));
}
else if (renderType == 2) {
method2shader.use();
method2shader.setMat4("projection", glm::value_ptr(projection));
method2shader.setMat4("view", glm::value_ptr(view));
}
else {
shaderWithoutNormalMap.use();
shaderWithoutNormalMap.setMat4("projection", glm::value_ptr(projection));
shaderWithoutNormalMap.setMat4("view", glm::value_ptr(view));
}
//还有设置模型坐标,光源位置,视点位置的工作请自行完成。
完成之后,我们就可以在3种方式中之间随意切换了。
暂停功能
暂停功能的实现更加简单。第一步先在全局变量中添加暂停变量以及当前角度变量(用来保存当前旋转到哪个角度):
bool isPause = false; //是否暂停
float currentRadians = 0.0f; //当前旋转角度
紧接着,在处理按钮的地方添加处理。当我们按下z键时,暂停旋转,按下x键时,继续旋转:
if (glfwGetKey(window, GLFW_KEY_Z) == GLFW_PRESS)
isPause = true;
if (glfwGetKey(window, GLFW_KEY_X) == GLFW_PRESS)
isPause = false;
最后,在生成模型矩阵之前,判断是否暂停,如果暂停,就不对当前旋转角度进行刷新:
if (!isPause)
currentRadians = glm::radians((float)glfwGetTime() * -10.0f);
model = glm::rotate(model, currentRadians, glm::normalize(glm::vec3(1.0, 0.0, 1.0))); // 旋转平面观察不同角度的效果
写完这些代码后,编译运行一下,看看是否有效。(当然有效,不然我上面的图是咋截的~)
最后,附上完整的代码以供参考。
讲点题外话
首先我要对那些一直等待我写教程的读者郑重地说一句:对不起,你们久等了!
在跨年的时候,我忽然就有一种不同的觉悟,那就是我想做的是一个有趣有料的opengl教程,而不是单纯的翻译。所以,我放弃了翻译,选择了静下心来多找资料,多尝试,多研究。期间我也经历了一个概念死活搞不懂带来的烦躁和郁闷,那时候想,如果我只是翻译该多好啊,那样我就能写的很快。但是,每当这种想法出现的时候,我就静下心来问问自己,我是想要一篇翻译的东西还是要一个卓越的教程?
经过挣扎,我还是选择了后者,于是便继续死磕。不过,我还只是一个初级图形程序员,要做一个有趣有料的教程并不是我一个人能完成的。在这里,希望看到这里的读者能帮我一个忙,如果你也想把学习的心得记录下来的话,非常欢迎对这教程补充或者指正,感谢大家的理解与支持,谢谢!
总结
本章最重要的知识是法线贴图的原理。通过向量共面定理计算出模型空间中的T向量和B向量。然后生成TBN矩阵,这个矩阵可以将法向量从TBN空间转换到模型空间中,再通过模型变换矩阵转换到世界空间就非常简单了。
下一篇
目录
上一篇
参考资料
www.learnopengl.com
维基百科
应用历史
Tutorial 26: Normal Mapping