matlab---k-means算法、fuzzy-c-means算法详解和比较
k-means算法
(1)k-means算法和fuzzy-c-means算法都是聚类划分法的一种。聚类是把相似的对象通过静态分类的方法分成不同的组别或者更多的子集,这样让在同一个子集中的成员对象都有相似的一些属性
(2)聚类中的划分法:给定一个有N个元组或者纪录的数据集,构造K ( K < N)个分组,每一个分组就代表一个聚类:每一个分组至少包含一个数据纪录且每一个数据纪录属于且仅属于一个分组。对于给定的K,算法首先给出一个初始的分组方法,以后通过反复迭代的方法改变分组,使得每一次改进之后的分组方案都较前一次好,而所谓好的标准就是:同一分组中的记录越近越好,而不同分组中的纪录越远越好
聚类算法可以应用于许多领域,例如:
营销:找到具有相似行为的客户群体,提供包含其属性和过去购买记录的大量客户数据数据库;
生物学:赋予植物和动物特征的分类;
图书馆:书籍订购;
保险:确定平均索赔成本高的汽车保险单位群体; 识别欺诈
城市规划:根据房屋类型,价值和地理位置确定房屋群;
地震研究:聚类观测地震震中识别危险区域;
(3)k-means算法:该算法为硬聚类算法,隶属度只有两个取值0或1,是基于原型的目标函数聚类方法的代表,它是数据点到原型的某种距离作为优化的目标函数,利用函数求极值的方法得到迭代运算的调整规则。K-means算法以欧式距离作为相似度测度,它是求对应某一初始聚类中心向量V最优分类,使得评价指标J最小。算法采用误差平方和准则函数作为聚类准则函数。
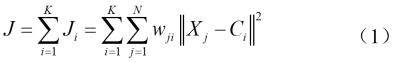
A.k-means的归属矩阵:
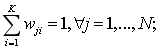
![]()
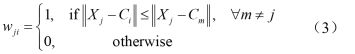

B.k-means实现步骤
(1)随机选取k个数据点Ci,i=1,2,3,…,k 并将之分别视为各聚类的初始中心。
(2)决定各数据点所属之聚类,若数据点X判定属于第i聚类,则权重值wji = 1,否则为0。
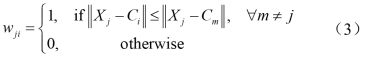
且满足
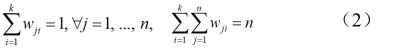
(3)由(1)式计算目标函数 J,如果 J 保持不变,代表聚类结果已经稳定不变,则可结束此迭代方法,否则进入步骤(4)
![]()
(4)以(4)式更新聚类的中心点。回到步骤(2)

C.N次迭代以后

D.算法的优缺点:
优点:算法快速、简单; 对大数据集有较高的效率并且是可伸缩性的;时间复杂度近于线性,而且适合挖掘大规模数据集。K-Means聚类算法的时间复杂度是O(nkt) ,其中n代表数据集中对象的数量,t代表着算法迭代的次数,k代表着簇的数目。
缺点: 在 K-means 算法中 K 是事先给定的,这个 K 值的选定是非常难以估计的,因此事先并不知道给定的数据集应该分成多少个类别才最合适。
在 K-means 算法中,首先需要根据初始聚类中心来确定一个初始划分,然后对初始划分进行优化,若初始值选择的不好,可能无法得到有效的聚类结果。
该算法需要不断地进行样本分类调整,不断地计算调整后的新的聚类中心,因此当数据量非常大时,算法的时间开销是比较非常大的。
设计步骤
使用该算发需事先确定聚类的数目k,若初始聚类中心位置不理想,使得目标函数 J 落入局部解,最后分类出来的群集将不理想
(1)设定聚类数目K,最大执行步骤tmax,一个很小的容忍误差ε>0
(2)决定聚类中心起始位置Cj(0),0 < j ≤ K
(3) for t=1,…,tmax
(A)for j=1,…,N
i计算各数据点到聚类中心的距离
![]()
ii计算数据点属于哪一聚类(隶属度矩阵)

(B)更新聚类中心
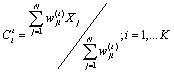
(C)计算收敛准则,若
![]()
![]()
成立则停止运算,否则进行下一轮迭代
使用k-means算法前后对比:
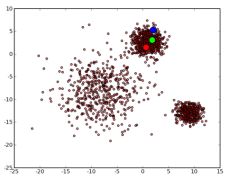
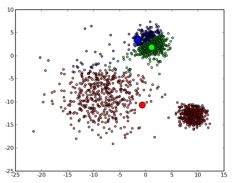
K-Means算法聚类是一种“硬划分”,它把每个待辨识的对象严格地划分到某个类中,具有非此即彼的性质。
例子
这两个方法都是迭代求取最终的聚类划分,即聚类中心与隶属度值。两者都不能保证找到问题的最优解,都有可能收敛到局部极值,模糊c均值甚至可能是鞍点。
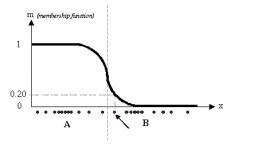
eg:一个一维的例子来说,给定一个特定数据集,分布如下图
![]()
k-means: 图中有两类数据,为A和B,利用k-means 算法,每个数据关联一个特定的质心,隶属度函数如下所示:
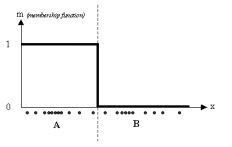
详细设计
clear all;close all;clc;
% µÚÒ»×éÊý¾Ý
mu1=[0 0 ]; %¾ùÖµ
S1=[.1 0 ;0 .1]; %з½²î
data1=mvnrnd(mu1,S1,100); %²úÉú¸ß˹·Ö²¼Êý¾Ý
%µÚ¶þ×éÊý¾Ý
mu2=[1.25 1.25 ];
S2=[.1 0 ;0 .1];
data2=mvnrnd(mu2,S2,100);
% µÚÈý×éÊý¾Ý
mu3=[-1.25 1.25 ];
S3=[.1 0 ;0 .1];
data3=mvnrnd(mu3,S3,100);
% ÏÔʾÊý¾Ý
plot(data1(:,1),data1(:,2),'b+');
hold on;
plot(data2(:,1),data2(:,2),'r+');
plot(data3(:,1),data3(:,2),'g+');
grid on;
% ÈýÀàÊý¾ÝºÏ³ÉÒ»¸ö²»´ø±êºÅµÄÊý¾ÝÀà
data=[data1;data2;data3];
N=3;%ÉèÖþÛÀàÊýÄ¿
[m,n]=size(data);
pattern=zeros(m,n+1);
center=zeros(N,n);%³õʼ»¯¾ÛÀàÖÐÐÄ
pattern(:,1:n)=data(:,:);
for x=1:N
center(x,:)=data( randi(300,1),:);%µÚÒ»´ÎËæ»ú²úÉú¾ÛÀàÖÐÐÄ
end
while 1
distence=zeros(1,N);
num=zeros(1,N);
new_center=zeros(N,n);
for x=1:m
for y=1:N
distence(y)=norm(data(x,:)-center(y,:));%¼ÆË㵽ÿ¸öÀàµÄ¾àÀë
end
[~, temp]=min(distence);%Çó×îСµÄ¾àÀë
pattern(x,n+1)=temp;
end
k=0;
for y=1:N
for x=1:m
if pattern(x,n+1)==y
new_center(y,:)=new_center(y,:)+pattern(x,1:n);
num(y)=num(y)+1;
end
end
new_center(y,:)=new_center(y,:)/num(y);
if norm(new_center(y,:)-center(y,:))<0.1
k=k+1;
end
end
if k==N
break;
else
center=new_center;
end
end
[m, n]=size(pattern);
%×îºóÏÔʾ¾ÛÀàºóµÄÊý¾Ý
figure;
hold on;
for i=1:m
if pattern(i,n)==1
plot(pattern(i,1),pattern(i,2),'r*');
plot(center(1,1),center(1,2),'ko');
elseif pattern(i,n)==2
plot(pattern(i,1),pattern(i,2),'g*');
plot(center(2,1),center(2,2),'ko');
elseif pattern(i,n)==3
plot(pattern(i,1),pattern(i,2),'b*');
plot(center(3,1),center(3,2),'ko');
elseif pattern(i,n)==4
plot(pattern(i,1),pattern(i,2),'y*');
plot(center(4,1),center(4,2),'ko');
else
plot(pattern(i,1),pattern(i,2),'m*');
plot(center(4,1),center(4,2),'ko');
end
end
grid on;
实验结果
初始数据:

N=3时

N=4
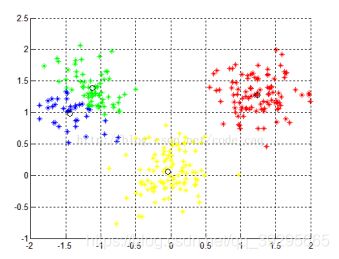
N=5

结果分析
在测试k-means算法时,出现了两类点重叠,经过分析我认为时因为该算法不适合处理离散型数据,但是对于连续型具有较好的聚类效果。对于不同的初始值,可能会导致不同结果,多设置一些不同的初值,但比较耗时和浪费资源。
该算法得出的结果并不稳定,原因就是该算法对初始质心选取很敏感,随机选取质心可能会得到错误结果并且迭代次数也会变大,若初始质心刚好分别处于5个簇之中,那么算法结果就会稳定了。初始质心的距离不应太近,因此可做以下优化:
1.从输入的数据点集合中随机选择一个点作为第一个聚类中心
2.对于数据集中的每一个点,计算它与已选择的聚类中心中最近聚类中心的距离D(x)
3.选择一个新的数据点作为新的聚类中心,选择的原则是D(x)较大的点,
被选取作为聚类中心的概率较大
4.重复2和3直到选择出k个聚类质心
5.利用这k个质心来作为初始化质心去运行标准的K-Means算法
fuzzy-c-means算法
一种模糊聚类算法,是k-means聚类算法的推广形式,隶属度取值为[0 1]区间内的任何一个数,提出的基本根据是“类内加权误差平方和最小化”准则;其目标函数定义如同K-Means聚类法,但其权重矩阵 W 不再是二元矩阵,而是应用了模糊理论的概念,使得每一输入向量不再仅归属于某一特定的聚类,而以其归属程度来表现属于各聚类的程度
![]()
A.fuzzy-c-means算法实现步骤:
(1)设定分类个数 k,设定初始权重矩阵,随机给定 0~1 之值,并满足权重总和为1 ,如下式
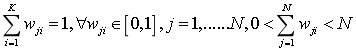
(2)计算聚类中心点

(3)由目标函数式计算目标函数值,当目标函数值小于设定的容忍误差可结束迭代过程,否则执行
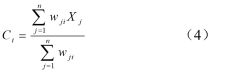
(4)重新计算权重矩阵W,并回到步骤B进行运算
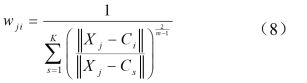
B.算法的优缺点:
Fuzzy-c-means算法是基于对目标函数的优化基础上的一种数据聚类方法。该算法是一种无监督的模糊聚类方法,在算法实现过程中不需要人为的干预。这种算法的不足之处:首先算法中需要设定一些参数,若参数的初始化选取的不合适,可能影响聚类结果的正确性;其次,当数据样本集合较大并且特征数目较多时,算法的实时性不太好,另外该算法容易陷入局部最小,对初始值敏感
设计步骤
同样地需事先确定聚类的数目,与K-Means的差异在于Fuzzy C-Means聚类法加入了模糊的概念,使得每一输入向量不再仅隶属于某一特定的聚类,而是以其隶属程度来表现
(1)设定聚类数目K,最大执行步骤tmax,一个很小的容忍误差ε>0
(2) 决定聚类中心起始位置Cj(0),0 < j ≤ K
(3)for t=1,…, tmax
A. for j=1,…,N ,计算隶属度矩阵

B. for i=1,…,K,更新聚类中心点.

C. 计算收敛准则,若下列等式成立则停止运算,否则进行下一轮迭代
![]()
![]()
例子
fuzzy c-means:同一个数据并不单独属于一个分类,而是可以出现在中间。在这个例子中,隶属函数变得更加平滑,表明每个数据可能属于几个分类。
详细设计
function [U,P,Dist,Cluster_Res,Obj_Fcn,iter]=fuzzycm(Data,C,plotflag,M,epsm)
% 模糊 C 均值聚类 FCM: 从随机初始化划分矩阵开始迭代
% [U,P,Dist,Cluster_Res,Obj_Fcn,iter] = fuzzycm(Data,C,plotflag,M,epsm)
% 输入:
% Data: N×S 型矩阵,聚类的原始数据,即一组有限的观测样本集,
% Data 的每一行为一个观测样本的特征矢量,S 为特征矢量
% 的维数,N 为样本点的个数
% C: 聚类数,1
% plotflag: 聚类结果 2D/3D 绘图标记,0 表示不绘图,为缺省值
% M: 加权指数,缺省值为 2
% epsm: FCM 算法的迭代停止阈值,缺省值为 1.0e-6
% 输出:
% U: C×N 型矩阵,FCM 的划分矩阵
% P: C×S 型矩阵,FCM 的聚类中心,每一行对应一个聚类原型
% Dist: C×N 型矩阵,FCM 各聚类中心到各样本点的距离,聚类中
% 心 i 到样本点 j 的距离为 Dist(i,j)
% Cluster_Res: 聚类结果,共 C 行,每一行对应一类
% Obj_Fcn: 目标函数值
% iter: FCM 算法迭代次数
% See also: fuzzydist maxrowf fcmplot
if nargin<5
epsm=1.0e-6;
end
if nargin<4
M=2;
end
if nargin<3
plotflag=0;
end
[N,S]=size(Data);m=2/(M-1);iter=10000;
Dist(C,N)=0; U(C,N)=0; P(C,S)=0;
% 随机初始化划分矩阵
U0 = rand(C,N);
U0=U0./(ones(C,1)*sum(U0));
% FCM 的迭代算法
while true
% 迭代计数器
iter=iter+1;
% 计算或更新聚类中心 P
Um=U0.^M;
P=Um*Data./(ones(S,1)*sum(Um'))';
% 更新划分矩阵 U
for i=1:C
for j=1:N
Dist(i,j)=fuzzydist(P(i,:),Data(j,:));
end
end
U=1./(Dist.^m.*(ones(C,1)*sum(Dist.^(-m))));
% 目标函数值: 类内加权平方误差和
if nargout>4 | plotflag
Obj_Fcn(iter)=sum(sum(Um.*Dist.^2));
end
% FCM 算法迭代停止条件
if norm(U-U0,Inf) break
end
U0=U;
end
% 聚类结果
if nargout > 3
res = maxrowf(U);
for c = 1:
v = find(res==c);
Cluster_Res(c,1:length(v))=v;
end
end
% 绘图
if plotflag
fcmplot(Data,U,P,Obj_Fcn);
end
实验结果
N=3
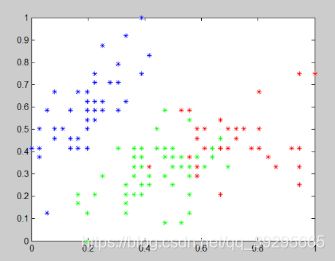
N=4
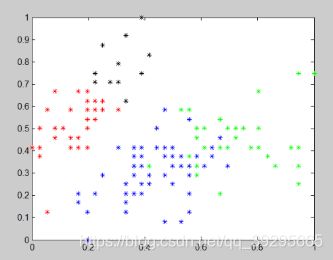
模糊聚类属于识别模式中的无监督学习,不需要训练样本,可以直接通过机器学习达到自动分类的目的。fuzzy c-means算法的隶属度为0-1中间的任意数,反映了数据点和类中心的实际关系。由程序运行的结果可以看出,在两种不同的距离参数下对点的聚类中心质点是不同的根据生成的图可以观察到聚类所分成的三类在点的数量上有细微的差别。