【机器学习(11)】决策树模型:CART分类及回归树可视化
1. 决策树模型
1) 概念: 基于树形结构来拟合自变量与因变量之间的关系
2) 划分算法: 选择最佳划分特征及特征中最佳划分点位置的算法(三大类别)
ID3: 信息增益判断;
C4.5: 信息增益率判断;
CART: GINI系数判断
3) CART基尼系数法算法流程:
①迭代计算每个特征的每个二分切点gini系数
②选取gini最小的特征及对应切分点为最佳分裂点
③进行一次样本划分
④对划分后的两部分样本重复上述迭代过程,逐步向下分裂
⑤所有样本被分到叶节点中
⑥结束
4) 树模型是否越分叉越多,结构越复杂越好?
一般树分叉越多,结构越复杂,在训练集上表现其实会越好的,但是为了防止过拟合,树的分支和深度往往需要被限制的,这也就产生了剪枝策略(有点类似大学运筹中的分支定界法)
5) 剪枝策略
目的:降低模型复杂度,防止过拟合
预剪枝:在构建树的过程中,先计算当前的分裂是否能带来模型泛化能力的提升,如果不能,则不继续生长
后剪枝:让算法生成一颗完整的决策树之后,然后从最底层向上计算,如果对分裂点剪枝,模型的泛化能力提升,则进行剪枝
2. 代码实现
2.1 加载数据和定义类型标签及划分数据集
这一部在之前的操作中已经多次重复了,这里可以直接输出
import pandas as pd
import matplotlib.pyplot as plt
import os
os.chdir(r'C:\Users\86177\Desktop')
# 样例数据读取
df = pd.read_excel('realestate_sample_preprocessed.xlsx')
# 根据共线性矩阵,保留与房价相关性最高的日间人口,将夜间人口和20-39岁夜间人口进行比例处理
def age_percent(row):
if row['nightpop'] == 0:
return 0
else:
return row['night20-39']/row['nightpop']
df['per_a20_39'] = df.apply(age_percent,axis=1)
df = df.drop(columns=['nightpop','night20-39'])
# 制作标签变量
price_median = df['average_price'].median()
df['is_high'] = df['average_price'].map(lambda x: True if x>= price_median else False)
print(df['is_high'].value_counts())
# 数据集基本情况查看
print(df.shape)
print(df.dtypes)
# 划分数据集
x = df[['complete_year','area', 'daypop', 'sub_kde',
'bus_kde', 'kind_kde','per_a20_39']]
y = df['is_high']
print(x.shape)
print(y.shape)
–> 输出的结果为:
True 449
False 449
Name: is_high, dtype: int64
(898, 10)
id int64
complete_year int64
average_price float64
area float64
daypop float64
sub_kde float64
bus_kde float64
kind_kde float64
per_a20_39 float64
is_high bool
dtype: object
(898, 7)
(898,)
2.2 构建决策树模型
由于选取的是类型标签不是数值标签,这里导入的是决策树分类器,如果要进行决策树回归的话就导入下面注释的语句代码
from sklearn.tree import DecisionTreeClassifier
# 如果是回归问题,就要引入回归模型
#from sklearn.tree import DecisionTreeRegressor
# 建立模型
clf_tree = DecisionTreeClassifier(criterion='gini',
splitter='best',
max_depth=3,
min_samples_split=2,
min_samples_leaf=5,
max_features=None,
max_leaf_nodes=10,
min_impurity_decrease=0.0,
min_impurity_split=None,
class_weight=None)
# 训练决策树模型
clf_tree.fit(x,y)
print(clf_tree)
–> 输出的结果为:
DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=3,
max_features=None, max_leaf_nodes=10,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=5, min_samples_split=2,
min_weight_fraction_leaf=0.0, presort=False,
random_state=None, splitter='best')
2.3 决策树参数讲解
criterion:划分算法 默认是gini,另外一种是entropy就是信息增益, 回归模型可以选择mse或mae
splitter:两个选择,best(中小型数据)或者random(大数据)。
max_features:控制所搜的特征数量(一般是默认,如果建模数据量过大,建议调整一下这个参数)
max_depth: 控制树的深度(控制过拟合的重要参数,过拟合限制,欠拟合就增加深度)
min_samples_split: 任意节点样本量达到多少的时候就不再分裂(推荐默认值,也是控制过拟合的,适用大数据)
min_samples_leaf:每一个叶子上最少的样本数(控制最后一个叶节点的样本量,一般提高这个值可以防止过拟合)
max_leaf_nodes:最大叶节点数量(切分数据集的最大的叶节点的数量,有个上界)
min_impurity_decrease: 切分点不纯度最小减少程度(后剪枝的控制参数)
min_impurity_split: 切分点最小不纯度(预剪枝的控制参数)
class_weight:指定样本各类别的的权重(分类模型特有的,防止某个样本的权重过大,导致决策树过于偏向这个样本特征)
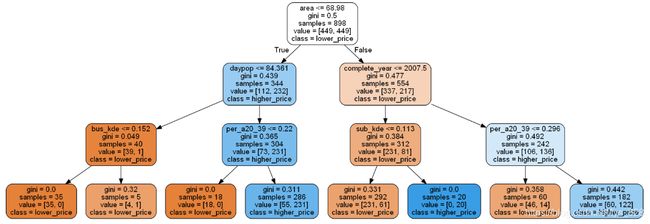
3. 运行结果可视化
import graphviz
import os
os.environ["PATH"] += os.pathsep + r'D:\Anaconda\graphviz-2.38\release\bin'
from IPython.display import Image
import pydotplus
features = ['complete_year','area', 'daypop', 'sub_kde',
'bus_kde', 'kind_kde','per_a20_39']
classes=['lower_price','higher_price']
# 定义图像
from sklearn import tree
tree_graph_data = tree.export_graphviz(clf_tree,
feature_names=features,
class_names=classes,
filled=True,
rounded=True)
# 绘图:
tree_graph = pydotplus.graph_from_dot_data(tree_graph_data)
Image(tree_graph.create_png())