LeetCode刷题1:第八周
LeetCode刷题1:第八周
目录
- LeetCode刷题1:第八周
-
- 前言
- 一、知识点
-
- 1.1 基本思想:
- 1.2 一般步骤:
- 1.3 子集树模板
- 1.4排列树模板
- 二、LeetCode例题
-
- 1688. 比赛中的配对次数
- 46. 全排列
- 77. 组合
- 131. 分割回文串
- 22. 括号生成
相关系列笔记:
LeetCode刷题:前言
LeetCode刷题1:第一周
LeetCode刷题1:第二周
LeetCode刷题1:第三周
LeetCode刷题1:第四周
LeetCode刷题1:第五周
LeetCode刷题1:第六周
LeetCode刷题1:第七周
LeetCode刷题1:第八周
前言
【week 8】Topic:回溯法
(1)1688.比赛中的配对次数
(2)46.全排列
(3)77.组合
(4)131.分割回文串
(5)22.括号生成
一、知识点
在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。
也叫试探法,它是一种系统地搜索问题的解的方法。
1.1 基本思想:
从一条路往前走,能进则进,不能进则退回来,换一条路再试。
1.2 一般步骤:
• 定义一个解空间(子集树、排列树二选一)
• 利用适于搜索的方法组织解空间。
• 利用深度优先法搜索解空间。
• 利用剪枝函数避免移动到不可能产生解的子空间。
1.3 子集树模板
遍历子集树,时间复杂度 O(2^n)
如果解的长度是不固定的,那么解和元素顺序无关,即可以从中选择0个或多个。例如:子集,迷宫,…
如果解的长度是固定的,那么解和元素顺序有关,即每个元素有一个对应的状态。例如:子集,8皇后,…
解空间的个数指数级别的,为2^n,可以用子集树来表示所有的解
适用于:幂集、子集和、0-1背包、装载、8皇后、迷宫、…
1.4排列树模板
遍历排列树,时间复杂度O(n!)
解空间是由n个元素的排列形成,也就是说n个元素的每一个排列都是解空间中的一个元素,那么,最后解空间的组织形式是排列树
适用于:n个元素全排列、旅行商、…
二、LeetCode例题
1688. 比赛中的配对次数
给你一个整数 n ,表示比赛中的队伍数。比赛遵循一种独特的赛制:
• 如果当前队伍数是 偶数 ,那么每支队伍都会与另一支队伍配对。总共进行 n / 2 场比赛,且产生 n / 2 支队伍进入下一轮。
• 如果当前队伍数为 奇数 ,那么将会随机轮空并晋级一支队伍,其余的队伍配对。总共进行 (n - 1) / 2 场比赛,且产生 (n - 1) / 2 + 1 支队伍进入下一轮。
返回在比赛中进行的配对次数,直到决出获胜队伍为止。
示例 1:
输入:n = 7
输出:6
解释:比赛详情:
- 第 1 轮:队伍数 = 7 ,配对次数 = 3 ,4 支队伍晋级。
- 第 2 轮:队伍数 = 4 ,配对次数 = 2 ,2 支队伍晋级。
- 第 3 轮:队伍数 = 2 ,配对次数 = 1 ,决出 1 支获胜队伍。
总配对次数 = 3 + 2 + 1 = 6
示例 2:
输入:n = 14
输出:13
解释:比赛详情:
- 第 1 轮:队伍数 = 14 ,配对次数 = 7 ,7 支队伍晋级。
- 第 2 轮:队伍数 = 7 ,配对次数 = 3 ,4 支队伍晋级。
- 第 3 轮:队伍数 = 4 ,配对次数 = 2 ,2 支队伍晋级。
- 第 4 轮:队伍数 = 2 ,配对次数 = 1 ,决出 1 支获胜队伍。
总配对次数 = 7 + 3 + 2 + 1 = 13
提示:
• 1 <= n <= 200
class Solution:
def numberOfMatches(self, n: int) -> int:
# a 比赛的场数
# 分情况讨论:n 是偶数或者奇数
a = 0
while n > 1:
if n % 2 == 0:
a += n / 2
n = n / 2
else:
a += (n - 1) / 2
n = (n - 1) / 2 + 1
return int(a)
46. 全排列
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
示例:
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
# 将第index位的数字与数组中后半段[index+1 : length]的数字依次交换
# 完成交换后,则递归调用helper()函数,完成后续的数组中[index+1 : length]的交换
# 当发现index等于数组长度,说明已经完成数组中所有数字的交换,输出结果
res, length = [], len(nums)
def helper(index):
if index == length:
res.append(list(nums))
for i in range(index, length):
nums[index], nums[i] = nums[i], nums[index]
helper(index+1)
nums[index], nums[i] = nums[i], nums[index]
helper(0)
return res
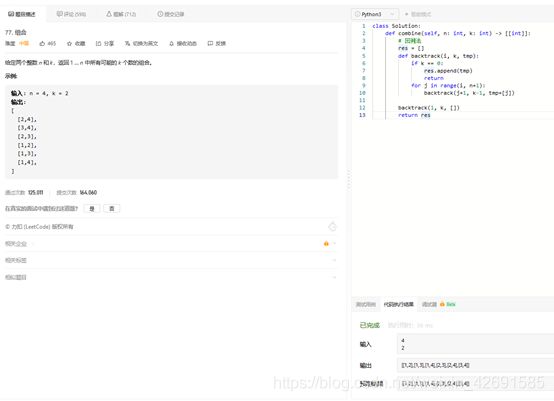
77. 组合
给定两个整数 n 和 k,返回 1 … n 中所有可能的 k 个数的组合。
示例:
输入: n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
class Solution:
def combine(self, n: int, k: int) -> [[int]]:
# 回溯法
res = []
def backtrack(i, k, tmp):
if k == 0:
res.append(tmp)
return
for j in range(i, n+1):
backtrack(j+1, k-1, tmp+[j])
backtrack(1, k, [])
return res
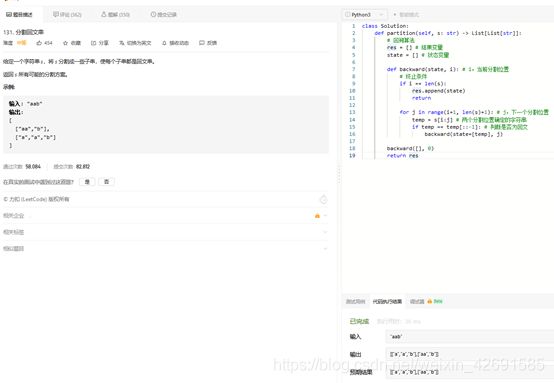
131. 分割回文串
给定一个字符串 s,将 s 分割成一些子串,使每个子串都是回文串。
返回 s 所有可能的分割方案。
示例:
输入: “aab”
输出:
[
[“aa”,“b”],
[“a”,“a”,“b”]
]
class Solution:
def partition(self, s: str) -> List[List[str]]:
# 回溯算法
res = [] # 结果变量
state = [] # 状态变量
def backward(state, i): # i,当前分割位置
# 终止条件
if i == len(s):
res.append(state)
return
for j in range(i+1, len(s)+1): # j,下一个分割位置
temp = s[i:j] # 两个分割位置确定的字符串
if temp == temp[::-1]: # 判断是否为回文
backward(state+[temp], j)
backward([], 0)
return res
22. 括号生成
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
示例:
输入:n = 3
输出:[
“((()))”,
“(()())”,
“(())()”,
“()(())”,
“()()()”
]
class Solution:
def generateParenthesis(self, n: int) -> List[str]:
#回溯法
result = []
def backtrack(left, right, tmp):
if right > left or left > n: return
if left + right == 2 * n:
result.append(tmp)
return
backtrack(left + 1, right, tmp + '(')
backtrack(left, right + 1, tmp + ')')
backtrack(0, 0, '')
return result