向量迭代求’最大‘特征值和对应的特征向量(python,数值积分)

第二十五篇 向量迭代求’最大‘特征值和对应的特征向量

特征值方程的解

由于方程两边都存在未知向量{x}，可以看出特征值问题的解法本质上是一种迭代。之前已经提到过这样一种方法，涉及到找出特征多项式的根。第二类为“转化方法”，矩阵[A]被迭代变换为一个新矩阵，例如[A∗]，它具有与[A]相同的特征值。好在这些特征值比原始矩阵的特征值更容易计算。第三类方法为“向量迭代”方法，就像之前对非线性方程解的迭代代换一样，对方程左边的{x}做出猜测值，形成乘积[a]{x}，并与右边再做比较。然后反复调整猜测值，直到达成一致。

向量迭代

这个过程有时被称为“幂”方法，只能找到它所作用的矩阵的最大(绝对)特征值和相应的特征向量。然而，通过人类的智慧，这并不会限制对问题的探究，因为对初始矩阵的修改将使其他特征解能够被找到。向量迭代的收敛速度取决于特征值的性质。
具体实例：
求出下面矩阵的’最大‘特征值和对应的特征向量

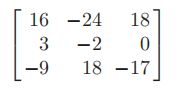
特征值方程为下面的形式

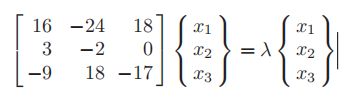
设初始值x={1,1,1}T
左手边的矩阵向量乘积为

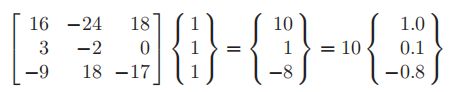
在这里，我们将结果向量正交化，除以其中最大数的绝对值。然后将规范化的{x}用于下一次迭代，因此第二次迭代成为

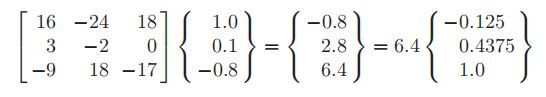
第三次为

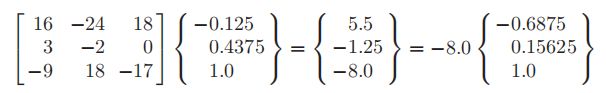
第四次为

说明收敛于特征值λ =−8，即特征值中绝对值最大的数。
程序如下：
分为一个主程序和一个检查是否收敛的子程序checkit

#'最大'特征值和它的特征向量的迭代替换
import numpy as np
import B
n=3;tol=1.0e-5;limit=100
a=np.array([[10,5,6],[5,20,4],[6,4,30]],dtype=np.float)
x1=np.zeros((n,1))
x=np.ones((3,1),dtype=np.float)
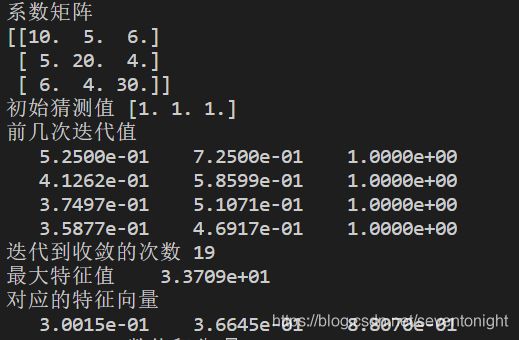
print('系数矩阵')
print(a[:])
print('初始猜测值',x[:,0])
print('前几次迭代值')
iters=0
while(True):
    iters=iters+1
    x1[:]=np.dot(a,x)
    big=0.0
    for i in range(1,n+1):
        if abs(x1[i-1,0])>abs(big):
            big=x1[i-1,0]
    x1[:,0]=x1[:,0]/big
    if  B.checkit(x1,x,tol)==True or iters==limit:
        break
    x[:,0]=x1[:,0]
    if iters<5:
        for i in range(1,n+1):
            print("{:13.4e}".format(x[i-1,0]),end=" ")
        print(end="\n")
l2=np.linalg.norm(x1)
x1[:,0]=x1[:,0]/l2
print('迭代到收敛的次数',iters)
print('最大特征值',"{:13.4e}".format(big))
print('对应的特征向量')
for i in range(1,n+1):
    print("{:13.4e}".format(x1[i-1,0]),end=" ")

checkit

def checkit(loads,oldlds,tol):
#检查多个未知数的收敛
  neq=loads.shape[0]
  big=0.0
  converged=True
  for i in range(1,neq+1):
    if abs(loads[i-1,0])>big:
      big=abs(loads[i-1,0])
  for i in range(1,neq+1):
    if abs(loads[i-1,0]-oldlds[i-1,0])/big>tol:
      converged=False
  checkit=converged
  return  checkit

终端输出结果如下