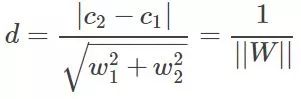c++实现svm_机器学习（四）-SVM支持向量机
1 学习记录
1.1 支持向量机
https://blog.csdn.net/jasonzhoujx/article/details/81904933
核心：边界最大化
对于仅仅使用分割线划分分界线可能会存在多解的问题，SVM提供了改进这个问题的方法：不再画一条细线来区分分类，而是画一条到最近点的边界、有宽度的线条。在支持向量机中，选择边界最大的那条线是模型的最优解。支持向量机其实就是一个边界最大化评估器。
1.2 SVM理解
支持向量机通俗导论：https://blog.csdn.net/v_july_v/article/details/7624837#t28
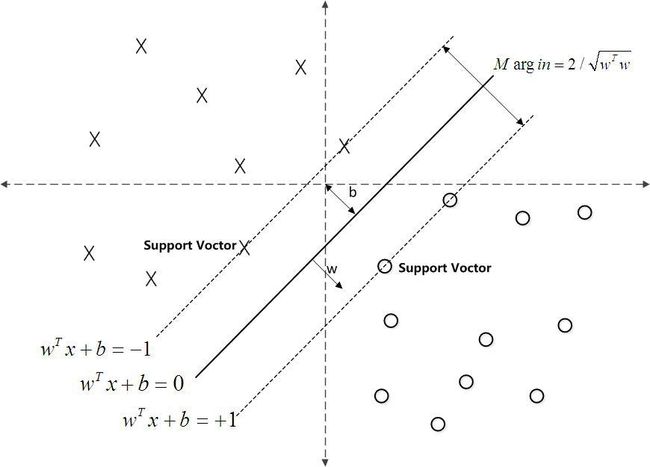
在二分类问题中，SVM的本质是寻得一个分割超平面，使margin最大化，见下图，margin就是切割超平面离最近点的距离 ；SVM的核心问题就是找到这一超平面，使得margin的值最大。
超平面：在一维空间里就是一个点，在二维空间里就是一条直线，三维空间里就是一个平面，可以如此想象下去，如果不关注空间的维数，这种线性函数还有一个统一的名称——超平面（Hyper Plane）！
假设超平面公式：
其中W转置后是横向量，x为纵向量。
在2维特征向量X=(x1,x2) , 把b假设w0 ,
那么超平面方程就变成了 : w0+w1x1+w2x2=0
右上方点满足 : w0+w1x1+w2x2>0
同理，左下点满足 : w0+w1x1+w2x2<0
经过对weight参数的调整，使得
H1:w0+w1x1+w2x2>=1 for y = +1
H2:w0+w1x1+w2x2<=1 for y = - 1 (用y的+1代表一类，-1代表另一类)
综上两式
yi(w0+w1x1+w2x2)>=1,∀i
扩展开来，即得到：对于所有不是支持向量的点，有：
引入平行直线距离公式：
其中
根据SVM的思想，即计算出样本距离i个平面的最小距离中最大值对应的平面，即超平面,也是d最大的最优解。
详解SVM核心公式参考：
https://blog.csdn.net/CSDN_Black/article/details/79446504
1.3 带松弛变量的SVM
对于很多情况下,无法构造能将数据完美分割的超平面。或者为了整体更好的结果，我们并不需要属于同一标签的点都严格处在超平面的同一边。此时我们就需要引入松弛变量ξi(≥0)，对应数据点允许偏离的functional margin量，也就是支持向量。如果ξi可以任意大的话，那么任何超平面都会符合条件。把ξi加入到目标函数中，即得到松弛SVM函数模型：
2 代码理解
2.1 sklearn.datasets.make_blobs
https://scikit-learn.org/stable/modules/generated/sklearn.datasets.make_blobs.html
sklearn.datasets.make_blobs(n_samples=100, n_features=2, centers=None, cluster_std=1.0, center_box=(-10.0, 10.0), shuffle=True, random_state=None)[source]
常被用来生成聚类算法的测试数据，make_blobs会根据用户指定的特征数量、中心点数量、范围等来生成几类数据，用于测试聚类算法的效果。
其中：
n_samples是待生成的样本的总数。
n_features是每个样本的特征数。
centers表示类别数。
cluster_std表示每个类别的方差。
返回值：
X: 生成的[n_samples, n_features]数组样本
y: 样本标签，[n_samples]数组.
xlim = ax.get_xlim()# X轴的取值范围
ylim = ax.get_ylim()# y轴的取值范围
# create grid to evaluate model
x = np.linspace(xlim[0], xlim[1], 30)
y = np.linspace(ylim[0], ylim[1], 30)
Y, X = np.meshgrid(y, x)# 矩阵化，得到30*30的网格矩阵
# X 30*30 矩阵
# X.ravel() 1维矩阵 shape为（900，）
# [X.ravel(), Y.ravel()] =[array([1x900])，array([1x900])] 长度为2的list，每个元素由1维矩阵 shape为（900，）组成
# np.vstack([X.ravel(), Y.ravel()]) = [[1x900],[1x900]] ,2x900矩阵
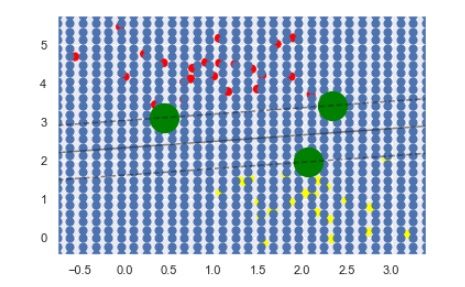
# 根据数据所在区域的坐标矩阵图，图中蓝色的点即xy的散点图
xy = np.vstack([X.ravel(), Y.ravel()]).T
2.2 PCA
目标是通过某种线性投影，将高维的数据映射到低维的空间中表示，即把原先的n个特征用数目更少的m个特征取代，新特征是旧特征的线性组合。并期望在所投影的维度上数据的方差最大，尽量使新的m个特征互不相关。从旧特征到新特征的映射捕获数据中的固有变异性。以此使用较少的数据维度，同时保留住较多的原数据点的特性。
PCA降维的准则有以下两个：
- 最近重构性：重构后的点距离原来的点的误差之和最小
- 最大可分性：样本点在低维空间的投影尽可能分开
from sklearn.svm import SVC
from sklearn.decomposition import PCA
from sklearn.pipeline import make_pipeline
# PCA 降维
pca = PCA(n_components=100, whiten=True, random_state=42)
svc = SVC(C=1.0, kernel='rbf', gamma='auto', coef0=0.0)PCA(copy=True, iterated_power='auto', n_components=150, random_state=42,
svd_solver='auto', tol=0.0, whiten=True)
PCA主要参数:
n_components：这个参数可以帮我们指定希望PCA降维后的特征维度数目;
copy： 表示是否在运行算法时，将原始数据复制一份。默认为True，则运行PCA算法后，原始数据的值不会有任何改变。因为是在原始数据的副本上进行运算的;
whiten ：判断是否进行白化，就是对降维后的数据的每个特征进行归一化，让方差都为1;
vd_solver：即指定奇异值分解SVD的方法, 一般的PCA库都是基于SVD实现的。有4个可以选择的值：{‘auto’, ‘full’, ‘arpack’, ‘randomized’}。
- 'randomized' 一般适用于数据量大，数据维度多同时主成分数目比例又较低的PCA降维，它使用了一些加快SVD的随机算法。
- 'full' 则是传统意义上的SVD，使用了scipy库对应的实现。
- 'arpack' 和randomized的适用场景类似，区别是randomized使用的是scikit-learn自己的SVD实现，而arpack直接使用了scipy库的sparse SVD实现。当svd_solve设置为'arpack'时，保留的成分必须少于特征数，即不能保留所有成分。
- 默认是'auto'，即PCA类会自己去在前面讲到的三种算法里面去权衡，选择一个合适的SVD算法来降维。一般来说，使用默认值就够了。
https://www.imooc.com/article/44218
https://www.cnblogs.com/solong1989/p/9681788.html
sklearn.svm.SVC(C=1.0, kernel='rbf', degree=3, gamma='auto', coef0=0.0, shrinking=True, probability=False,tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape=None,random_state=None)
参数：
主要调节的参数有：C、kernel、degree、gamma、coef0。
C：C-SVC的惩罚参数C?默认值是1.0,C越大，相当于惩罚松弛变量，希望松弛变量接近0，即对误分类的惩罚增大，趋向于对训练集全分对的情况，这样对训练集测试时准确率很高，但泛化能力弱。C值小，对误分类的惩罚减小，允许容错，将他们当成噪声点，泛化能力较强。
kernel ：核函数，默认是rbf，可以是‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’
0 – 线性：u'v
1 – 多项式：(gamma*u'*v + coef0)^degree
2 – RBF函数：exp(-gamma|u-v|^2)
3 –sigmoid：tanh(gamma*u'*v + coef0)
degree ：多项式poly函数的维度，默认是3，选择其他核函数时会被忽略。
gamma ： ‘rbf’,‘poly’ 和‘sigmoid’的核函数参数。默认是’auto’，则会选择1/n_features
coef0 ：核函数的常数项。对于‘poly’和 ‘sigmoid’有用。
probability ：是否采用概率估计？.默认为False
shrinking ：是否采用shrinking heuristic方法，默认为true
tol ：停止训练的误差值大小，默认为1e-3
cache_size ：核函数cache缓存大小，默认为200
class_weight ：类别的权重，字典形式传递。设置第几类的参数C为weight*C(C-SVC中的C)
verbose ：允许冗余输出
max_iter ：最大迭代次数。-1为无限制
decision_function_shape ：‘ovo’, ‘ovr’ or None, default=None3
random_state ：数据洗牌时的种子值，int值
3 课后作业
3.1 训练SVM
建立寻pipeline
from sklearn.svm import SVC
from sklearn.decomposition import PCA
from sklearn.pipeline import make_pipeline
pca = PCA(n_components=100, whiten=True, random_state=42)
svc = SVC(C=1.0, kernel='rbf',gamma='auto', coef0=0.0)
model = make_pipeline(pca, svc)使用训练好的SVM做预测
model = grid.best_estimator_
yfit = model.predict(Xtest)生成性能报告
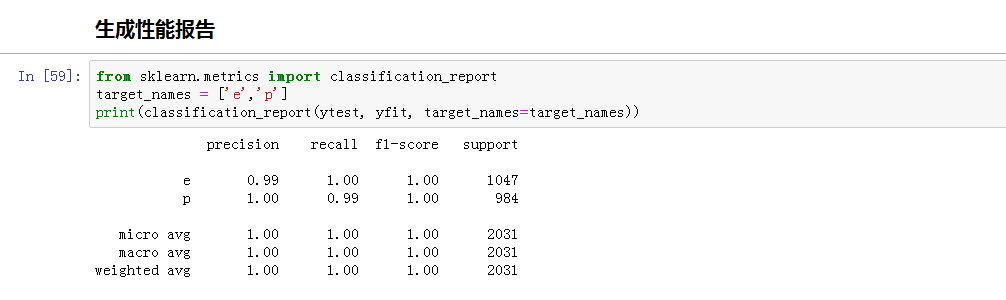
from sklearn.metrics import classification_report
target_names = ['e','p']
print(classification_report(ytest, yfit, target_names=target_names))
sklearn中的classification_report函数用于显示主要分类指标的文本报告。在报告中显示每个类的精确度，召回率，F1值等信息。
主要参数:
y_true：1维数组，或标签指示器数组/稀疏矩阵，目标值。
y_pred：1维数组，或标签指示器数组/稀疏矩阵，分类器返回的估计值。
labels：array，shape = [n_labels]，报表中包含的标签索引的可选列表。
target_names：字符串列表，与标签匹配的可选显示名称（相同顺序）。
sample_weight：类似于shape = [n_samples]的数组，可选项，样本权重。
digits：int，输出浮点值的位数。
https://blog.csdn.net/akadiao/article/details/78788864
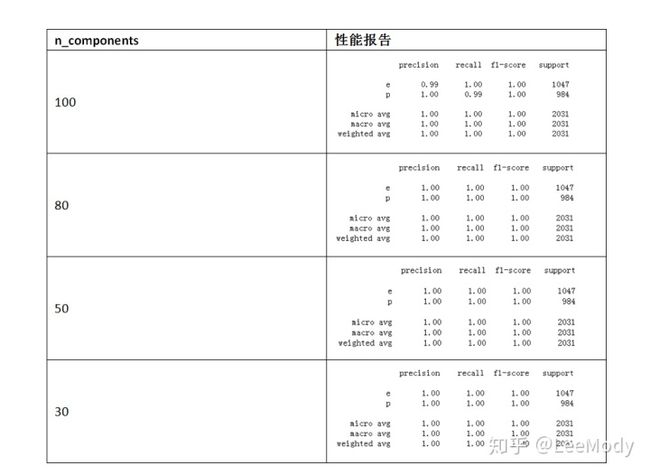
3.4 PCA参数调整
尝试pca = PCA(n_components=100, whiten=True, random_state=42)中n_components的值，100，80，50，30
4 小结
理解SVM公式推导以及约束条件的原理；
理解带松弛变量的SVM的原理，以及松弛参数在实际问题中的作用；
学习和练习了课程中使用到的库与方法；
最后在课后作业中，通过对PCA 参数的选择，得到不同的训练结果和测试结果。
参考
贪心学院特训营：
机器学习特训营zhuanlan.zhihu.com
详解SVM核心公式：
https://blog.csdn.net/CSDN_Black/article/details/79446504blog.csdn.net支持向量机通俗导论：
https://blog.csdn.net/v_july_v/article/details/7624837#t28blog.csdn.netsklearn.datasets.make_blobs官方网址：
sklearn.datasets.make_blobs - scikit-learn 0.21.2 documentationscikit-learn.org
classification_report解释：
https://blog.csdn.net/akadiao/article/details/78788864blog.csdn.net