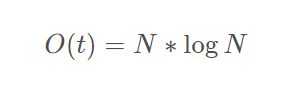数据结构——堆
数据结构————堆
目录
- 堆的概念及其结构
- 堆的实现
- 堆排序(HeapSort)
- 堆的Init和Destroy
- 堆的插入
- 取堆头数据
- 堆顶弹出Pop
- 堆打印
注:这里的堆还没牵扯到优先级队列
一.堆的概念及其结构
本章用到的这种工具叫做二叉堆,为了方便叫法,我们一般直接称其为堆——Heap
1.概念
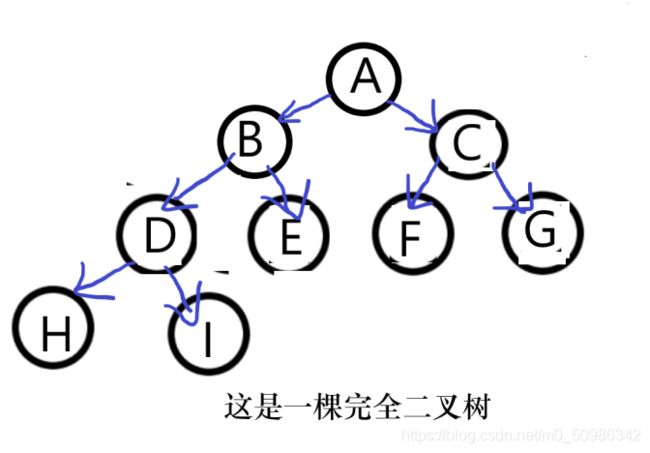
既然是二叉堆,顾名思义,它其实就是基于完全二叉树结构的一种数据结构 如果你不知道二叉树,=W=那就。。
2.结构
结构有物理结构和逻辑结构。
物理结构
一般我们构建堆时,考虑到数组的方便性(容易找到父亲和儿子的位置关系,不需要使用指针)的情况下,我们优先使用数组来实现堆。
逻辑结构
既然是基于完全二叉树,那么这样就好办了。那就是一棵完全二叉树嘛!
这里还是来穿插一下待会我们代码实现中必须熟记的一种关系
对于数组中任意位置X上的元素,其左儿子在位置2X+1上,右儿子在位置2X+2上。它的父亲在 (X-1) / 2上。
基于这样的结构,堆又分为大根堆和小根堆。

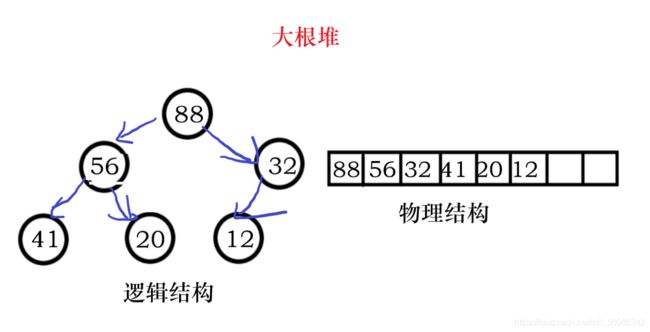
很好理解:
小根堆:父亲总是小于等于孩子
大根堆:父亲总是大于等于孩子
再结合上父亲和孩子的关系:
假设父亲的下标为 parent
则左孩子的下标为 parent * 2 + 1
则右孩子的下标为 parent * 2 + 2
parent = (child - 1)/2
2.堆的实现
在讲这之前,我们必须得先明白一个很重要的算法——“向下调整算法”
这里给出一课完全二叉树

此树满足:
左右子树都是一个完整的小堆 (注意!这个条件很重要!)
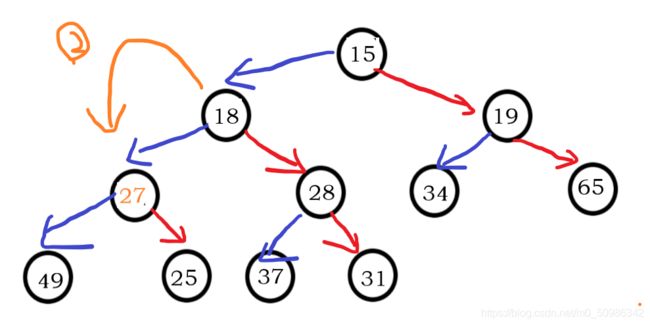
那么该如何将它调整成一个小堆呢?
我们稍加注意,发现27这一混蛋的存在导致了我们问题的存在。
它破坏了小堆结构的规则,那我们就把它干下去!
向下调整算法:
找出左右孩子较小的那个,与父亲比较。如果孩子比父亲小,则进行交换
接着迭代过程,让刚刚交换后的孩子下标位置成为新的父亲,接着往下利用父子位置关系找到新的孩子…
如果父亲已经比孩子小,停止迭代直到最后,当父亲下标为叶子节点时,停止迭代。
按照这一逻辑规则,我们上图:
代码实现:
void Swap(HPDataType* a, HPDataType* b)//交换两个元素
{
HPDataType temp = *a;
*a = *b;
*b = temp;
}
void AdjustDown(HPDataType* a, int size, int parent)
{
int child = parent * 2 + 1; //接口传入的是parent的下标,则我们
//需要孩子的节点
while (child < size)
{
if(child + 1 < size && a[child+1] < a[child])
//在right child不越界的情况下,如果right child
//小于left child,则我们让
//child的下标++,使得这个时候的child指向的是right child
//(更小的那个)
{
child++;
}
//如果child小于parent,则进行交换
if (a[parent] > a[child])
{
Swap(&a[parent], &a[child]);
parent = child;//迭代,让parent变成刚刚child的位置
child = parent * 2 + 1;//继续计算child的位置
}
else//如果parent大于或等于child 则不需要再继续向下调整
{
break;
}
}
}
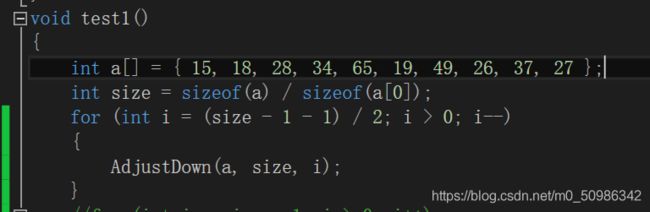
OK,这就是向下调整算法,咱们可以自己创建一个数组玩一玩看看这个效果如何
这边就直接用刚刚图片里面的例子来试试吧
int a[] = { 27, 15, 19, 18, 28, 34, 65, 49, 25, 37 };
按照我们的逻辑,a数组在进行向下调整之后应该变为
a[] = 15 18 19 25 28 34 65 49 27 37 31
向下调整之前:
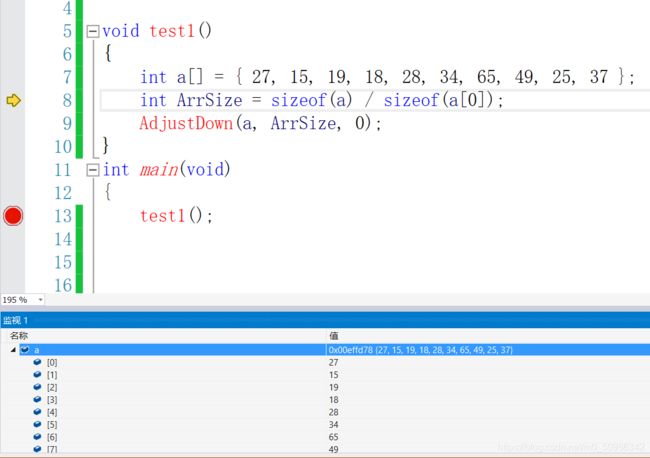
之后:
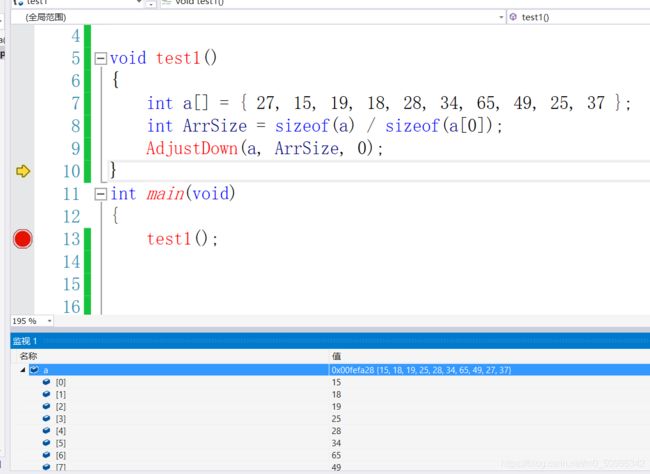
那么!我们搞定了这一算法后,我们可以回到刚刚的问题
如何实现一个堆呢?
在刚刚的问题中,我强调了一个很关键的信息。那就是基于刚刚的算法,我们这棵完全二叉树的root(根)的左右两棵子树,都满足是一个小堆。
而如果我给你一棵随便的完全二叉树,这一算法就不能就这么简单的从 root 开始了
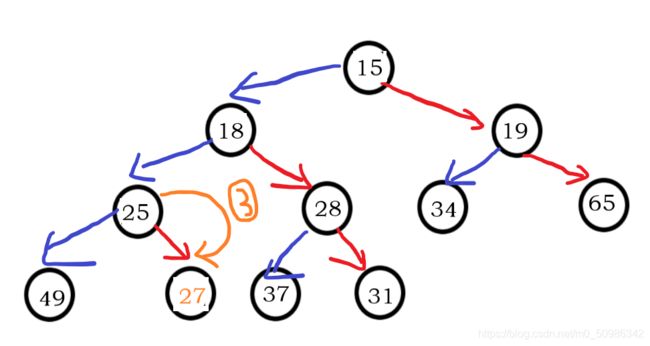
就拿刚刚的数组来举例子,我们将它稍微改进一下~
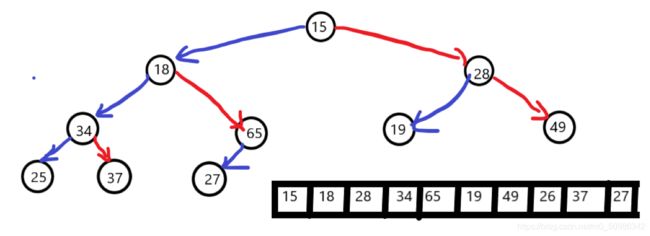
这个时候,我们发现这已经不满足我们刚刚的——“右俩子树是小堆的情况”
如果我们再从下标为0的位置向下调整的话,是行不通的。
那。。咋整呢?
其实这里聪明的你很容易想到,既然不从上面向下调的话,那我从下面最后一个父节点开始进行向下调整不就行了?
具体操作如下:
找到最后一个节点的父亲,也即如果数组长度为X的话,那么最后一个节点的下标位置应该是 (X-1-1)/2
这里解释一下,X-1是最后一个元素的下标,再进行-1操作是我们要找到左孩子的节点,除以2,即找到最后的父节点。这里就是我们上面讲过的父与子的位置关系。
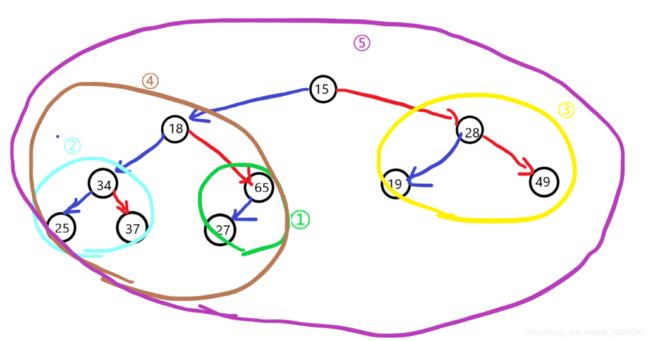
顺着这张图的顺序,依次向下调整。最终,这个"四不像"的堆,最终会被我们调整为之前的样子——一个完整的小堆。
那么构造大堆呢?这里其实也是差不多类似的一种办法
比如下面这棵树:
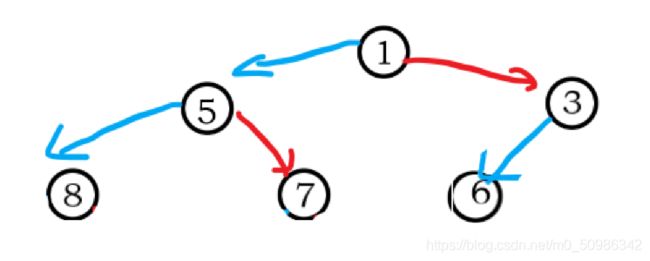
这里有人就会说:" 哎呀这个不就是一个小堆嘛!"
别骂了别骂了QAQ
是的是的。。这里我是想考虑极端情况,将一个小堆弄成大堆,这样更好理解嘛
先回忆一下那个特征————左右子树必须满足是一个堆
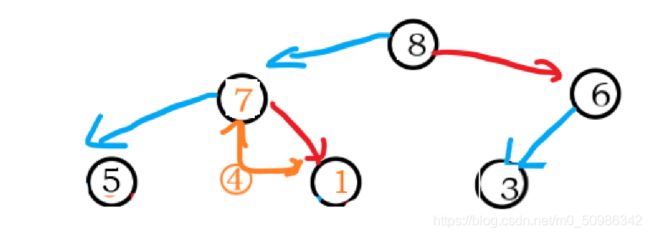
那么好了,既然我想把它调整成一个大堆,那么左右子树则必须满足是个大堆。沿着这个思路,我们只需要从下往上,依次找到每个节点的父亲,然后进行向下调整即可。
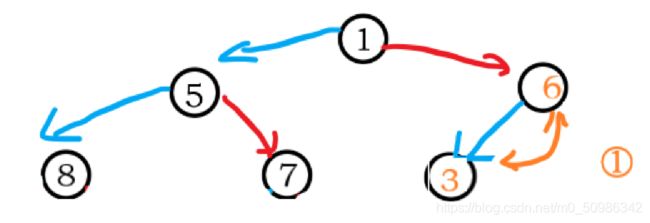
找到8和7中较大的,与5比较,之后交换

找到8和6中较大的,与1比较,之后交换

这里还没完,这里一定要注意了
堆有两个性质:结构性和堆序性 和AVL树一样,对堆的一次操作可能会破坏这两个性质的其0一个
这里就出现了这个问题
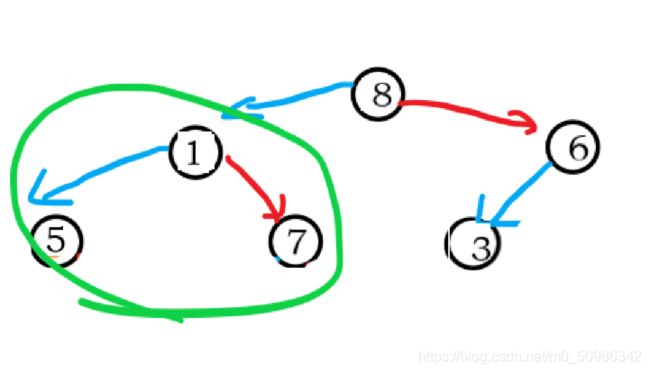
绿色画起来的地方,经过刚刚一波操作后,已经破坏了堆的结构了。这里还得再进行一次向下调整!
3.堆排序(HeapSort)
刚刚的堆构造掌握了之后,我们可以来掌握一个排序算法——堆排序
排序算法有很多,为啥要学习堆排序呢?这里我们得先分析一下其时间复杂度
首先,构建堆的时间复杂度就得需要咱们好好推敲一下。
构建最差情况,我们假设我们要构建一棵满二叉树,它堆高为Hi
每层节点个数为Ni
那么时间复杂度T(N)
可以列出下列的式子:
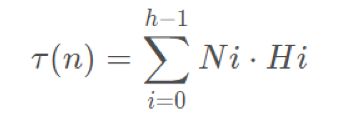
接着我们展开化简一下:
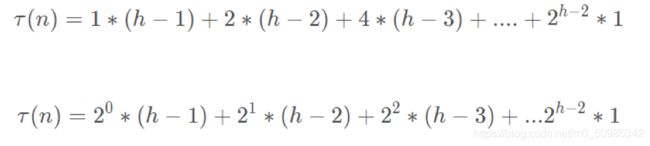
好的,重新舍起你中学所学过的数学知识,这不就是一个等差数列乘以一个等比数列的形式嘛?
有招错位相减想起来了没
错位相减走起来!
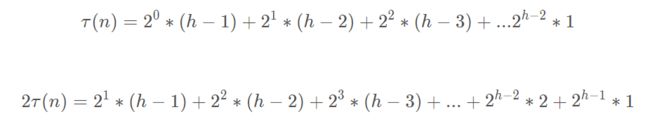
两式相减并化简后
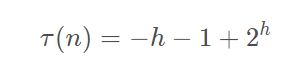
其中,学过二叉树的都知道,高度h我们是可以求出来的
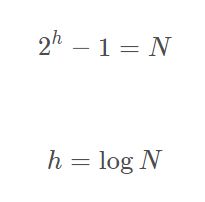
两个式子代入公式中,得到
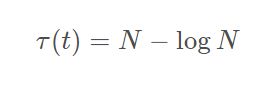
根据大O的时间复杂度计算方法,在这其中,N占据主导地位
最后,我们推出构建堆的时间复杂度为
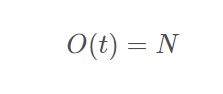
好滴!这样我们就搞定了这个推导。
那我们继续回到堆排序的问题上来,假设我现在要对一个数组调整为升序,我们现在会构建堆了,现在只需要考虑一个很重要的问题:
我们到底是要构建大堆还是小堆的问题
很大的一个陷阱是,作为初学者的我们来说,调整为升序咱们会很自然的想到要调整为小堆。但是恰恰相反,咱们要做升序,得用大堆。
为什么呢?咱们看下下面的图解。
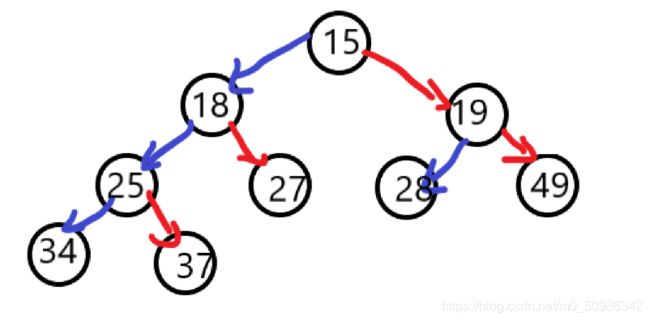
这是一棵小堆树,如果我们要将其上面的数据取出创建出一个升序的数组,取出第一个数据之后(最小的),接着要选出次小的,咋选?
这就牵扯到一个问题,第二层的两个数据,他们两个是没有大小关系的。这么说可能有点抽象,就是说,在我们建堆后,18和19两个元素两者间仅仅只是因为比第一层18大,比第三层所有数据小,进而存在在了第二层。
所以如果我们将15去除掉(这里要用一种方法来去除,待会会提到),然后再进行向下调整出一个新的小堆,选出下一个次小的。但是这里就面临着刚刚说的问题,这里举得例子只是刚好巧了,18被调整到root之后,巧了!整个结构还是小堆。。
没错没错。。这是例子举的不好。。
但是!我还是要讲一下这个问题,如果按照刚刚的思路来说,让18变为新的root之后,整棵树的关系都乱了,这样需要重新再一次建堆*(注意这里不是再进行一次向下调整,本人刚开始学的时候误以为是这样)*
记得刚刚建堆的时间复杂度是多少吗?O(N)啊!那也就是说,最坏情况下,每进行一次寻找最小数据,都要花费O(N)的时间,那就是O(N^N)的时间复杂度,天啊这也有点太大了。
既然我们放弃选择排序选择堆排序,那么我们的初衷肯定是要更快(选择排序O(N^2)),我们既然都建了一个这么复杂的堆,那么肯定要达到目的。
那么来讲讲构建为啥要构建大堆来进行排序吧。
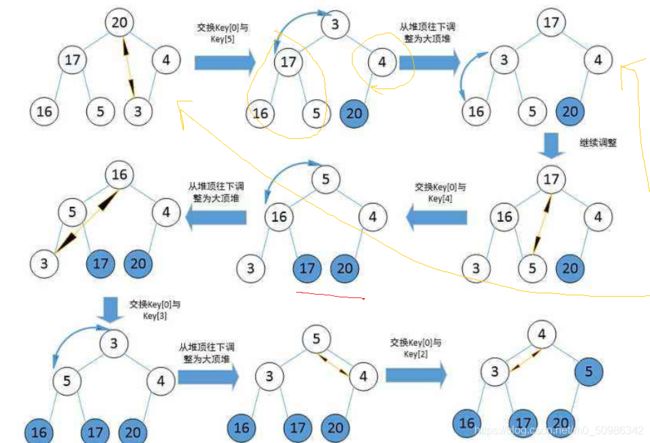
首先,我们先构造一个大堆
第一个元素则是我们要的最大的数字,这个时候我们将它与最后一个元素交换
进行向下调整,只不过这个时候我们的数组元素大小得 -1,不用再去考虑刚刚我们换下去的数字
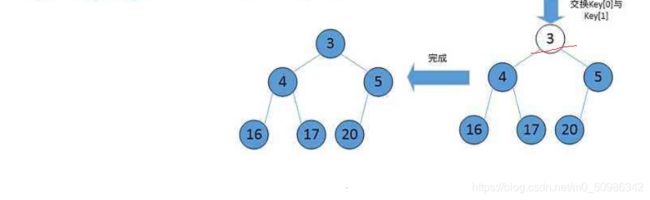
它已经排序好了。
重复这个过程,直到最后一个元素下标到达0时,结束
void HeapSort(HPDataType* a, int n)//如果要排序升序,要建大堆
{
//建堆
//时间复杂度:
//假设树有N个节点。树的高度为:logN
for (int i = ((n - 1) - 1)/2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
--end;
}
}
肯定要小于 O(n^2)吧,这样一来我们就达到目的了。
4.堆的Init和Destory
HeapInit(初始化堆)
开始我们说过了,堆的物理结构是一个数组,那么就好办了,这个跟顺序表的构建其实是很类似的
不过要注意最后记得要建堆罢了
void HeapInit(Heap* php, HPDataType* a, int n)//初始化 堆
{
php->_a = (HPDataType*)malloc(sizeof(HPDataType)*n);
memcpy(php->_a, a, sizeof(HPDataType)*n);
php->_size = n;
php->_capacity = n;
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
AdjustDown(php->_a, php->_size, i);
}
}
HeapDestory (堆的摧毁)
没啥可说的
void HeapDestory(Heap* php)//堆--摧毁
{
assert(php);
free(php->_a);
php->_a = NULL;
php->_capacity = php->_size = 0;
}
5.堆的插入
其实插入并没有什么难点,但是始终要注意一点(堆的特性),再进行一次堆插入后,这个堆的结构就会被破坏
所以,这里介绍一个新的算法——向上调整(AdJustUp)
这里,我给这个大堆插入了一个新节点——9
插入完毕后,我们得让它重新回到大堆的样子,这里介绍一个向上调整算法
它和向下调整不同,因为在堆的结构中,新节点9的出现只影响它那一溜~~的路线
也就是我用绿色画出来的这条

那么只需要调整这一溜就好了!
void AdjustUp(HPDataType* a, int n, int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
整体代码呢。:
void HeapPush(Heap* php, HPDataType x)
{
assert(php);
if (php->_capacity == php->_size)
{
php->_capacity *= 2;
HPDataType* tmp = (HPDataType*)realloc(php->_a, sizeof(HPDataType)*php->_capacity);
php->_a = tmp;
}
php->_a[php->_size++] = x;
AdjustUp(php->_a,php->_size,php->_size-1);
}
6.返回堆头
简单啦~
HPDataType HeapTop(Heap* hp)
{
assert(hp);
assert(hp->_size > 0);
return hp->_a[0];
}
7.堆的弹出
简单简单,记得重新再向下调整就行了
void HeapPop(Heap* hp)
{
assert(hp);
assert(hp->_size > 0);
Swap(&hp->_a[0], &hp->_a[hp->_size - 1]);
hp->_size--;
AdjustDown(hp->_a, hp->_size, 0);
}
8.堆的打印
QAQ太简单了以至于我懒了
void HeapPrint(Heap* hp)
{
assert(hp);
for (int i = 0; i < hp->_size; i++)
{
printf("%d ", hp->_a[i]);
}
printf("\n");
}
9.最终整体代码
#pragma once
#include //今儿又是活力满满的一天呢~
#define _CRT_SECURE_NO_WARNINGS 1
#include "Heap.h"
void Swap(HPDataType* a, HPDataType* b)
{
HPDataType temp = *a;
*a = *b;
*b = temp;
}
//向下调整算法
void AdjustDown(HPDataType* a, int size, int parent)
{
int child = parent * 2 + 1;
while (child < size)
{
if(child + 1 < size && a[child+1] < a[child])
{
child++;
}
if (a[parent] > a[child])
{
Swap(&a[parent], &a[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void AdjustUp(HPDataType*a, int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void HeapCreate(Heap* hp, HPDataType* a, int n)
{
assert(hp);
hp->_a = (HPDataType*)malloc(sizeof(HPDataType)*n);
if (hp->_a == NULL)
{
printf("Malloc Fail!\n");
exit(-1);
}
//需要将hp->_a做成堆,不改变传进来的数组a
memcpy(hp->_a, a, sizeof(HPDataType)*n);
hp->_size = hp->_capacity = n;
//建堆
for (int i = (hp->_size - 1 - 1) / 2; i >= 0; --i)
{
AdjustDown(hp->_a,hp->_size,i);
}
}
void HeapDestory(Heap* hp)
{
assert(hp);
free(hp->_a);
hp->_a = NULL;
hp->_capacity = hp->_size = 0;
}
void HeapPush(Heap* hp, HPDataType x)
{
assert(hp);
if (hp->_capacity == hp->_size)
{
HPDataType* temp = realloc(hp->_a, sizeof(HPDataType) * hp->_capacity * 2);
if (temp == NULL)
{
printf("Realloc Fail\n");
exit(-1);
}
hp->_a = temp;
hp->_capacity = hp->_capacity * 2;
}
hp->_a[hp->_size] = x;
hp->_size++;
/*for (int i = (hp->_size - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(hp->_a, hp->_size, i);
}*/
int i = hp->_size - 1;
AdjustUp(hp->_a, i);
}
void HeapPrint(Heap* hp)
{
assert(hp);
for (int i = 0; i < hp->_size; i++)
{
printf("%d ", hp->_a[i]);
}
printf("\n");
}
void HeapPop(Heap* hp)
{
assert(hp);
assert(hp->_size > 0);
Swap(&hp->_a[0], &hp->_a[hp->_size - 1]);
hp->_size--;
AdjustDown(hp->_a, hp->_size, 0);
}
HPDataType HeapTop(Heap* hp)
{
assert(hp);
assert(hp->_size > 0);
return hp->_a[0];
}
嘿嘿,就分享就到这里啦~有错误请及时纠正我批评我噢