开发成长之路（7）-- C++从入门到开发（C++知名库：STL入门·容器（二））

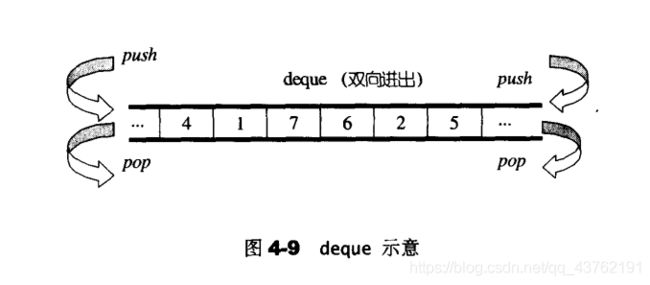
deque

vector是单向开口的连续线性空间，deque则是一种双向开口的连续线性空间。
所谓双向开口，也就是说可以在头尾两端进行插入和删除操作。

vector当然也可以做头部操作，但是其头部操作效率奇差！！！
无法被接受。
（这点以前居然都没有发现！！！）

deque没有所谓容量的观念，因为它是动态的以分段连续空间组合而成，随时可以增加一段新的空间并链接起来。因此，deque没有必要提供所谓的空间保留功能。

但是呢，为什么我们更多的选用vector而非deque呢？因为它的指针实在是太麻烦了。我们后面就知道了。

除非必要，我们应尽可能的选择使用vector而非deque。对deque进行的排序操作，为了最高效率，可以将deque完整的复制到一个vector身上，将vector排序后，再复制回deque。

不要被事务的表面现象锁迷惑，你看它是分段连续线性空间，就以为它是vector和list的结合体，取长补短？其实不然。
为了维持整体连续的假象，数据结构的设计及迭代器前进后退等操作都颇为繁琐。

---

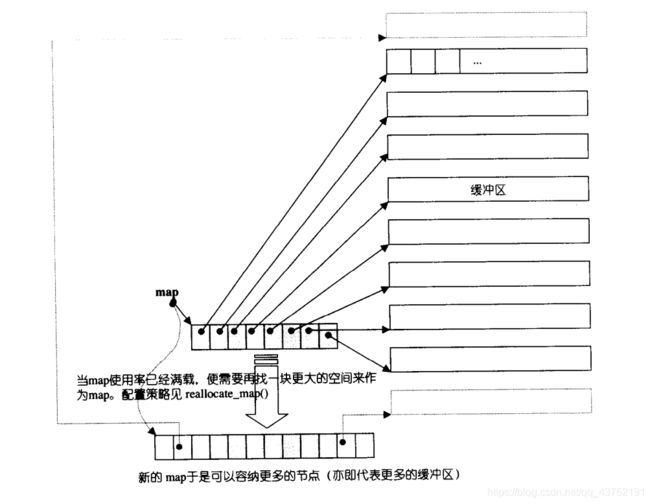
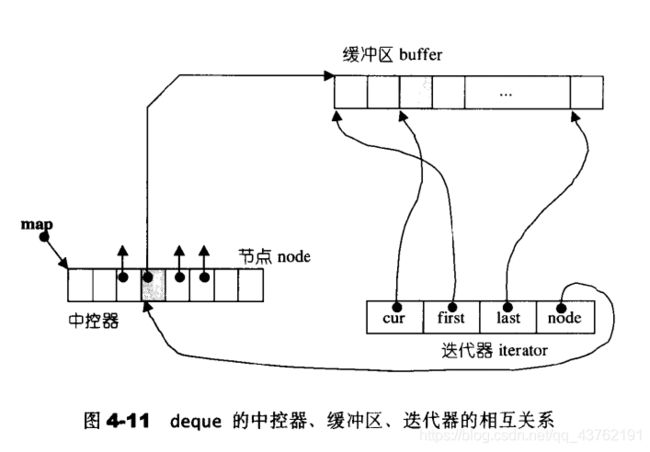
deque的中控器

deque采用一块所谓的map映射，来看吧：

template <class T,class Alloc = alloc,size_t BufSiz = 0>
class deque{
     
public:
	typedef T value_type;
	typedef value_type* pointer;
	···
protected:
	//元素的指针的指针
	typedef pointer* map_pointer;

protected:
	map_pointer map;	
	//指向map，map是块连续空间，其内的每个元素都是一个指针，指向一块缓冲区
	
	size_type map_size;
	//map内可容纳多少指针
}

看得我尴尬症都犯了。

此外，deque还维护start、finish两个迭代器，分别指向第一缓冲区的第一个元素和最后缓冲区的最后一个元素（的下一个位置）。
此外，它当然也必须记住目前map的大小，一旦map的空间不足，必须要重新配置一个更大的map。

---

stack – 栈

什么是栈？怎么说呢，我觉得我真应该先写数据结构专栏。失策失策！！！
栈是一种先进后出的数据结构，它只有一个接口。
只能从一端加入元素，从那一端移除元素，所以并不被允许有其他方法来存取元素。
换言之，stack不允许有遍历行为。

将元素推入stack的方式称为push，将元素退出stack的操作称为pop。

以某种既有容器作为底部结构，将其接口改变，使之符合“先进后出”的特性，形成一个stack，是很容易做到的。

deque是双向开口数据结构，若以deque为底部结构并封闭其头端开口。
便轻而易举形成了一个stack、
（不知道为什么，我觉得好糟糕哦，vector是不能做吗？）

还是等我过两篇写数据结构的时候再说吧。

---

除deque之外，list也是双向开口的数据结构。以list为底的stack被称作链栈。

嘿我就挺纳闷儿，为什么就非要双向开口的数据结构？？？

---

queue – 队列

队列，是一种先进先出结构，只能从一端加入元素，从另一端移除元素，所以并不被允许有其他方法来存取元素。
换言之，queue不允许有遍历行为。

那这个跟上面的stack其实没多大区别，只不过一个是后进先出，一个是先进先出的罢了。那为什么也要双向开口的数据结构呢？

---

heap是什么

heap并不属于STL容器组件，它是个“幕后白手”，扮演priority queue的助手。

顾名思义，那个queue允许用户以任何次序插入数据，但是在插入的时候会根据优先级进行排序，以保证取出的时候是按照优先级排序的。

如果以List作为这个优先级队列的底层机制，那么排序将会很麻烦，如果以二叉搜索树的话，未免大材小用了。
而难度夹在中间的binary heap便是不二人选了。

所谓binary heap,就是一种完全二叉树，整棵树除了底层节点外，都是填满的，从左至右又不得又间隙。

苍白无力的文字啊，来看张图实在：

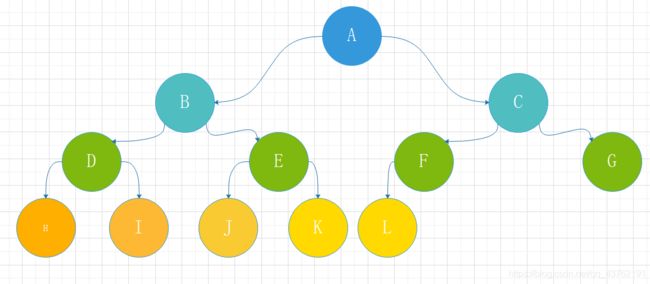
简单明了吧，可以用想象下面有一个数组来存储所有节点，以树根节点作为数组的[0]位置，可以发现，任何一个节点 [i] 的左子节点必位于 [2i] 处，其右子节点必位于 [2i+1] 处。
而任何一个节点 [k]，其父节点必位于 [k/2] 处。

通过这简单的规则，咱就种了一棵树，完全二叉树。
而这颗二叉树需要能动态的增加节点，所以采用vector作为这棵树的底层土壤是个理想的选择。

根据元素排列方式，heap可以分为max-heap和min-heap。STL供应的是max-heap,最大值在头结点。

heap算法

push_heap算法（尾端插入元素）
本来是自己画了图，但是理解了书中的图之后，发现他的图更有一番风味。

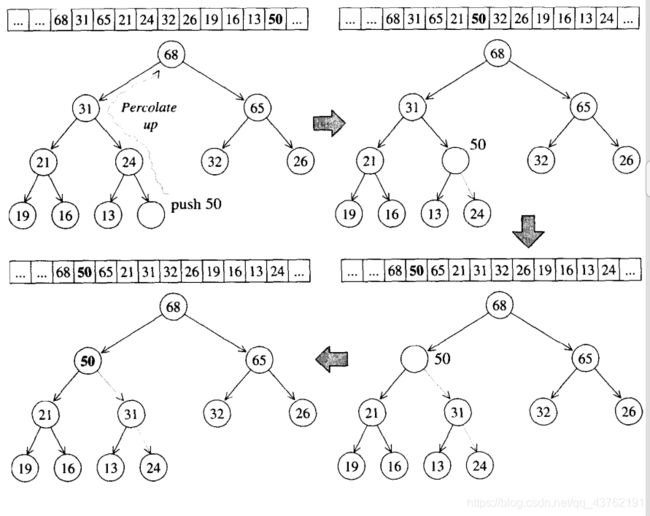
原先我也疑惑于为何同一级中左边的节点会比右边节点大，后来我想明白了。
在插入过程中，这个顺序被打乱是难以避免的，况且这个排序于取出数据并无影响，所以没必要在做额外工作对树的底层做那么精细的排序。

如果还是不理解，先看下去，慢慢的就会茅塞顿开。

在尾部插入时，总是将节点插入到最底层的最右节点，不管你要插入的数据右多大，见上图第一个步骤。
插入之后执行上溯操作，将新节点拿来与父节点进行比较，如果“青出于蓝胜于蓝”，那么将父子节点互换位置。见上图第二个步骤。
之后持续执行上一个步骤，直到不再互换位置。见上图三、四个步骤。
至于下面被打乱的顺序，不用担心，乱中有序。

正是由于这波操作，使得同一级会出现左边的节点比右边的大的情况。

下面来看一下算法的实现细节：

//该函数接受两个迭代器，用来表现一个heap底部容器的头尾，并且新元素已经插入到底部容器的最尾端。

template <class RandomAccessIterator>
inline void push_heap(RandomAccessIterator first,RandomAccessIterator last)
{
     
	__push_heap_aux(first,last,distance_type(first),value_type(first));/*这俩type在上一篇提到了，不知道也就算了吧，毕竟上一篇也不短*/
}

template <class RandomAccessIterator,class Distance,class T>
inline void __push_heap_aux(RandomAccessIterator first,RandomAccessIterator last,Distance*,T*)
{
     
	__push_heap(first,Distance((last-first)-1),Distance(0),T(*(last - 1)));	//(last-first)-1，容器最尾端
}

template <class RandomAccessIterator,class Distance,class T>
void __push_heap(RandomAccessIterator first,Distance holeIndex,Distance topIndex,T value)
{
     
	Distance parent = (holeIndex - 1)/2;	//找出父节点
	while(holeIndex > topIndex && *(first+parent)<value)	//尚未到达顶端，且父节点小于新值，这个循环将父值不断下调
	{
     
		*(first + holeIndex) = *(first + parent);	//令新值为父
		holeIndex = parent;	//调节洞号，向上提升至父节点
		parent = (holeIndex -1)/2;	//新洞的父节点
	}
	*(first + holeIndex) = value;	//令洞值为新值，完成插入操作
}

看下来，果然会茅舍顿开吧。

pop_heap算法（头部插入元素）
看完上面的插入，可能会有人觉得这样打乱顺序的话取出会有问题，其实会有吗？不知道，看下去。

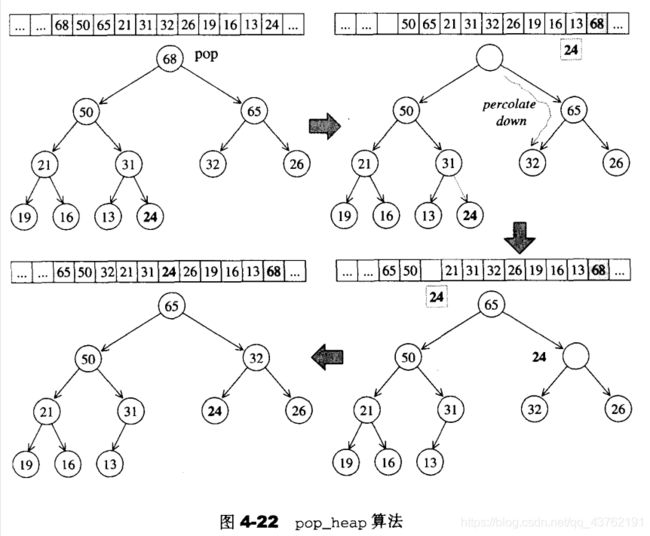
还是用书上的图啊。
取出元素时，首先将1根节点拿下来，留下一个洞洞，见上图第一步到第二步。
还要将当前树的最后一个节点拿下来，并将根节点放到尾节点在容器中的位置。见上图步骤二。
接下来将尾节点和原根节点的两个子节点比较大小，将大的那个推上根节点。见上图步骤三。同样留下一个洞洞。
循环这个“向下流放”的过程，直到原尾结点插入树中或者到了最底层。见上图步骤四。

看懂了这个图之后我们来看算法的实现细节：

template <class RandomAccessIterator>
inline void pop_heap(RandomAccessIterator first,RandomAccessIterator last)
{
     
	__pop_heap_aux(first,last,value_type(first));
}

template <class RandomAccessIterator,class T>
inline void __pop_heap_aux(RandomAccessIterator first,RandomAccessIterator last,Distance*,T*)
{
     
	__pop_heap(first,last-1,last-1,T(*(last - 1)),diatance_type(first));
}

template <class RandomAccessIterator,class Distance,class T>
void __push_heap(RandomAccessIterator first,RandomAccessIterator last,RandomAccessIterator result,T value,Distance*)
{
     
	*result = *first;	//设定尾值为首值，客端稍后可以pop_back()将值取出
	__adjust_heap(first,Distance(0),Distance(last - first),value);
}

template <class RandomAccessIterator,class Distance,class T>
void __adjust_heap(RandomAccessIterator first,Distance holeIndex,Distance len,T value)
{
     
	Distance topIndex = holeIndex;
	Distance secondChild = 2 * 	holeIndex+2;	//右节点
	while(secondChild < len)
	{
     
		if(*(first + secondChild) < *(first +(secondChild -1)))
			secondChild --;
		*(first + holeIndex) = *(first + secondChild);
		holeIndex = secondChild;

		secondChild = 2*(secondChild+1);	//找出新洞节点的有子节点
	}
	if(secondChild == len)	//没有右子节点了
	{
     
		*(first + holeIndex) = *(first + secondChild -1);	//令左子值为键值
		holeIndex = secondChild - 1;	//再把洞的位置下移
	}
	__push_heap(first,holeIndex,topIndex,value);
}

sort_heap算法（思想简介）
不断对heap进行pop操作，便可达到排序效果。
这个图可以根据上面两张图自行脑补，算法也可以自行脑补。

heap迭代器
嘿嘿，那当然是没有迭代器了，所有元素都必须遵循特别的排列规则，又不提供遍历功能，要什么迭代器。

make_heap （制造heap）
这个算法就是用来将现有的一段数据转化成一个heap。

思想不多说，直接看代码：

template<class RandomAccessIterator>
template <class RandomAccessIterator>
inline void make_heap(RandomAccessIterator first,RandomAccessIterator last)
{
     
	__make_heap(first,last,distance_type(first),value_type(first));
}

//不允许指定比较方法
template <class RandomAccessIterator,class Distance,class T>
void __make_heap(RandomAccessIterator first,RandomAccessIterator last,Distance*,T*)
{
     
	if(last - first <2)	return;
	Distance len = last - first;
	Distance parent = (len - 1)/2;	//找出临时父节点
	while(true)	//尚未到达顶端，且父节点小于新值，这个循环将父值不断下调
	{
     
		__adjust_heap(first,parent,len,T(*(first+parent)));
		if(parent == 0)	return;	
		parent--;
	}
}