图像处理复习1——图像基础和空域增强

图像处理复习

---

CH2 图像基础

2.1 噪声

噪声定义为妨碍人们感觉器官对所接收的信源信息理解的因素，噪声有以下几个常见分类：

（1）按统计理论分类

• 平稳噪声：统计特性不随时间变化
• 非平稳噪声：统计特性随时间变化

（2）按频谱形状分类

• 白噪声:频谱均匀分布
• 三角噪声:频谱与频率平方成正比

（3）按幅度分布形状分类：高斯噪声、雷利噪声
（4）按噪声与信号关系分类：加性噪声、乘性噪声

处理噪声时往往假设噪声是加性噪声并且噪声和信号是相互统计独立的

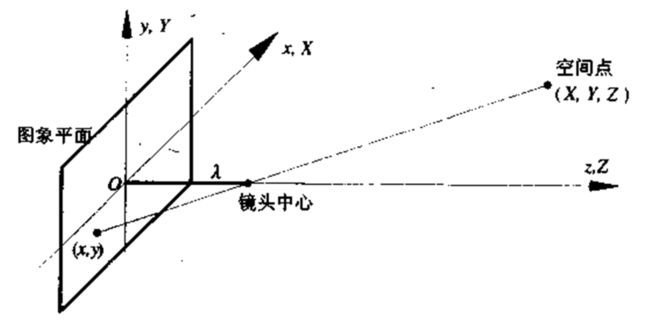
2.2 成像基础模型

假设投影成像有以下模型：

则由空间点 W=(X,Y,Z) 经 λ 的镜头透视后的摄影机坐标 C=(x,y,z) 和图像坐标 (x,y) 的由以下等量关系推导：

xλ=−XZ−λyλ=−YZ−λ

定义透视矩阵 p=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢10000100001−1λ0001⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥ ，那么有一般透视转换关系求法：

C=W⋅P=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢XYZ1⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⋅⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢10000100001−1λ0001⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢XYZλ−Zλ⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥

齐次化有：

C=1λ−Zλ⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢XYZλ−Zλ⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢Xλλ−ZYλλ−ZZλλ−Z1⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥

即摄影机坐标 (Xλλ−Z,Yλλ−Z,Zλλ−Z)T ，图像坐标 (Xλλ−Z,Yλλ−Z)T

求逆透视变换之用带入你透视变换矩阵 P′=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢100001000011λ0001⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥ 即可，过程推导略

2.3 像素联系

（1）邻域

一般关心三个像素邻域：

• 像素p的4邻域 N4(p)
• 像素p的4对角 ND(p)
• 像素p的8邻域 N8(p)=N4(p)⋃ND(p)

（2）连通性

连通性是定义在**连接相似准则**V，V是一个相似性取值集合，定义：

• 4-连接：若像素p和r在V中取值且r在 N4(p) 中
• 8-连接：若像素p和r在V中取值且r在 N8(p) 中
• m-连接：若像素p和r在V中取值且r要么在 N4(p) 中，要么在 ND(p) 中且 N4(p)⋂N4(r) 取值不能再V中出现

在上述定义基础上可以再定义通路的概念，

• 4-通路：像素p和r通过若干4-连接形成的通路，4-通路只能横纵走
• 8-通路：像素p和r通过若干8-连接形成的通路，8-通路即可横纵走又可斜向走
• 8-通路：像素p和r通过若干m-连接形成的通路，m-通路若即可以横纵到达又可以斜方向到达，必然选择横纵到达（选绕路的方案）

判断像素子集S、T在V上是否具有某连通，比较S、T的连接处两列像素是否具有某连通性即可

（3）距离

定义欧式距离 DE 为像素几何距离，街区距离 D4 为最短4-通路距离，棋盘距离 D8 为最短8-通路距离，还可以定义 Dm 为最短m-通路距离（意义？）

2.4 图像空间变换

空间点 (X,Y,Z) 变换到 (X′,Y′,Z′) 的变换矩阵为 M ，则有：

⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢X′Y′Z′1⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥=M⋅⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢XYZ1⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥

详细推导和引入齐次坐标系原因见图形学复习博客文章：http://blog.csdn.net/u014030117/article/details/46493115

平移变换矩阵：

T=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢100001000010X0Y0Z01⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥

尺度变换矩阵：

S=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢SX0000SY0000SZ00001⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥

二维绕原点旋转变换矩阵（顺时针旋转）：

R=⎡⎣⎢⎢⎢⎢⎢cosθ−sinθ0sinθcosθ0001⎤⎦⎥⎥⎥⎥⎥

注意：复合变换次序不可交换

---

CH3 图像空域增强

3.1 点运算

（1）灰度变换

灰度变换是根据灰度变换函数（原灰度到变换后灰度的映射关系，线性非线性均有）对每个像素原始灰度值进行变换的点运算，详见我另一篇博客：http://blog.csdn.net/u014030117/article/details/46367021

（2）直方图均衡化

直方图均衡主要用于增强动态范围偏小的图像的反差，其基本思想是把原始图像的直方图变换为均匀分布，从而增强灰度值的动态范围，以达到增强对比度的效果

直方图均衡化算法如下：

1. 归一化灰度频数直方图，得到频率直方图sk
2. 用sk计算频率累计直方图tk
3. tk做取整扩展：tk = int[(L - 1) * tk + 0.5]，将直方图灰度映射尽量满整个灰度取值空间L
4. 确定变换映射关系k->tk
5. 根据映射关系变换图像灰度值

非理想均衡化原因：

从映射关系：数字图像是离散的，直方图均衡化方法是一对一或者多对一的映射关系，即原图像的某一灰度级或某几个灰度级只能映射为均衡化图像的一个灰度级，因此不能实现理想的均衡
从映射计算：均值化算法中运用了取整运算，而不是离散值的完全均衡化

理想均衡化：实现灰度级多对多的映射关系

1道习题：已用直方图均衡化技术对一幅数字图像进行了增强，试证明再用这个方法对所得结果增强并不会改变其结果：

答：从原理上分析，直方图均衡化所用的变换函数为原始图像的累积直方图，均衡化后得到的增强图像的累积直方图除有些项合并外，其余项与原始图像的累积直方图相同。如果再次均衡化，所用的变换函数即为均衡化后得到的增强图像的累积直方图(并不会有新的合并项)，所以不会改变其结果
注：形式化证明有点复杂，我没证出来TAT

（3）直方图规定化

直方图规定化是把直方图映射变换到指定的直方图形状

规定化算法如下：

1. 归一化原始图像灰度频数直方图，得到频率直方图
2. 计算原始图像频率累计直方图
3. 计算规定直方图的累积直方图
4. 对原始图像累计直方图的每个值，确定一个距该值最接近的规定直方图的频率不为0的灰度级的累积量，作为映射；确定所有SML映射关系
5. 根据映射关系变换图像灰度值

3.2 领域处理

领域处理分为平滑和锐化，详见我其他两篇博客博客：

• 空域平滑滤波：http://blog.csdn.net/u014030117/article/details/46369671
• 空域锐化滤波：http://blog.csdn.net/u014030117/article/details/46383659

3.3 局部增强

图像局部增强一般采取的方法是对图像分区，在各个局部分区中做局部增强（如局部直方图均衡化等）