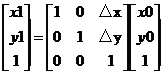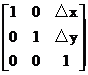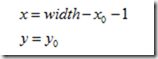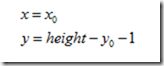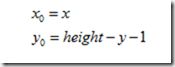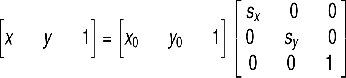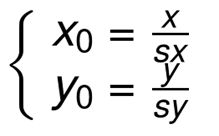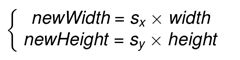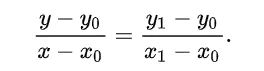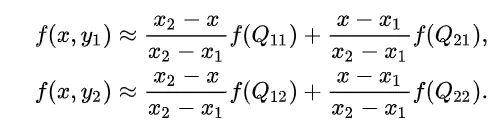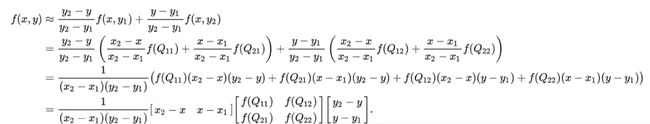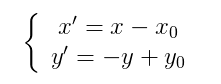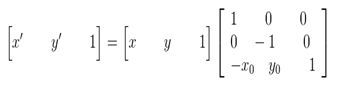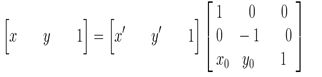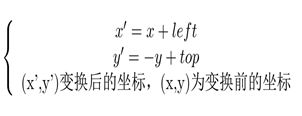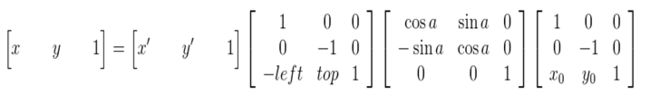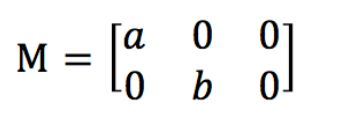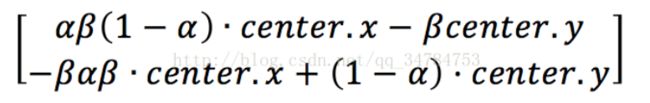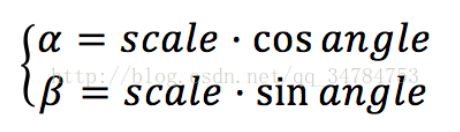matlab 向前映射,十、图像的几何变换——平移、镜像、缩放、旋转、仿射变换 OpenCV2:图像的几何变换,平移、镜像、缩放、旋转(1) OpenCV2:图像的几何变换,平移、镜像、缩放、旋转(2...
1.几何变换的基本概念
图像几何变换又称为图像空间变换,它将一副图像中的坐标位置映射到另外一幅图像中的新坐标位置。咱们学习几何变换就是肯定这种空间映射关系,以及映射过程当中的变化参数。图像的几何变换改变了像素的空间位置,创建一种原图像像素与变换后图像像素之间的映射关系,经过这种映射关系可以实现下面两种计算:html
原图像任意像素计算该像素在变换后图像的坐标位置
变换后图像的任意像素在原图像的坐标位置
对于第一种计算,只要给出原图像上的任意像素坐标,都能经过对应的映射关系得到到该像素在变换后图像的坐标位置。将这种输入图像坐标映射到输出的过程称为“向前映射”。反过来,知道任意变换后图像上的像素坐标,计算其在原图像的像素坐标,将输出图像映射到输入的过程称为“向后映射”。可是,在使用向前映射处理几何变换时却有一些不足,一般会产生两个问题:映射不彻底,映射重叠ios
映射不彻底
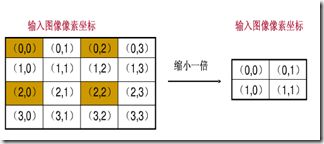
输入图像的像素总数小于输出图像,这样输出图像中的一些像素找不到在原图像中的映射。
上图只有(0,0),(0,2),(2,0),(2,2)四个坐标根据映射关系在原图像中找到了相对应的像素,其他的12个坐标没有有效值。
映射重叠
根据映射关系,输入图像的多个像素映射到输出图像的同一个像素上。
上图左上角的四个像素(0,0),(0,1),(1,0),(1,1)都会映射到输出图像的(0,0)上,那么(0,0)究竟取那个像素值呢?
要解决上述两个问题可使用“向后映射”,使用输出图像的坐标反过来推算改坐标对应于原图像中的坐标位置。这样,输出图像的每一个像素均可以经过映射关系在原图像找到惟一对应的像素,而不会出现映射不彻底和映射重叠。因此,通常使用向后映射来处理图像的几何变换。从上面也能够看出,向前映射之因此会出现问题,主要是因为图像像素的总数发生了变化,也就是图像的大小改变了。在一些图像大小不会发生变化的变换中,向前映射仍是颇有效的。web
2.图像平移
图像的平移变换就是将图像全部的像素坐标分别加上指定的水平偏移量和垂直偏移量。平移变换根据是否改变图像大小分为两种,直接丢弃或者经过加目标图像尺寸的方法使图像可以包含这些点。算法
2.1平移变换原理
假设原来的像素的位置坐标为(x0,y0),通过平移量(△x,△y)后,坐标变为(x1,y1),以下所示:函数
用数学式子表示能够表示为:post
x1 = x0 + △x,性能
y1 = y0 + △y;学习
用矩阵表示为:优化
原本使用二维矩阵就能够了的,可是为了适应像素、拓展适应性,这里使用三维的向量。ui
式子中,矩阵:
称为平移变换矩阵(因子),△x和△y为平移量。
2.2 基于OpenCV的实现
图像的平移变换实现仍是很简单的,这里再也不赘述.
平移后图像的大小不变
![]()
void GeometricTrans::translateTransform(cv::Mat const& src, cv::Mat& dst, int dx, int dy)
{
CV_Assert(src.depth() == CV_8U);
const int rows = src.rows;
const int cols = src.cols;
dst.create(rows, cols, src.type());
Vec3b *p;
for (int i = 0; i < rows; i++)
{
p = dst.ptr(i);
for (int j = 0; j < cols; j++)
{
//平移后坐标映射到原图像
int x = j - dx;
int y = i - dy;
//保证映射后的坐标在原图像范围内
if (x >= 0 && y >= 0 && x < cols && y < rows)
p[j] = src.ptr(y)[x];
}
}
}
![]()
平移后图像的大小变化
![]()
void GeometricTrans::translateTransformSize(cv::Mat const& src, cv::Mat& dst, int dx, int dy)
{
CV_Assert(src.depth() == CV_8U);
const int rows = src.rows + abs(dy); //输出图像的大小
const int cols = src.cols + abs(dx);
dst.create(rows, cols, src.type());
Vec3b *p;
for (int i = 0; i < rows; i++)
{
p = dst.ptr(i);
for (int j = 0; j < cols; j++)
{
int x = j - dx;
int y = i - dy;
if (x >= 0 && y >= 0 && x < src.cols && y < src.rows)
p[j] = src.ptr(y)[x];
}
}
}
![]()
ps:这里图像变换的代码以三通道图像为例,单通道的于此相似,代码中没有作处理。
示例:
#include "stdafx.h"
#include
#include
#include
#include
using namespace std;
using namespace cv;
void translateTransform(cv::Mat const& src, cv::Mat& dst, int dx, int dy)//平移后大小不变
{
CV_Assert(src.depth() == CV_8U);
const int rows = src.rows;
const int cols = src.cols;
dst.create(rows, cols, src.type());
Vec3b *p;
for (int i = 0; i < rows; i++)
{
p = dst.ptr(i);
for (int j = 0; j < cols; j++)
{
//平移后坐标映射到原图像
int x = j - dx;
int y = i - dy;
//保证映射后的坐标在原图像范围内
if (x >= 0 && y >= 0 && x < cols && y < rows)
p[j] = src.ptr(y)[x];
}
}
}
void translateTransformSize(cv::Mat const& src, cv::Mat& dst, int dx, int dy)//平移后大小变化
{
CV_Assert(src.depth() == CV_8U);
const int rows = src.rows + abs(dy); //输出图像的大小
const int cols = src.cols + abs(dx);
dst.create(rows, cols, src.type());
Vec3b *p;
for (int i = 0; i < rows; i++)
{
p = dst.ptr(i);
for (int j = 0; j < cols; j++)
{
int x = j - dx;
int y = i - dy;
if (x >= 0 && y >= 0 && x < src.cols && y < src.rows)
p[j] = src.ptr(y)[x];
}
}
}
int main()
{
Mat srcImage, dstImage0, dstImage1, dstImage2;
int xOffset, yOffset;//x和y方向的平移量
srcImage = imread("111.jpg");
if (!srcImage.data)
{
cout << "读入图片错误!" << endl;
return -1;
}
cout << "请输入x方向和y方向的平移量:";
cin >> xOffset >> yOffset;
int rowNumber = srcImage.rows;
int colNumber = srcImage.cols;
translateTransform(srcImage, dstImage0, xOffset, yOffset);
translateTransformSize(srcImage, dstImage1, xOffset, yOffset);
imshow("原图像", srcImage);
imshow("不丢弃平移后的图像", dstImage0);
imshow("丢弃平移后的图像", dstImage1);
waitKey();
return 0;
}
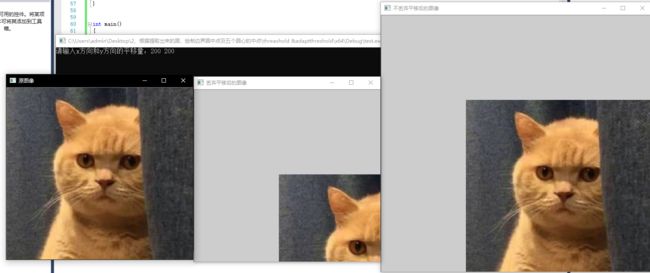
在输入框输入200,200后结果为
3.图像的镜像变换
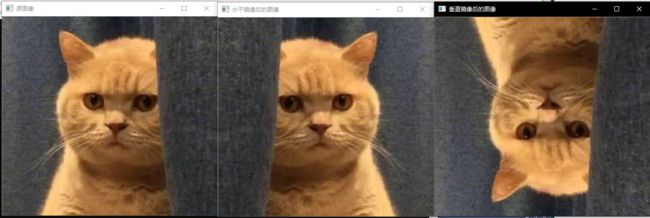
图像的镜像变换分为两种:水平镜像和垂直镜像。水平镜像以图像垂直中线为轴,将图像的像素进行对换,也就是将图像的左半部和右半部对调。垂直镜像则是以图像的水平中线为轴,将图像的上半部分和下班部分对调。
3.1变换原理
水平变换
其逆变换为
2.垂直镜像变换
其逆变换为
3.2基于OpenCV的实现
水平镜像的实现
![]()
void GeometricTrans::hMirrorTrans(const Mat &src, Mat &dst)
{
CV_Assert(src.depth() == CV_8U);
dst.create(src.rows, src.cols, src.type());
int rows = src.rows;
int cols = src.cols;
switch (src.channels())
{
case 1:
const uchar *origal;
uchar *p;
for (int i = 0; i < rows; i++){
origal = src.ptr(i);
p = dst.ptr(i);
for (int j = 0; j < cols; j++){
p[j] = origal[cols - 1 - j];
}
}
break;
case 3:
const Vec3b *origal3;
Vec3b *p3;
for (int i = 0; i < rows; i++) {
origal3 = src.ptr(i);
p3 = dst.ptr(i);
for(int j = 0; j < cols; j++){
p3[j] = origal3[cols - 1 - j];
}
}
break;
default:
break;
}
}
![]()
分别对三通道图像和单通道图像作了处理,因为比较相似之后的代码只处理三通道图像,再也不作特别说明。
在水平镜像变换时,遍历了整个图像,而后根据映射关系对每一个像素都作了处理。实际上,水平镜像变换就是将图像坐标的列换到右边,右边的列换到左边,是能够以列为单位作变换的。一样垂直镜像变换也如此,能够以行为单位进行变换。
垂直镜像变换
![]()
void GeometricTrans::vMirrorTrans(const Mat &src, Mat &dst)
{
CV_Assert(src.depth() == CV_8U);
dst.create(src.rows, src.cols, src.type());
int rows = src.rows;
for (int i = 0; i < rows; i++)
src.row(rows - i - 1).copyTo(dst.row(i));
}
![]()
上面一行代码是变换的核心代码,从原图像中取出第i行,并将其复制到目标图像。
示例:
#include "stdafx.h"
#include
#include
#include
#include
using namespace std;
using namespace cv;
void hMirrorTrans(const Mat &src, Mat &dst)
{
CV_Assert(src.depth() == CV_8U);
dst.create(src.rows, src.cols, src.type());
int rows = src.rows;
int cols = src.cols;
switch (src.channels())
{
case 1:
const uchar *origal;
uchar *p;
for (int i = 0; i < rows; i++) {
origal = src.ptr(i);
p = dst.ptr(i);
for (int j = 0; j < cols; j++) {
p[j] = origal[cols - 1 - j];
}
}
break;
case 3:
const Vec3b *origal3;
Vec3b *p3;
for (int i = 0; i < rows; i++) {
origal3 = src.ptr(i);
p3 = dst.ptr(i);
for (int j = 0; j < cols; j++) {
p3[j] = origal3[cols - 1 - j];
}
}
break;
default:
break;
}
}
void vMirrorTrans(const Mat &src, Mat &dst)
{
CV_Assert(src.depth() == CV_8U);
dst.create(src.rows, src.cols, src.type());
int rows = src.rows;
for (int i = 0; i < rows; i++)
src.row(rows - i - 1).copyTo(dst.row(i));
}
int main()
{
Mat srcImage, dstImage, dstImage1;;
srcImage = imread("111.jpg");
if (!srcImage.data)
{
cout << "读入图片错误!" << endl;
return -1;
}
hMirrorTrans(srcImage, dstImage);
vMirrorTrans(srcImage, dstImage1);
imshow("原图像", srcImage);
imshow("水平镜像后的图像", dstImage);
imshow("垂直镜像后的图像", dstImage1);
waitKey();
return 0;
}
程序运行结果以下:
3.图像缩放
图像的缩放指的是将图像的尺寸变小或变大的过程,也就是减小或增长原图像数据的像素个数。简单来讲,就是经过增长或删除像素点来改变图像的尺寸。当图像缩小时,图像会变得更加清晰,当图像放大时,图像的质量会有所降低,所以须要进行插值处理。
3.1 缩放原理
设水平缩放系数为sx,垂直缩放系数为sy,(x0,y0)为缩放前坐标,(x,y)为缩放后坐标,其缩放的坐标映射关系: ![]()
矩阵表示的形式为:
这是向前映射,在缩放的过程改变了图像的大小,使用向前映射会出现映射重叠和映射不彻底的问题,因此这里更关心的是向后映射,也就是输出图像经过向后映射关系找到其在原图像中对应的像素。
向后映射关系:
3.2基于OpenCV的缩放实现
在用前一篇文章讲到利用resize函数的进行图像的缩放操做,函数的原型为:
resize( InputArray src, OutputArray dst,Size dsize, double fx=0, double fy=0,int interpolation=INTER_LINEAR );
这里固然能够用resize进行缩放,可是为了更好的理解缩放原理,这里利用向后映射进行图像缩放,过程为:
首先进行计算新图像的大小,在这里设newWidth和newHeight分别表示新图像的宽度和高度,width和height表示原始图像的宽度和高度,
在图像缩放的时首先须要计算缩放后图像的大小,设newWidth,newHeight为缩放后的图像的宽和高,width,height为原图像的宽度和高度,那么有:
而后再进行枚举新图像每一个像素的坐标,经过向后映射计算出该像素映射在原始图像的坐标位置,再进行获取该像素的值。
根据上面公式可知,缩放后图像的宽和高用原图像宽和高和缩放因子相乘便可。
int rows = static_cast(src.rows * xRatio + 0.5);
int cols = static_cast(src.cols * yRatio + 0.5);
须要注意的是,在进行后向映射的过程当中可能会产生浮点数坐标,可是数字图像是以离散型整数存储数据的,因此没法获得浮点数坐标对应的像素值,这里就须要进行插值算法计算坐标是浮点型的像素值。这里使用最邻近插值和双线性插值来处理。
3.3插值算法
0、什么叫插值
数学的数值分析领域中,内插或称插值(英语:interpolation)是一种经过已知的、离散的数据点,在范围内推求新数据点的过程或方法。
 一组离散数据点在一个外延的插值。曲线中实际已知数据点是红色的;链接它们的蓝色曲线即为插值。在一个函数里面,自变量是离散有间隔的,插值就是往自变量的间隔之间插入新的自变量,而后求解新的自变量函数值。
一组离散数据点在一个外延的插值。曲线中实际已知数据点是红色的;链接它们的蓝色曲线即为插值。在一个函数里面,自变量是离散有间隔的,插值就是往自变量的间隔之间插入新的自变量,而后求解新的自变量函数值。
常见的插值算法有最邻近插值法、双线性插值法,双三次插值法等。双三次插值法因为计算量较大,这里不作详细讲解,有兴趣的能够看参考资料中的实现opencv中经常使用的三种插值算法
一、最邻近插值
最近邻域是三种插值之中最简单的一种,原理就是选取距离插入的像素点(x+u, y+v)【注:x,y为整数, u,v为小数】最近的一个像素点,用它的像素点的灰度值代替插入的像素点。
void nearestIntertoplation(cv::Mat& src, cv::Mat& dst, const int rows, const int cols)
{
//比例尺
const double scale_row = static_cast(src.rows) / rows;
const double scale_col = static_cast(src.rows) / cols;
//扩展src到dst
dst = cv::Mat(rows, cols, src.type());
assert(src.channels() == 1 && dst.channels() == 1);
for (int i = 0; i < rows; ++i)//dst的行
for (int j = 0; j < cols; ++j)//dst的列
{
//求插值的四个点
double y = (i + 0.5) * scale_row + 0.5;
double x = (j + 0.5) * scale_col + 0.5;
int x1 = static_cast(x);//col对应x
if (x1 >= (src.cols - 2)) x1 = src.cols - 2;//防止越界
int x2 = x1 + 1;
int y1 = static_cast(y);//row对应y
if (y1 >= (src.rows - 2)) y1 = src.rows - 2;
int y2 = y1 + 1;
//根据目标图像的像素点(浮点坐标)找到原始图像中的4个像素点,取距离该像素点最近的一个原始像素值做为该点的值。
assert(0 < x2 && x2 < src.cols && 0 < y2 && y2 < src.rows);
std::vector dist(4);
dist[0] = distance(x, y, x1, y1);
dist[1] = distance(x, y, x2, y1);
dist[2] = distance(x, y, x1, y2);
dist[3] = distance(x, y, x2, y2);
int min_val = dist[0];
int min_index = 0;
for (int i = 1; i < dist.size(); ++i)
if (min_val > dist[i])
{
min_val = dist[i];
min_index = i;
}
switch (min_index)
{
case 0:
dst.at(i, j) = src.at(y1, x1);
break;
case 1:
dst.at(i, j) = src.at(y1, x2);
break;
case 2:
dst.at(i, j) = src.at(y2, x1);
break;
case 3:
dst.at(i, j) = src.at(y2, x2);
break;
default:
assert(false);
}
}
}
double distance(const double x1, const double y1, const double x2, const double y2)//两点之间距离,这里用欧式距离
{
return (x1 - x2)*(x1 - x2) + (y1 - y2)*(y1 - y2);//只需比较大小,返回距离平方便可
}
最邻近插值只须要对浮点坐标“四舍五入”运算。可是在四舍五入的时候有可能使获得的结果超过原图像的边界(只会比边界大1),因此要进行下修正。
最邻近插值几乎没有多余的运算,速度至关快。可是这种邻近取值的方法是很粗糙的,会形成图像的马赛克、锯齿等现象。
双线性插值
双线性插值的精度要比最邻近插值好不少,相对的其计算量也要大的多。双线性插值的主要思想是计算出浮点坐标像素近似值。那么要如何计算浮点坐标的近似值呢。一个浮点坐标一定会被四个整数坐标所包围,将这个四个整数坐标的像素值按照必定的比例混合就能够求出浮点坐标的像素值。混合比例为距离浮点坐标的距离。 双线性插值使用浮点坐标周围四个像素的值按照必定的比例混合近似获得浮点坐标的像素值。
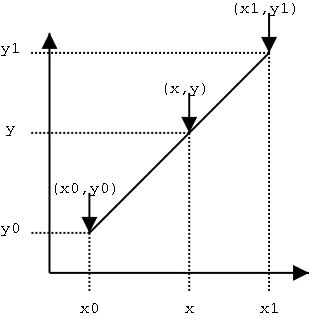
首先看看线性插值
下面经过一个例子进行理解:
假设要求坐标为(2.4,3)的像素值P,该点在(2,3)和(3,3)之间,以下图
u和v分别是距离浮点坐标最近两个整数坐标像素在浮点坐标像素所占的比例
P(2.4,3) = u * P(2,3) + v * P(3,3),混合的比例是以距离为依据的,那么u = 0.4,v = 0.6。
接下来看看二维中的双线性插值
首先在x方向上面线性插值,获得R二、R1
而后以R2,R1在y方向上面再次线性插值
一样,经过一个实例进行理解
进行双线性插值运算
(2.4,3)的像素值 F1 = m * T1 + (1 – m) * T2
(2.4,4)的像素值 F2 = m * T3 + (1 – m ) * T4
(2.4,3.5)的像素值 F = n * F1 + (1 – n) * F2
这样就能够求得浮点坐标(2.4,3.5)的像素值了。
求浮点坐标像素F,设该浮点坐标周围的4个像素值分别为T1,T2,T3,T4,而且浮点坐标距离其左上角的横坐标的差为m,纵坐标的差为n。 故有
F1 = m * T1 + (1 – m) * T2
F2 = m * T3 + (1 – m) *T4
F = n * F1 + (1 – n) * F2
上面就是双线性插值的基本公式,能够看出,计算每一个像素像素值须要进行6次浮点运算。并且,因为浮点坐标有4个坐标近似求得,若是这个四个坐标的像素值差异较大,插值后,会使得图像在颜色分界较为明显的地方变得比较模糊。
OpenCV实现以下:
void bilinearIntertpolatioin(cv::Mat& src, cv::Mat& dst, const int rows, const int cols)
{
//比例尺
const double scale_row = static_cast(src.rows) / rows;
const double scale_col = static_cast(src.rows) / cols;
//扩展src到dst
dst = cv::Mat(rows, cols, src.type());
assert(src.channels() == 1 && dst.channels() == 1);
for(int i = 0; i < rows; ++i)//dst的行
for (int j = 0; j < cols; ++j)//dst的列
{
//求插值的四个点
double y = (i + 0.5) * scale_row + 0.5;
double x = (j + 0.5) * scale_col + 0.5;
int x1 = static_cast(x);//col对应x
if (x1 >= (src.cols - 2)) x1 = src.cols - 2;//防止越界
int x2 = x1 + 1;
int y1 = static_cast(y);//row对应y
if (y1 >= (src.rows - 2)) y1 = src.rows - 2;
int y2 = y1 + 1;
assert(0 < x2 && x2 < src.cols && 0 < y2 && y2 < src.rows);
//插值公式,参考维基百科矩阵相乘的公式https://zh.wikipedia.org/wiki/%E5%8F%8C%E7%BA%BF%E6%80%A7%E6%8F%92%E5%80%BC
cv::Matx12d matx = { x2 - x, x - x1 };
cv::Matx22d matf = { static_cast(src.at(y1, x1)), static_cast(src.at(y2, x1)),
static_cast(src.at(y1, x2)), static_cast(src.at(y2, x2)) };
cv::Matx21d maty = {
y2 - y,
y - y1
};
auto val = (matx * matf * maty);
dst.at(i, j) = val(0,0);
}
}
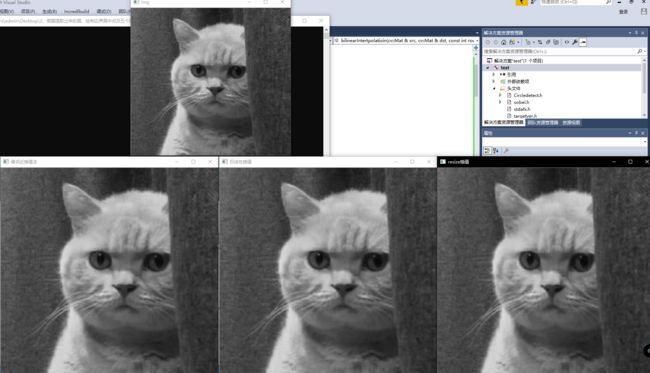
3.3示例
这里用resize、最近邻域插值和双线性插值(这里给出的两种实现都是基于灰度图的)
#include "stdafx.h"
#include
#include
#include
double distance(const double x1, const double y1, const double x2, const double y2)//两点之间距离,这里用欧式距离
{
return (x1 - x2)*(x1 - x2) + (y1 - y2)*(y1 - y2);//只需比较大小,返回距离平方便可
}
void nearestIntertoplation(cv::Mat& src, cv::Mat& dst, const int rows, const int cols)
{
//比例尺
const double scale_row = static_cast(src.rows) / rows;
const double scale_col = static_cast(src.rows) / cols;
//扩展src到dst
dst = cv::Mat(rows, cols, src.type());
assert(src.channels() == 1 && dst.channels() == 1);
for (int i = 0; i < rows; ++i)//dst的行
for (int j = 0; j < cols; ++j)//dst的列
{
//求插值的四个点
double y = (i + 0.5) * scale_row + 0.5;
double x = (j + 0.5) * scale_col + 0.5;
int x1 = static_cast(x);//col对应x
if (x1 >= (src.cols - 2)) x1 = src.cols - 2;//防止越界
int x2 = x1 + 1;
int y1 = static_cast(y);//row对应y
if (y1 >= (src.rows - 2)) y1 = src.rows - 2;
int y2 = y1 + 1;
//根据目标图像的像素点(浮点坐标)找到原始图像中的4个像素点,取距离该像素点最近的一个原始像素值做为该点的值。
assert(0 < x2 && x2 < src.cols && 0 < y2 && y2 < src.rows);
std::vector dist(4);
dist[0] = distance(x, y, x1, y1);
dist[1] = distance(x, y, x2, y1);
dist[2] = distance(x, y, x1, y2);
dist[3] = distance(x, y, x2, y2);
int min_val = dist[0];
int min_index = 0;
for (int i = 1; i < dist.size(); ++i)
if (min_val > dist[i])
{
min_val = dist[i];
min_index = i;
}
switch (min_index)
{
case 0:
dst.at(i, j) = src.at(y1, x1);
break;
case 1:
dst.at(i, j) = src.at(y1, x2);
break;
case 2:
dst.at(i, j) = src.at(y2, x1);
break;
case 3:
dst.at(i, j) = src.at(y2, x2);
break;
default:
assert(false);
}
}
}
void bilinearIntertpolatioin(cv::Mat& src, cv::Mat& dst, const int rows, const int cols)
{
//比例尺
const double scale_row = static_cast(src.rows) / rows;
const double scale_col = static_cast(src.rows) / cols;
//扩展src到dst
dst = cv::Mat(rows, cols, src.type());
assert(src.channels() == 1 && dst.channels() == 1);
for (int i = 0; i < rows; ++i)//dst的行
for (int j = 0; j < cols; ++j)//dst的列
{
//求插值的四个点
double y = (i + 0.5) * scale_row + 0.5;
double x = (j + 0.5) * scale_col + 0.5;
int x1 = static_cast(x);//col对应x
if (x1 >= (src.cols - 2)) x1 = src.cols - 2;//防止越界
int x2 = x1 + 1;
int y1 = static_cast(y);//row对应y
if (y1 >= (src.rows - 2)) y1 = src.rows - 2;
int y2 = y1 + 1;
assert(0 < x2 && x2 < src.cols && 0 < y2 && y2 < src.rows);
//插值公式,参考维基百科矩阵相乘的公式https://zh.wikipedia.org/wiki/%E5%8F%8C%E7%BA%BF%E6%80%A7%E6%8F%92%E5%80%BC
cv::Matx12d matx = { x2 - x, x - x1 };
cv::Matx22d matf = { static_cast(src.at(y1, x1)), static_cast(src.at(y2, x1)),
static_cast(src.at(y1, x2)), static_cast(src.at(y2, x2)) };
cv::Matx21d maty = {
y2 - y,
y - y1
};
auto val = (matx * matf * maty);
dst.at(i, j) = val(0, 0);
}
}
int main()
{
cv::Mat img = cv::imread("111.jpg", 0);
if (img.empty()) return -1;
cv::Mat dst,dst1,dst2;
nearestIntertoplation(img, dst, 600, 600);
bilinearIntertpolatioin(img, dst1, 600, 600);
resize(img, dst2, dst1.size());
cv::imshow("img", img);
cv::imshow("最邻近插值法", dst);
cv::imshow("双线性插值", dst1);
cv::imshow("resize插值", dst2);
cv::waitKey(0);
return 0;
return 0;
}//main
4.图像旋转
4.1旋转原理
图像的旋转就是让图像按照某一点旋转指定的角度。图像旋转后不会变形,可是其垂直对称抽和水平对称轴都会发生改变,旋转后图像的坐标和原图像坐标之间的关系已不能经过简单的加减乘法获得,而须要经过一系列的复杂运算。并且图像在旋转后其宽度和高度都会发生变化,其坐标原点会发生变化。
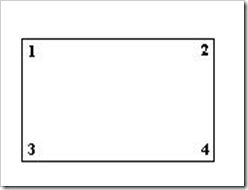
图像所用的坐标系不是经常使用的笛卡尔,其左上角是其坐标原点,X轴沿着水平方向向右,Y轴沿着竖直方向向下。而在旋转的过程通常使用旋转中心为坐标原点的笛卡尔坐标系,因此图像旋转的第一步就是坐标系的变换。设旋转中心为(x0,y0),(x’,y’)是旋转后的坐标,(x,y)是旋转后的坐标,则坐标变换以下:
矩阵表示为:
在最终的实现中,经常使用到的是有缩放后的图像经过映射关系找到其坐标在原图像中的相应位置,这就须要上述映射的逆变换
坐标系变换到以旋转中心为原点后,接下来就要对图像的坐标进行变换。
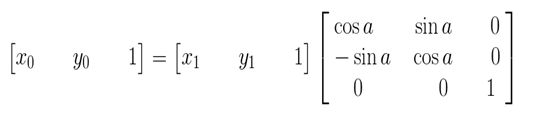
上图所示,将坐标(x0,y0)顺时针方向旋转a,获得(x1,y1)。
旋转前有:
旋转a后有:
矩阵的表示形式:
其逆变换:
因为在旋转的时候是以旋转中心为坐标原点的,旋转结束后还须要将坐标原点移到图像左上角,也就是还要进行一次变换。这里须要注意的是,旋转中心的坐标(x0,y0)实在以原图像的左上角为坐标原点的坐标系中获得,而在旋转后因为图像的宽和高发生了变化,也就致使了旋转后图像的坐标原点和旋转前的发生了变换。
上边两图,能够清晰的看到,旋转先后图像的左上角,也就是坐标原点发生了变换。
在求图像旋转后左上角的坐标前,先来看看旋转后图像的宽和高。从上图能够看出,旋转后图像的宽和高与原图像的四个角旋转后的位置有关。
设top为旋转后最高点的纵坐标,down为旋转后最低点的纵坐标,left为旋转后最左边点的横坐标,right为旋转后最右边点的横坐标。
旋转后的宽和高为newWidth,newHeight,则可获得下面的关系:
也就很容易的得出旋转后图像左上角坐标(left,top)(以旋转中心为原点的坐标系)
故在旋转完成后要将坐标系转换为以图像的左上角为坐标原点,可由下面变换关系获得:
矩阵表示:
其逆变换:
综合以上,也就是说原图像的像素坐标要通过三次的坐标变换:
将坐标原点由图像的左上角变换到旋转中心
以旋转中心为原点,图像旋转角度a
旋转结束后,将坐标原点变换到旋转后图像的左上角
能够获得下面的旋转公式:(x’,y’)旋转后的坐标,(x,y)原坐标,(x0,y0)旋转中心,a旋转的角度(顺时针)
这种由输入图像经过映射获得输出图像的坐标,是向前映射。经常使用的向后映射是其逆运算
4.2基于OpenCV的实现
获得了上述的旋转公式,实现起来就不是很困难了.
Mat nearestNeighRotate(cv::Mat img, float angle)
{
int len = (int)(sqrtf(pow(img.rows, 2) + pow(img.cols, 2)) + 0.5);
Mat retMat = Mat::zeros(len, len, CV_8UC3);
float anglePI = angle * CV_PI / 180;
int xSm, ySm;
for (int i = 0; i < retMat.rows; i++)
for (int j = 0; j < retMat.cols; j++)
{
xSm = (int)((i - retMat.rows / 2)*cos(anglePI) - (j - retMat.cols / 2)*sin(anglePI) + 0.5);
ySm = (int)((i - retMat.rows / 2)*sin(anglePI) + (j - retMat.cols / 2)*cos(anglePI) + 0.5);
xSm += img.rows / 2;
ySm += img.cols / 2;
if (xSm >= img.rows || ySm >= img.cols || xSm <= 0 || ySm <= 0) {
retMat.at(i, j) = Vec3b(0, 0);
}
else {
retMat.at(i, j) = img.at(xSm, ySm);
}
}
return retMat;
}
示例
#include "stdafx.h"
#include
#include
#include
using namespace std;
using namespace cv;
Mat nearestNeighRotate(cv::Mat img, float angle)
{
int len = (int)(sqrtf(pow(img.rows, 2) + pow(img.cols, 2)) + 0.5);
Mat retMat = Mat::zeros(len, len, CV_8UC3);
float anglePI = angle * CV_PI / 180;
int xSm, ySm;
for (int i = 0; i < retMat.rows; i++)
for (int j = 0; j < retMat.cols; j++)
{
xSm = (int)((i - retMat.rows / 2)*cos(anglePI) - (j - retMat.cols / 2)*sin(anglePI) + 0.5);
ySm = (int)((i - retMat.rows / 2)*sin(anglePI) + (j - retMat.cols / 2)*cos(anglePI) + 0.5);
xSm += img.rows / 2;
ySm += img.cols / 2;
if (xSm >= img.rows || ySm >= img.cols || xSm <= 0 || ySm <= 0) {
retMat.at(i, j) = Vec3b(0, 0);
}
else {
retMat.at(i, j) = img.at(xSm, ySm);
}
}
return retMat;
}
int main()
{
Mat img = imread("111.jpg");
Mat retImg;
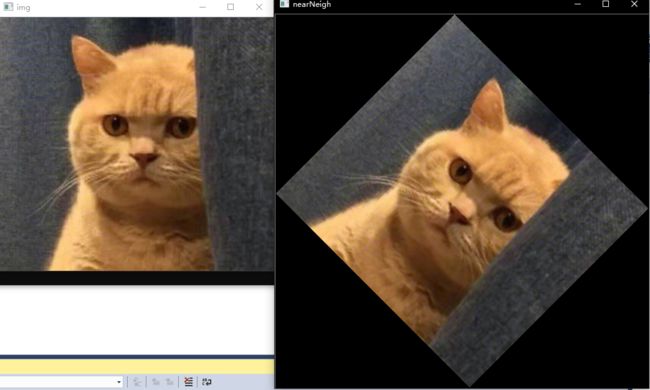
retImg = nearestNeighRotate(img, 45.f);
imshow("img", img);
imshow("nearNeigh", retImg);
waitKey();
cvDestroyAllWindows();
return 0;
}
运行结果以下:
2.3 仿射变换
咱们除了本身写相关函数外,OpenCV还提供了对应的仿射变换的API接口函数warpAffine,仿射变换是指在向量空间中进行一次线性变换(乘以一个矩阵)并加上一个平移(加上一个向量),变换为另外一个向量空间的过程。在有限维的状况下,每一个仿射变换能够由一个矩阵A和一个向量b给出,它能够写做A和一个附加的列b。一个仿射变换对应于一个矩阵和一个向量的乘法,而仿射变换的复合对应于普通的矩阵乘法,只要加入一个额外的行到矩阵的底下,这一行所有是0除了最右边是一个1,而列向量的底下要加上一个1.
实际上,仿射变换表明的是两幅图之间的关系,咱们一般使用2x3矩阵来表示仿射变换以下:
考虑到咱们要使用矩阵A和B对二维向量
![]()
获得以下结果:
应用图像仿射变换矩阵,能够获得大部分的几何变换结果,例如以前提到的平移变换等,根据平移变换矩阵能够很容易的获得实现平移功能的仿射变换矩阵,以下所示:
对于图像缩放来讲,设水平方向的缩放因子为a,垂直方向缩放因子为b,则用仿射矩阵实现图缩放功能的仿射矩阵为:
而对于图像旋转来讲,设旋转角度为θ,利用仿射变换实现图像旋转操做的仿射矩阵为:
而对于较为特殊的斜切变换,一样的,设斜切的角度为θ,则仿射矩阵为:
须要注意的是,在OpenCV中使用仿射变换函数时,一般会先计算一个仿射变换矩阵,以此来得到仿射变换矩阵,为了实现这个功能,经常使用getRotationMatrix2D()函数用来计算二维旋转矩阵,这个变换会将旋转中心映射到它自身。这里给出它的函数声明:
Mat getRotationMatrix2D( Point2f center, double angle, double scale );
这个函数中有三个参数,第一个参数是Point2f类型的center,也就是原图像的旋转中心;第二个参数是double 类型的angle,也就是咱们说的旋转角度,值得一提的是,当angle的值为正时,表示的是逆时针旋转,当angle的值为负时,表示的是顺时针旋转。第三个参数scale表示的是缩放系数,在这个函数计算的是下面这个矩阵:
其中
获得仿射变换矩阵后,便可调用仿射函数,仿射映射函数声明为:
voidcv::warpAffine (
InputArray src,
OutputArray dst,
InputArray M,
Size dsize,
int flags =INTER_LINEAR,
int borderMode =BORDER_CONSTANT,
const Scalar & borderValue =Scalar()
)
参数解释
. src: 输入图像
. dst: 输出图像,尺寸由dsize指定,图像类型与原图像一致
. M: 2X3的变换矩阵
. dsize: 指定图像输出尺寸
. flags: 插值算法标识符,有默认值INTER_LINEAR,若是插值算法为WARP_INVERSE_MAP, warpAffine函数使用以下矩阵进行图像转换
经常使用的插值算法以下:
. borderMode: 边界像素模式,有默认值BORDER_CONSTANT
. borderValue: 边界取值,有默认值Scalar()即0
示例:
#include "stdafx.h"
#include
#include
#include
#include
#include
#include
#include
using namespace std;
using namespace cv;
int main()
{
Mat srcImage, dstImage;
srcImage = imread("111.jpg");
if (!srcImage.data)
{
cout << "读入图片有误!" << endl;
return -1;
}
imshow("原图像", srcImage);
dstImage.create(srcImage.size(), srcImage.type());
double degree;
cout << "请输入旋转角度:";
cin >> degree;
double a = sin(degree * CV_PI / 180);
double b = cos(degree * CV_PI / 180);
int width = srcImage.cols;
int height = srcImage.rows;
int rotate_width = int(height * fabs(a) + width * fabs(b));
int rotate_height = int(width * fabs(a) + height * fabs(b));
Point center = Point(srcImage.cols / 2, srcImage.rows / 2);
Mat map_matrix = getRotationMatrix2D(center, degree, 1.0);
map_matrix.at(0, 2) += (rotate_width - width) / 2; // 修改坐标偏移
map_matrix.at(1, 2) += (rotate_height - height) / 2; // 修改坐标偏移
warpAffine(srcImage, dstImage, map_matrix, { rotate_width, rotate_height }, CV_INTER_CUBIC);
imshow("旋转后的图像", dstImage);
waitKey();
return 0;
}
至此,图像的几何变换基本就完毕了,这里仍是推荐使用OpenCV官方提供的函数API来进行基本的几何变换,可是对于学习来讲,知道其原理仍是十分重要的,因此这里参考其余人的博客资料集合了一篇完整的解读。但愿可以对你有点帮助。
参考资料
数字图像处理与机器视觉Visual C与Matlab实现