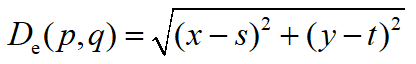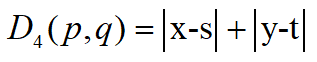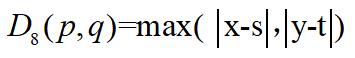图像处理（2-4章，图像获取、采样、量化、邻域、距离、点运算、代数运算、几何变换、镜像、傅里叶变换）
图像处理二、三、四章
- 第二章图像处理基础
-
- 2.2基础知识
-
- 2.2.1图像的数字化及表达
- 2.2.2图像的获取（扫描、采样、量化）
- 2.2.3像素间的基本关系（邻域、连通性、距离）
- 2.2.4图像的分类（位图，了解即可）
- 第三章图像基本运算
-
- 3.1图像基本运算的概述（了解即可）
- 3.2点运算
-
- 3.2.1线性点运算
-
- 3.1.2.2分段线性点运算（重点）
- 3.2.2非线性点运算（了解即可）
-
- 3.2.2.1对数变换（了解即可）
- 3.2.2.2幂次变换（了解即可）
- 点运算相关问答题
- 3.3代数运算与逻辑运算
-
- 3.3.1概念(了解即可)
- 3.3.1加法运算（重点）
- 3.3.2减法运算
- 3.3.3乘法运算
- 3.3.4除法运算
- 3.3.5逻辑运算（了解即可）
- 3.4几何运算（空间变化、重采样）
-
- 3.4.1图像的平移（了解即可）
- 3.4.2图像的镜像（重点）
- 3.4.3图像的旋转
- 3.4.4图像的缩放
- 3.4.5灰度重采样（最邻近法、双线插值法、三次插值法，了解即可）
- 第四章
-
- 4.2离散傅里叶变换matlab实现
ps：异或：相异为1；同或：相同为1
第二章图像处理基础
2.2基础知识
2.2.1图像的数字化及表达
（1）图像有单色与彩色、平面与立体、静止与动态、自发光与反射（透射）等区别
（2）任一幅图像，根据它的光强度(亮度、密度或灰度)的空间分布，均可以用下面的函数形式来表达.
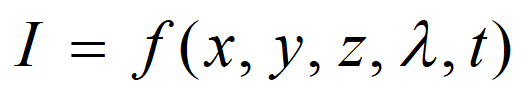
2.2.2图像的获取（扫描、采样、量化）
(1)图像获取
即图像的数字化过程，包括扫描、采样和量化。
(2)图像获取设备
由5个部分组成：采样孔，扫描机构，光传感器，量化器和输出存储体。
(3)关键技术
采样——成像技术；量化——模数转换技术。
采样：
①示意图
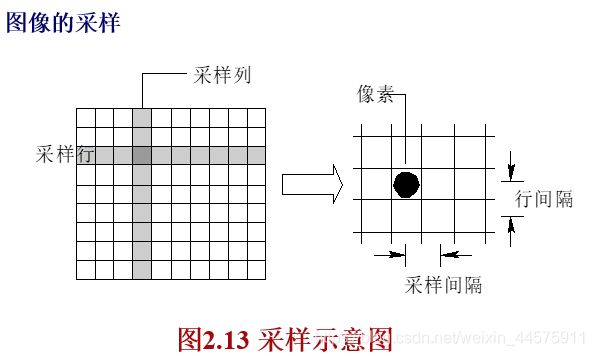
②效果
一般来说，采样间隔越大，所得图像像素数越少，空间分辨率低，质量差，严重时出现马赛克效应；
采样间隔越小，所得图像像素数越多，空间分辨率高，图像质量好，但数据量大。
量化：
①效果
量化等级越多，所得图像层次越丰富，灰度分辨率高，图像质量好，但数据量大；
量化等级越少，图像层次欠丰富，灰度分辨率低，会出现假轮廓现象，图像质量变差，但数据量小。
2.2.3像素间的基本关系（邻域、连通性、距离）
（1）邻域
设一个坐标为(x,y)，则：
①4邻域N4 ( p )为(x+1,y)，(x-1,y)，(x,y+1)，(x,y-1)；→←↑↓
②像素集ND（ p ）为(x+1,y+1)，(x+1,y-1)，(x-1,y+1)，(x-1,y-1)；↘↗↙↖
③8邻域N8 ( p )为N4 ( p ) ∪ ND（ p ）
ps：m邻接又叫混合邻接，是8邻接的改进，能消除8邻接产生的二义性
（2）连通性
为了确定两个像素是否连通，必须确定它们是否相邻及它们的灰度是否满足特定的相似性准则（或者说，它们的灰度值是否相等）
两个像素连通，即它们相邻且灰度相等
（3）距离（不用记公式，理解就行）
①欧氏距离
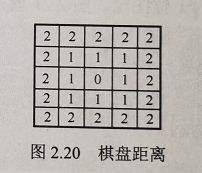
就是勾股定理…
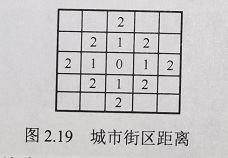
②D4距离（城市街区距离）
跟4邻域有关
ps：图片上的0是中心点，1、2是距离
③D8距离（棋盘距离）
跟8邻域有关
ps：图片上的0是中心点，1、2是距离
2.2.4图像的分类（位图，了解即可）
（1）分类
①动态特性
静止图像、运动图像
②色彩
灰度图像、彩色图像
③维数
二维图像、三维图像、多维图像
（2）位图
位图是通过许多像素点表示一幅图像，每个像素具有颜色属性和位置属性。
分为：
①二值图像
只有黑白两种颜色，一个像素点只占1bit，每个像素点只有两种取值，0（黑）和1（白）
②亮度图像
灰度图，8bit，28=256，介于黑白之间的256种灰度
③索引图像
颜色通过索引来的，图是彩色的（通过索引值所引导颜色表），最多只能显示256种颜色，也是8bit
④RGB图像
“真彩色”是RGB颜色的另一种叫法。
在RGB图像中，每一个像素由红、绿和蓝三个字节组成， 每个字节为8bit ，表示0到255之间的不同的亮度值，这三个字节组合可以产生1670万(256256256=16777216)种不同的颜色。
第三章图像基本运算
3.1图像基本运算的概述（了解即可）
按图像处理运算的数学特征, 图像基本运算可分为：
①点运算：点运算是指对一幅图像中每个像素点的灰度值进行计算的方法。
②代数运算：代数运算是指将两幅或多幅图像通过对应像素之间的加、减、乘、除运算得到输出图像的方法。
③逻辑运算：逻辑运算是指将两幅或多幅图像通过对应像素之间的逻辑与、或、非运算得到输出图像的方法。
④几何运算：几何运算就是改变图像中物体对象（像素）之间的空间关系。
从变换性质来分，几何变换可以分为图像的位置变换（平移、镜像、旋转）、形状变换（放大、缩小）以及图像的复合变换等。
3.2点运算
通过灰度变换函数完成点运算。设输入图像的灰度为f(x,y)，输出图像的灰度为g(x,y)，则点运算可以表示为：g(x,y)=T[f(x,y)]也可以写成s=T[r]，其中T[]为灰度变换函数，r为原灰度值，s为点运算后的灰度值。
点运算又称为“对比度增强”、“对比度拉伸”、“灰度变换”等，按灰度变换函数T[ ]的性质，可将点运算分为：
(5.2.2 基于直方图处理的图像增强)
3.2.1线性点运算
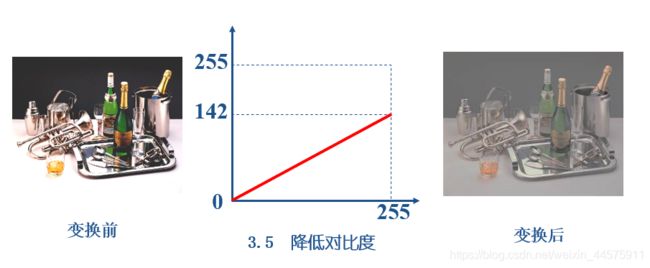
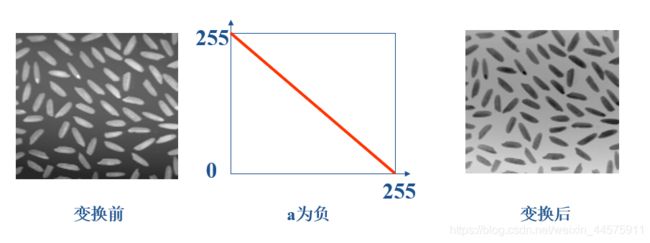
线性点运算的灰度变换函数形式可以采用线性方程描述，即s=ar+b
r是原灰度值，s是变换后灰度值
下图红线是s=r
(1)b=0时
①a>1为对比度增大，
②0
③a<0为图像求补，暗区变亮区，亮区变暗区。
（2）a=1时，b>0为图像变亮，b<0为图像变暗。
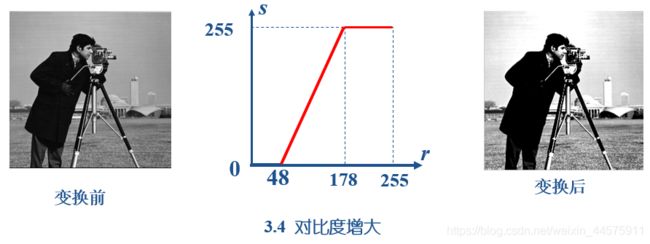
3.1.2.2分段线性点运算（重点）
（1）定义
将感兴趣的灰度范围线性扩展，相对抑制不感兴趣的灰度区域。
理解：只对特定范围内的灰度值进行线性运算。分段进行线性运算。
3.2.2非线性点运算（了解即可）
非线性点运算的输出灰度级与输入灰度级呈非线性关系，常见的非线性灰度变换为对数变换和幂次变换。
3.2.2.1对数变换（了解即可）
非线性拉伸不是对图像的整个灰度范围进行扩展，而是有选择地对某一灰度值范围进行扩展，其他范围的灰度值则有可能被压缩。
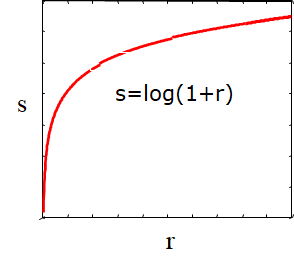
3.2.2.2幂次变换（了解即可）
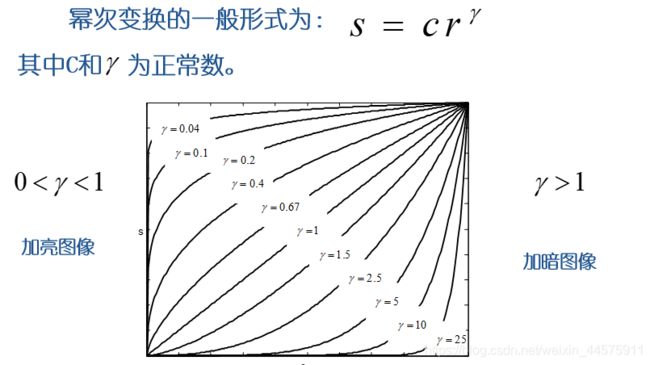
在γ=1下面的曲线是加暗，在γ=1上面的曲线是加亮，r是除以了255之后范围是0-1的灰度值
点运算相关问答题
（1）点运算是否会改变图像内像素点之间的空间位置关系？
答：不会。点运算是一种像素的逐点运算，它与相邻的像素之间没有运算关系，点运算不会改变图像内像素点之间的空间位置关系。
（2）对图像灰度的拉伸，非线性拉伸与分段线性拉伸的区别？
答：非线性拉伸 不是通过在不同灰度值区间选择不同的线性方程来实现对不同灰度值区间的扩展与压缩，而是在整个灰度值范围内采用统一的非线性变换函数，利用函数的数学性质实现对不同灰度值区间的扩展与压缩。
即：
①区别：
非线性拉伸-------->统一的非线性变换函数
分段线性拉伸----->不同灰度值区间选择不同的线性方程
②同：
二者都实现了对不同灰度值区间的扩展与压缩
3.3代数运算与逻辑运算
3.3.1概念(了解即可)
代数运算是指两幅或多幅输入图像之间进行点对点的加、减、乘、除运算得到输出图像的过程。如果记输入图像为A(x,y)和B(x,y)，输出图像为C(x,y)，则有如下四种形式：
逻辑运算是指将两幅或多幅图像通过对应像素之间的与、或、非逻辑运算得到输出图像的方法。在进行图像理解与分析领域比较有用。运用这种方法可以为图像提供模板，与其他运算方法结合起来可以获得某种特殊的效果。
3.3.1加法运算（重点）
（1）应用：
①去除”叠加性“随机噪音
②生成图像叠加效果
对原图像进行多次叠加不同的随机噪音得到不同的噪音图像集，再将噪音图像集取平均，即可得到降低噪音影响并且平滑了的图像。
利用同一图像的多幅加噪图像取平均、消除噪声。取M个图像相加求平均得到1幅新图像，一般选8幅取平均。
3.3.2减法运算
（1）定义
将同一景物在不同时间拍摄的图像或同一景物在不同波段的图像相减，这就是图像的减法运算。实际中常称为差影法。
（2）应用
差值图像提供了图像间的差值信息，能用于指导动态监测、运动目标的检测和跟踪、图像背景的消除及目标识别等。
主要应用举例：
①差影法(检测同一场景两幅图像之间的变化)
②混合图像的分离
3.3.3乘法运算
（1）定义
（2）应用
主要应用举例：
①图像的局部显示
②改变图像的灰度级
3.3.4除法运算
（1）定义
（2）应用
简单的除法运算可用于改变图像的灰度级，常用于遥感图像处理中。
3.3.5逻辑运算（了解即可）
ps：异或：相异为1；同或：相同为1
3.4几何运算（空间变化、重采样）
几何运算包括两个步骤，一个是空间变换，一个是重采样
3.4.1图像的平移（了解即可）
3.4.2图像的镜像（重点）
（1）定义
图像的镜像是指原始图像相对于某一参照面旋转180°的图像
3.4.3图像的旋转
一般图像的旋转是以图像的中心为原点，旋转一定的角度，即将图像上的所有像素都旋转一个相同的角度。
图像旋转之后，由于数字图像的坐标值必须是整数，因此，可能引起图像部分像素点的局部改变，因此，这时图像的大小也会发生一定的改变。
利用公式进行图像旋转正变换时需要注意如下两点：
1、为了避免图像信息的丢失，图像旋转后必须进行平移变换。
2、图像旋转之后，会出现许多空洞点，我们需要对这些空洞点必须进行填充处理，否则图像旋转后的效果不好，一般也称这种操作为插值处理，可采用行或列插值方法。最简单的插值方法是，图像旋转前某一点（x，y）的像素点颜色，除了填充在旋转后坐标（x’，y’）上外，还要填充（x’+1，y’）和（x’，y’+1）。即右、上
因为是cos、sin这些是小数，小数相乘然后取整会有位置误差，所以，图像旋转之后，可能会出现一些空白点，需要对这些空白点进行灰度级的插值处理，否则影响旋转后的图像质量。
3.4.4图像的缩放
以 a=1/2为例，即图像被缩小为原始图像的一半。图像被缩小一半以后根据目标图像和原始图像像素之间的关系，有如下两种缩小方法。
①取原图像的偶数行列组成新图像；
②取原图像的奇数行列组成新图像。
比如：
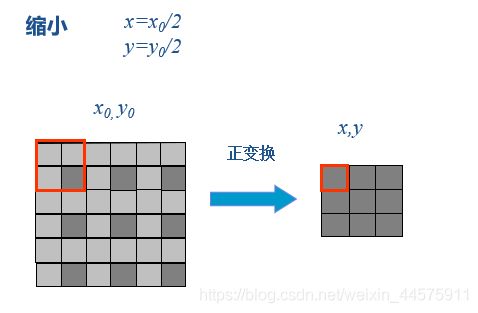
放大需要用到：邻近插值法和线性插值法
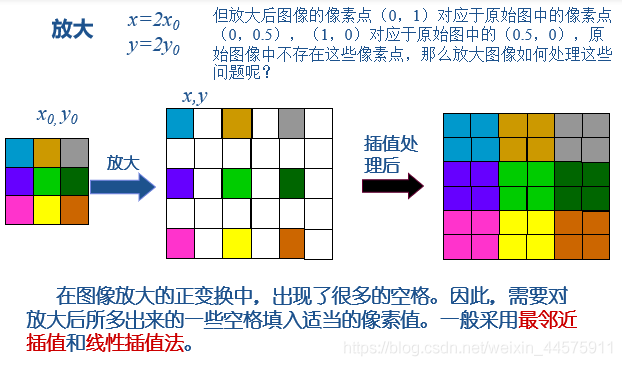
ps：所以缩小是一个降低像素值的过程，缩小之后再放大图像是会变糊的，因为缩小的时候图像信息缺失了。
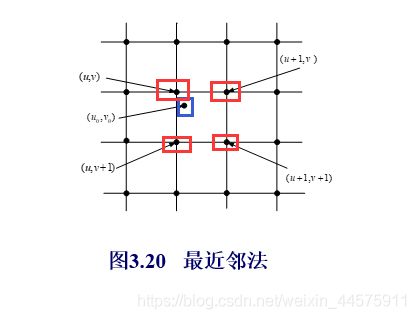
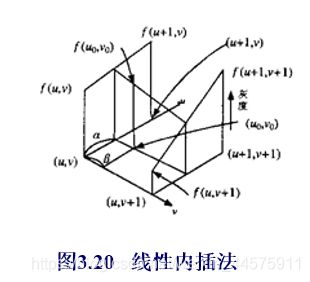
3.4.5灰度重采样（最邻近法、双线插值法、三次插值法，了解即可）
三种灰度插值方法—最近邻法、双线性插值法和三次内插法。
几何运算还需要一个算法用于灰度级的重采样。如果一个输出像素映射到四个输入像素之间，则其灰度值由灰度插值算法决定，如图蓝色的点的灰度值就取邻近的四个红色点的均值
第四章
4.2离散傅里叶变换matlab实现
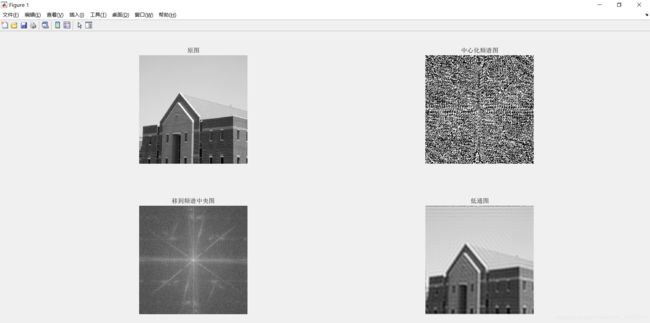
ps：（b）中，围绕坐标原点（中间亮的）是低频，向外是高频。
图像的能量主要集中在低频区，即图像的中央位置，而相对的高频区（左上、右上、左下、右下四个角）的幅值很小或接近于0。
因为傅里叶变换移频过后，低频部分到了中心位置，通常图像的低频占据了大部分信息，所以是白的亮的。
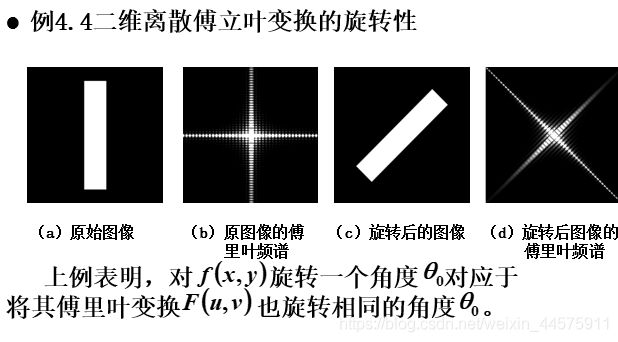
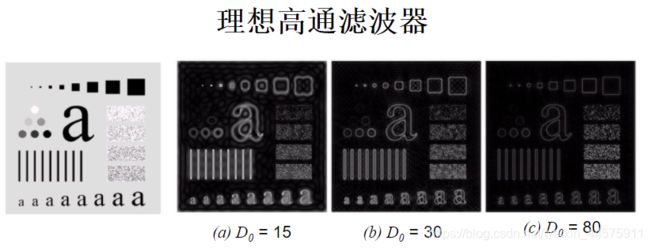
谱分布中，最亮区域表示其变换后的幅值最大。对图像傅里叶变换后中心移到零点后的结果，我们可以发现当长方形旋转了 45°时，频谱也跟着旋转45读，此实例验证了傅里叶变换的旋转性。
从上图实验结果可以看出，从幅值谱图像（b）中得到的信息比在相位谱图像（c）中得到的信息多，但对幅值谱图像重构（d）后，即忽略相位信息，将其设为0，所得到的图像与原始图像相比，结果差别很大；而对相位谱图像重构（e）后，及忽略幅值信息，将其设为常数，可以从中看出图像的基本轮廓来。
ps：高频是图像中的边缘、噪声，低通滤波能使图像平滑
ps：高通是只取了边缘
ps:matlab中是先高度再宽度的
