汉诺塔（图解演算+推导+Python实现）

汉诺塔

前言

关于汉诺塔的记忆很早就有了，无论还是益智玩具，还是电影片段

汉诺塔一直都是智力游戏的象征。

在后来的编程中，也接触到了汉诺塔。

时间线

时间	内容
2021年5月1日	完成初稿

故事背景

汉诺塔（Tower of Hanoi），又称河内塔，是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

问题延申：经典汉诺塔

在上面的故事背景中，如果有3根柱子，一根柱子上有n个盘子，盘子的大小从上往下逐渐增大。如何将一根柱子上的全部圆盘移动到另一个柱子上，进行场景模拟和统计移动次数。

逻辑演算

假设3根柱子分别是柱子a，b，c，柱子a上有n个盘子，设定为盘子1，盘子2等。大的盘子不可以在小的盘子的上面，即盘子2只能在盘子1的下面。

当n=1，n=2或者n=3很容易就能够演算出来，如下：

• n=1

直接将盘子1从柱子a迁移到柱子c即可，如图

• n=2

主要有3个步骤：

1. 将盘子1从柱子a移动到柱子b
2. 将盘子2从柱子a移动到柱子c
3. 将柱子b的盘子1移动到柱子c

如图

如果说n=1或者n=2的移动中没有发现些什么线索，那么下面的n=3将会是非常好的突破点

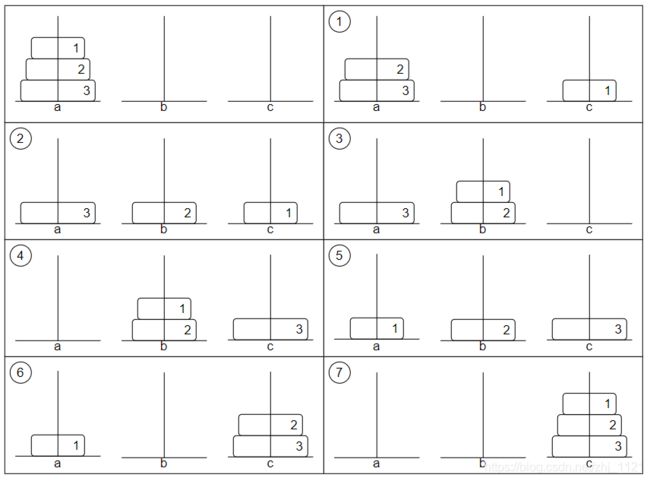
• n=3

按照游戏规则，则有以下步骤：

1. 将盘子1从柱子a移动到柱子c
2. 将盘子2从柱子a移动到柱子b
3. 将盘子1从柱子c移动到柱子b
4. 将盘子3从柱子a移动到柱子c
5. 将盘子1从柱子b移动到柱子a
6. 将盘子2从柱子b移动到柱子c
7. 将盘子1从柱子a移动到柱子c

如下：

正如前面所说，当n=1，n=2或者n=3时，移动的步骤很容易演算，但是如果n=4，或者n=100，那么步骤将会非常的多，所以需要对上面的演算结果进行分析，即对3种情况进行分析。

分析

• 当n=1时是非常简单的，将盘子1从柱子a移动到柱子c即可；

• 当n=2时，为了将最大的盘子2移动到柱子c，首先需要将盘子1移开后，才能进行。

当盘子1从柱子a移开后，此时有个非常关键的信息—柱子a就剩下一个盘子2了。

处理逻辑就变成了n=1的情况，即将盘子2从柱子a移动到柱子c；

此时，柱子a没有盘子，柱子b有一个盘子1，柱子c有一个盘子2

将盘子1从柱子b移动到柱子c即结束

抛开其它规则进行分析，移动的目的是将柱子a上除最大的盘子之外的盘子全部从柱子a上移开，**

**以保证将柱子a的最大的盘子移动到没有任何盘子的柱子c

有两个关键的信息：最大的盘子（即最底下的盘子），没有任何盘子的柱子c

根据这两个关键信息，则会有以下大体步骤：

1. 将除最大的盘子之外的盘子全部移动到柱子b
2. 最大的盘子移动到柱子c
3. 将柱子b的盘子全部移动到柱子c

注意一个细节：步骤1和步骤3的盘子规模是减1的

那么，根据这个原则，处理n=3的情况时，则有

• 当n=3时，将盘子1和盘子2移动到柱子b，将盘子3移动到柱子c

对n=3移动的步骤进行分析，有：

1. 将盘子1从柱子a移动到柱子c
2. 将盘子2从柱子a移动到柱子b
3. 将盘子1从柱子c移动到柱子b

对应步骤1：将除最大的盘子之外的盘子全部移动到柱子b

此时，问题规模减1，即如何将2个盘子从柱子a移动到柱子b

4. 将盘子3从柱子a移动到柱子c

对应步骤2：将最大的盘子移动到柱子c

1. 将盘子1从柱子b移动到柱子a
2. 将盘子2从柱子b移动到柱子c
3. 将盘子1从柱子a移动到柱子c

对应步骤3：将柱子b的盘子全部移动到柱子c

此时，问题规模减1，即如何将2和盘子从柱子b移动到柱子c

（关键）那么，当问题规模为n时，则会有

1. 将柱子a上的盘子1到盘子n-1移动到柱子b
2. 将柱子a的盘子n移动到柱子c
3. 将柱子b上的盘子1到盘子n-1全部移动到柱子c

总结

其实对上面的内容进行总结，可以发现处理的过程使用的是递归。理解的过程可以使用整体思想

拿n=3来说，盘子可以分为2类，将最大的盘子3和除最大的盘子之外的盘子（盘子1和盘子2）

可以将盘子1和盘子2看成是一个整体，那么问题就是如何将2个盘子从柱子a移动到柱子c了。所以也就有了3大步骤。

如下图：

图中，

背景绿色的对应步骤1（将除最大盘子之外的盘子移动到柱子b）

背景蓝色对应步骤2（将最大盘子移动到柱子c）

背景橙色对应步骤3（将柱子b上的盘子全部移动到柱子c）

所以，无论是多少个盘子，都可以按照n=2的模式解决。

代码处理

对象定义

最初的打算，是打印移动的信息就可以了，但是想了一下，还是使用数据结构模拟更真实的汉诺塔。

所以，使用面向对象的思想，定义柱子的数据结构和使用整形定义盘子的大小。

定义柱子

柱子主要有两个属性，分别是名称和容器。即柱子有自己的名称，也可以装盘子。

当然，还有一个特点，柱子类似于栈，即只能从栈顶弹出，装入栈顶。

定义盘子

相对于柱子的定义，盘子使用数值代表大小即可。所以直接使用整形即可。

动作定义

整个过程有一个动作，即将盘子从这个柱子移动到另一个柱子。可以拆解成两个动作—弹出和装入，

即将盘子从这个柱子弹出，再装入另一个柱子上

这里可以使用列表（从尾部放入，从尾部弹出）模拟栈

递归

可以发现，上面总结的3个步骤，其中步骤2是一次移动，而步骤1和步骤3是递归处理方式。

所以需要注意问题规模和递归出口

问题规模

由于每一次处理，问题规模都会-1，则递归函数的参数需要有一个问题规模，即n

递归出口

递归出口即只有一个盘子的时候，即n=1时，递归结束

计数

在问题延申中，有一个统计移动次数的要求。

这个要求的实现有两种方式—计算和推导，

计算，非常简单就能实现，即每移动一次，统计次数加1。

在代码实现中，只要定义全局变量即可。

其实从上面的逻辑演算，可以发现，最少移动次数是有规律的。

如

• n=1时，需要移动1次；

• n=2时，需要移动3次；

• n=3时，需要移动7次；

则很容易就能得到
$$count=2^n-1$$
分析（为什么会出现这一结果）

假设f(n)为移动n个盘子的次数，则f(n-1)为移动n-1个盘子的次数，

根据上面步骤，发现移动次数也是由3部分组成

• 当柱子a上有n个盘子时，需要将上面的n-1个盘子移动到柱子b，则移动次数为f(n-1)

• 将盘子n从柱子a移动到柱子c，则移动次数为1

• 将柱子b上的n-1个盘子移动到柱子c，则移动次数为f(n-1)

有
$$\begin{gathered} f(n)=f(n-1)+1+f(n-1)=2f(n-1)+1 \\ f(n)+1=2(f(n-1)+1) \\ g(n)=f(n)+1 \\ g(n)=2g(n-1) \end{gathered}$$
当n=1时，表示只有1个盘子，移动次数为1，
$$g(n)=f(n)+1=2$$
则有
$$\begin{gathered} g(n)=2^n \\ f(n)=g(n)-1=2^n-1 \end{gathered}$$
当n=1时，
$$f(n)=f(1)=1$$
所以有
$$count=f(n)=2^n-1$$

代码实现

class Pillar:
    def __init__(self,name):
        self.name = name
        self.res = []
    def pop(self):
        return self.res.pop(-1)
    def push(self,ele):
        self.res.append(ele)
    def print(self):
        print("柱子{}上的盘子:{}".format(self.name,self.res[::-1]))
class Hanoi:
    def __init__(self,n:int,a:str,b:str,c:str):
        self.count = 0
        self.a = Pillar(a)
        self.a.res = [n-i for i in range(n)]
        self.b,self.c = Pillar(b),Pillar(c)
    def print(self):
        print("当前柱子的情况（从上往下数）:")
        self.a.print()
        self.b.print()
        self.c.print()
    def move(self,f,t):
        ''' 将柱子f的最上面的盘子ele移动到柱子t '''
        if len(f.res) > 0 :
            t.res.append(f.res.pop(-1))
            self.count += 1
            print("第{}次移动：将柱子{}上的盘子{}移动到柱子{}".format(self.count,f.name,t.res[-1],t.name))
    def run(self,a,b,c,n):
        if n == 1:
            self.move(a, c)
        else:
            self.run(a, c, b, n-1)
            self.move(a, c)
            self.run(b, a, c, n-1)
if __name__ == "__main__":
    number = int(input("请输入一个数字："))
    a,b,c = "a","b","c"
    hanoi = Hanoi(number,a,b,c)
    hanoi.print()
    print("==========游戏开始==========")
    hanoi.run(hanoi.a,hanoi.b,hanoi.c,number)
    print("经历{}次移动".format(hanoi.count))
    print("==========游戏结束==========")
    hanoi.print()

运行结果

总结

其实，在编程中，汉诺塔往往与递归进行挂钩。

在经典汉诺塔中，从上面的推理和实现可以发现，并没有过多的描述递归。因为递归就像是俄罗斯套娃，一层套着一层，只有当最底下的娃娃打开以后，才知道最外层的娃娃有什么东西。因为在汉诺塔游戏中，通过脑力计算个位数的移动方式可以说都是一个挑战了，对于计算机并不是如此。但是如果盘子的数量达两位数，甚至更多，即使计算机也需要耗费时间。

所以，更多的是推导如何处理，在递归的处理方式下，使用整体的思想看待汉诺塔游戏。将盘子分为两类，即无论多少个盘子，都将盘子看成是两个整体—除最底下盘子之外的盘子和最底下的盘子。这么问题规模逐渐变小。

当然，由汉诺塔延申出来的问题也非常多，如多柱汉诺塔等等。也将会是非常有趣的问题。