lenet5卷积神经网络_PyTorch：卷积神经网络简介

本文主要研究了LeNet-5网络结构。

卷积神经网络是由一个或多个卷积层和顶端的全连接层（也可以使用1x1的卷积层作为最终的输出）组成一种前馈神经网络。一般的认为，卷积神经网络是由Yann LeCun在1989年提出的LeNet中首先被使用，但是由于当时的计算能力不够，并没有得到广泛的应用，到了1998年Yann LeCun及其合作者构建了更加完备的卷积神经网络LeNet-5并在手写数字的识别问题中取得成功，LeNet-5的成功使卷积神经网络的应用得到关注。LeNet-5沿用了LeCun (1989) 的学习策略并在原有设计中加入了池化层对输入特征进行筛选 。LeNet-5基本上定义了现代卷积神经网络的基本结构，其构筑中交替出现的卷积层-池化层被认为有效提取了输入图像的平移不变特征，使得对于特征的提取前进了一大步，所以我们一般的认为，Yann LeCun是卷积神经网络的创始人。

2006年后，随着深度学习理论的完善，尤其是计算能力的提升和参数微调（fine-tuning）等技术的出现，卷积神经网络开始快速发展，在结构上不断加深，各类学习和优化理论得到引入，2012年的AlexNet、2014年的VGGNet、GoogLeNet 和2015年的ResNet,使得卷积神经网络几乎成为了深度学习中图像处理方面的标配。

1. 卷积神经网络结构组成

1.1 卷积层

卷积计算

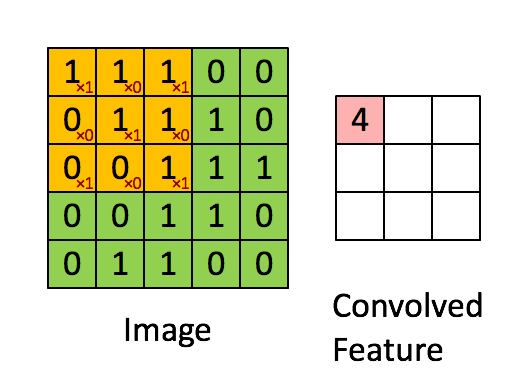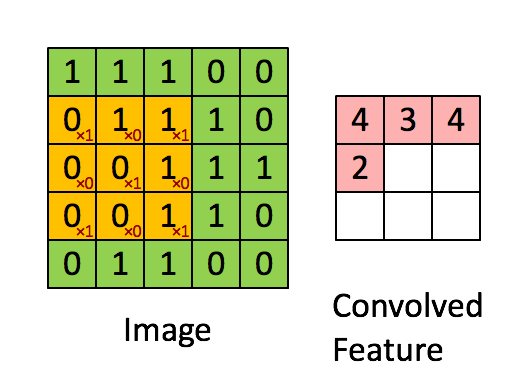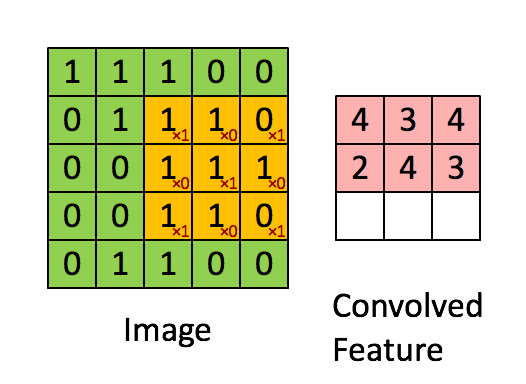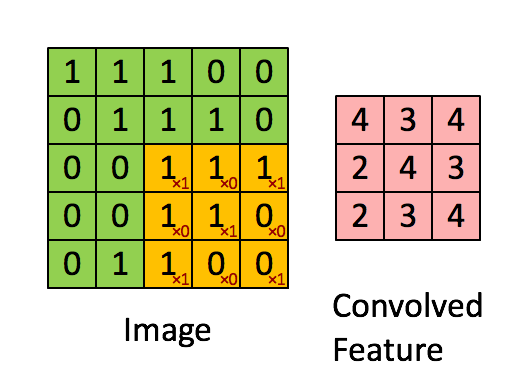
在介绍卷积层之前要先介绍一下卷积的计算，这里引用知乎上的一张图片：

我们会定义一个权重矩阵，也就是我们说的W（一般对于卷积来说，称作卷积的核kernel也有有人称做过滤器filter），这个权重矩阵的大小一般为3*3或者5*5，但是在LeNet里面还用到了比较大的7*7，现在已经很少见了，因为根据经验的验证，3和5是最佳的大小。 我们以图上所示的方式，我们在输入矩阵上使用我们的权重矩阵进行滑动，每滑动一步，将所覆盖的值与矩阵对应的值相乘，并将结果求和并作为输出矩阵的一项，依次类推直到全部计算完成。

上图所示，我们输入是一个5*5的矩阵，通过使用一次3*3的卷积核计算得到的计算结果是一个3*3的新矩阵。 那么新矩阵的大小是如何计算的呢？

卷积核大小 f：刚才已经说到了一个重要的参数，就是核的大小，我们这里用f来表示。

边界填充 (p)adding：我们看到上图，经过计算后矩阵的大小改变了，如果要使矩阵大小不改变呢，我们可以先对矩阵做一个填充，将矩阵的周围全部再包围一层，这个矩阵就变成了7*7,上下左右各加1，相当于5+1+1=7这时，计算的结果还是5*5的矩阵，保证了大小不变，这里的p=1。

步长 (s)tride：从动图上我们能够看到，每次滑动只是滑动了一个距离，如果每次滑动两个距离呢？那就需要使用步长这个参数。

计算公式：n为我们输入的矩阵的大小，

向下取整。

卷积层：在每一个卷积层中我们都会设置多个核，每个核代表着不同的特征，这些特征就是我们需要传递到下一层的输出，而我们训练的过程就是训练这些不同的核。

1.2 激活函数

由于卷积的操作也是线性的，所以也需要进行激活，一般情况下，都会使用relu。

1.3 池化层（pooling）

池化层是CNN的重要组成部分，通过减少卷积层之间的连接，降低运算复杂程度，池化层的操作很简单，就想相当于是合并，我们输入一个过滤器的大小，与卷积的操作一样，也是一步一步滑动，但是过滤器覆盖的区域进行合并，只保留一个值。 合并的方式也有很多种，例如我们常用的两种取最大值maxpooling，取平均值avgpooling。

池化层的输出大小公式也与卷积层一样，由于没有进行填充，所以p=0，可以简化为

。

1.4 dropout层

dropout是2014年 Hinton 提出防止过拟合而采用的方法，增强了模型的泛化能力 Dropout（随机失活）是指在深度学习网络的训练过程中，按照一定的概率将一部分神经网络单元暂时从网络中丢弃，相当于从原始的网络中找到一个更瘦的网络，说的通俗一点，就是随机将一部分网络的传播掐断，听起来好像不靠谱，但是通过实际测试效果非常好。 有兴趣的可以去看一下原文Dropout: A Simple Way to Prevent Neural Networks from Overfitting。

1.5 全连接层

全连接层一般是作为最后的输出层使用，卷积的作用是提取图像的特征，最后的全连接层就是要通过这些特征来进行计算，输出我们所要的结果了，无论是分类，还是回归。

我们的特征都是使用矩阵表示的，所以再传入全连接层之前还需要对特征进行压扁，将他这些特征变成一维的向量，如果要进行分类的话，就是用sofmax作为输出，如果要是回归的话就直接使用linear即可。

2. 经典模型

2.1 LeNet-5

1998， Yann LeCun 的 LeNet5 官网。

卷积神经网路的开山之作，麻雀虽小，但五脏俱全，卷积层、pooling层、全连接层，这些都是现代CNN网络的基本组件。

• 用卷积提取空间特征；
• 由空间平均得到子样本；
• 用 tanh 或 sigmoid 得到非线性；
• 用 multi-layer neural network作为最终分类器；
• 层层之间用稀疏的连接矩阵，以避免大的计算成本。

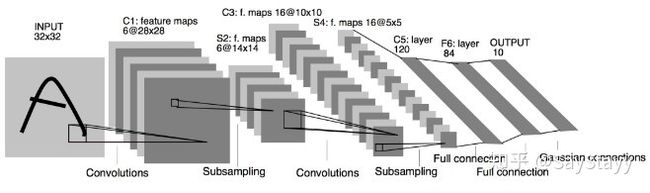
其网络结构如下：

1. C1层是一个卷积层，有6个卷积核（提取6种局部特征），核大小为5 * 5
2. S2层是pooling层，下采样（区域:2 * 2 ）降低网络训练参数及模型的过拟合程度。
3. C3层是第二个卷积层，使用16个卷积核，核大小:5 * 5 提取特征
4. S4层也是一个pooling层，区域:2*2
5. C5层是最后一个卷积层，卷积核大小:5 * 5 卷积核种类:120
6. 最后使用全连接层，将C5的120个特征进行分类，最后输出0-9的概率

输入：图像Size为32*32。这要比mnist数据库中最大的字母(28*28)还大。这样做的目的是希望潜在的明显特征，如笔画断续、角点能够出现在最高层特征监测子感受野的中心。

输出：10个类别，分别为0-9数字的概率。

以下代码来自PyTorch官方教程，为了便于理解，我打印了每步网络结构的尺寸。

import torch
import torch.nn as nn
import torch.nn.functional as F

class LeNet5(nn.Module):
    
    def __init__(self):
        super(LeNet5, self).__init__()
        # 1 input image channel, 6 output channels, 5x5 square convolution
        # kernel
        self.conv1 = nn.Conv2d(1, 6, 5)
        self.conv2 = nn.Conv2d(6, 16, 5)
        # an affine operation: y = Wx + b
        self.fc1 = nn.Linear(16 * 5 * 5, 120) # 这里论文上写的是conv,官方教程用了线性层
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84,  10)
    
    def forward(self, x):
        print(x.size()) 
        
        x = self.conv1(x)
        x = F.relu(x)
        print(x.size())
        
        # Max pooling over a (2, 2) window
        x = F.max_pool2d(x, (2, 2))
        print(x.size()) 
        
        x = self.conv2(x)
        x = F.relu(x)
        print(x.size()) 
        
        x = F.max_pool2d(x, (2,2))
        print(x.size()) 
        
        x = x.view(-1, self.num_flat_features(x))
        print(x.size()) 
        
        x = F.relu(self.fc1(x))
        print(x.size()) 
        
        x = F.relu(self.fc2(x))
        print(x.size()) 
        
        x = self.fc3(x)
        print(x.size()) 
        return x
    
    def num_flat_features(self, x):
        size = x.size()[1:] # all dimensions except the batch dimension,因为x是一个四维张量，[batch, channel, height, width]
        num_features = 1
        for s in size:
            num_features *= s
        return num_features
    
net = LeNet5()
print(net)

LeNet5(
(conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
(conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
(fc1): Linear(in_features=400, out_features=120, bias=True)
(fc2): Linear(in_features=120, out_features=84, bias=True)
(fc3): Linear(in_features=84, out_features=10, bias=True)
)

# net.named_parameters可同时返回可学习的参数及名称
for name, parameters in net.named_parameters():
    print(name, ':', parameters.size())

conv1.weight : torch.Size([6, 1, 5, 5])
conv1.bias : torch.Size([6])
conv2.weight : torch.Size([16, 6, 5, 5])
conv2.bias : torch.Size([16])
fc1.weight : torch.Size([120, 400])
fc1.bias : torch.Size([120])
fc2.weight : torch.Size([84, 120])
fc2.bias : torch.Size([84])
fc3.weight : torch.Size([10, 84])
fc3.bias : torch.Size([10])

然后打印每层网络输出的大小：

input = torch.randn(1, 1, 32, 32) # 这里的对应前面forward的输入是32
out = net(input)

torch.Size([1, 1, 32, 32])
torch.Size([1, 6, 28, 28])
torch.Size([1, 6, 14, 14])
torch.Size([1, 16, 10, 10])
torch.Size([1, 16, 5, 5])
torch.Size([1, 400])
torch.Size([1, 120])
torch.Size([1, 84])
torch.Size([1, 10])

2.2 AlexNet

2012，Alex Krizhevsky 可以算作LeNet的一个更深和更广的版本，可以用来学习更复杂的对象论文。

• 用rectified linear units（ReLU）得到非线性；
• 使用 dropout 技巧在训练期间有选择性地忽略单个神经元，来减缓模型的过拟合；
• 重叠最大池，避免平均池的平均效果；
• 使用 GPU NVIDIA GTX 580 可以减少训练时间，这比用CPU处理快了 10 倍，所以可以被用于更大的数据集和图像上

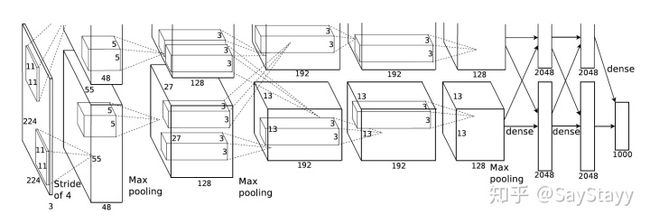
虽然 AlexNet只有8层，但是它有60M以上的参数总量，Alexnet有一个特殊的计算层，LRN层，做的事是对当前层的输出结果做平滑处理，这里就不做详细介绍了， Alexnet的每一阶段（含一次卷积主要计算的算作一层）可以分为8层：

1. conv - relu - pooling - LRN ： 要注意的是input层是227*227，而不是paper里面的224，这里可以算一下，主要是227可以整除后面的conv1计算，224不整除。如果一定要用224可以通过自动补边实现，不过在input就补边感觉没有意义，补得也是0，这就是我们上面说的公式的重要性。
2. conv - relu - pool - LRN ： group=2，这个属性强行把前面结果的feature map分开，卷积部分分成两部分做
3. conv - relu
4. conv-relu
5. conv - relu - pool
6. fc - relu - dropout ： dropout层，在alexnet中是说在训练的以1/2概率使得隐藏层的某些neuron的输出为0，这样就丢到了一半节点的输出，BP的时候也不更新这些节点，防止过拟合。
7. fc - relu - dropout
8. fc - softmax

在Pytorch的vision包中是包含Alexnet的官方实现的，我们直接使用官方版本看下网络：

import torchvision
model = torchvision.models.alexnet(pretrained=False) #我们不下载预训练权重
print(model)

AlexNet(
(features): Sequential(
(0): Conv2d(3, 64, kernel_size=(11, 11), stride=(4, 4), padding=(2, 2))
(1): ReLU(inplace=True)
(2): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
(3): Conv2d(64, 192, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
(4): ReLU(inplace=True)
(5): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
(6): Conv2d(192, 384, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(7): ReLU(inplace=True)
(8): Conv2d(384, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(9): ReLU(inplace=True)
(10): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(11): ReLU(inplace=True)
(12): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
)
(avgpool): AdaptiveAvgPool2d(output_size=(6, 6))
(classifier): Sequential(
(0): Dropout(p=0.5, inplace=False)
(1): Linear(in_features=9216, out_features=4096, bias=True)
(2): ReLU(inplace=True)
(3): Dropout(p=0.5, inplace=False)
(4): Linear(in_features=4096, out_features=4096, bias=True)
(5): ReLU(inplace=True)
(6): Linear(in_features=4096, out_features=1000, bias=True)
)
)

此外，还有其他流行的网络结构，比如VGG、GooLeNet、ResNet，学到再仔细介绍。