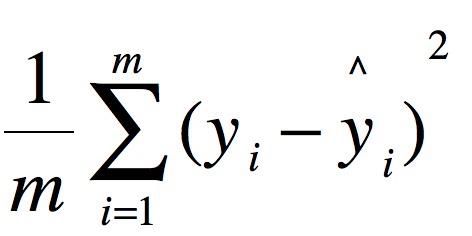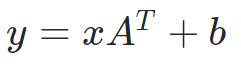深度之眼pytorch打卡(四)| 台大李宏毅机器学习 2020作业(一):线性回归,实现多因素作用下的PM2.5预测(Pytorch版手写+nn.Linear())
前言
这里主要是用Pytorch重新写一下李宏毅机器学习的作业一,那里主要是用pandas和numpy来实现的数据操作,这里将用Pytorch工具来写线性回归,实现多因素作用下的PM2.5预测。本笔记主要是为了熟悉一下Pytorch张量与张量的创建与Pytorch张量操作,两篇笔记中涉及的张量创建函数与张量操作函数的使用。
原理分析见:台大李宏毅 机器学习 2020学习笔记(二):回归与过拟合
数据分析见:台大李宏毅机器学习 2020作业(一):手写线性回归,实现多因素作用下的PM2.5预测
代码及资料:lhy_PM2.5_pytorch.zip或者本笔记末尾网盘链接
任务
- 处理数据
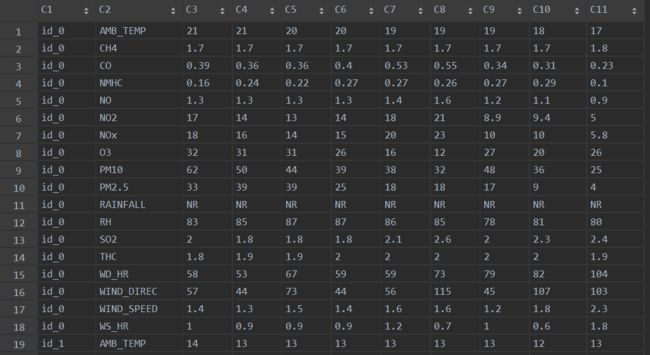
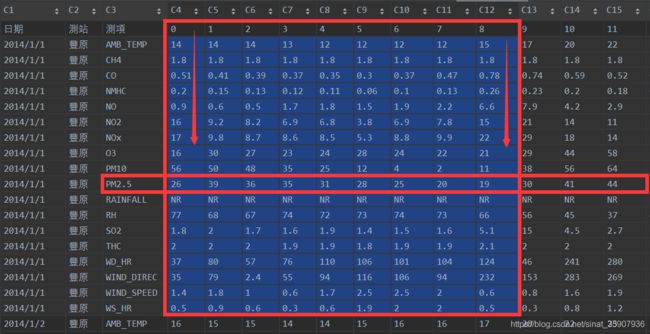
从我的另一篇笔记中,我们可以知道训练数据是一个(18x20x12)*24的二维表格。24指一天24小时,18指18个特征,如温度值、降雨值、PM2.5等,20指一个月有20天的数据,然后12指一年12个月。训练数据部分截图如图1所示,可以发现数据的存放方式是很奇怪的,没有办法直接作为训练集使用,所以我们需要改变它。我们希望每一组输入数据都展成一行,以便于与w做点乘,这就是转换的目标。
需要预测的数据是一个(18x240)* 9的二维表格,如图2。240个id,每个id给了前9个小时的数据,每个数据18个特征。要求我们通过每个id前9个小时的数据,来预测其第10个小时PM2.5值。我们当然可以只用前9个小时的PM2.5值作为特征,然后预测第10个小时的PM2.5的值,但是这样不准确。所以,最后用数据前9个小时的所有数据作为特征,共(18 *9)个特征,来预测第10个小时的PM2.5值。
- 训练模型
模型:多元线性函数
损失:MSE loss
优化:梯度下降
- 预测
输出测试数据中每个id第10个小时的PM2.5值。
处理数据
- 载入数据并转换成张量
同样的,用pandas来读入big5编码的csv文件。然后将读入的数据先转换成numpy,然后用from_numpy函数将数据再转换成tensor。
import pandas as pd
import matplotlib.pyplot as plt
import torch
data = pd.read_csv('./data/train.csv', encoding='big5')
data = data.iloc[:, 3:] # 去掉前三列,即非数据列
data[data == 'NR'] = 0 # 将rainfall里的NR换成0,即不下雨为0
raw_data = data.to_numpy().astype(float) # 将pandas转换成numpy,再转换成tensor
data_tensor = torch.from_numpy(raw_data)
print(data_tensor.shape, '\n', data_tensor[0:2])
输出前两行结果,与原数据比对,相同,说明没有问题。
2014/1/1 AMB_TEMP 14 14 14 13 12 12 12 12 15 17 20 22 22 22 22 22 21 19 17 16 15 15 15 15
2014/1/1 CH4 1.8 1.8 1.8 1.8 1.8 1.8 1.8 1.8 1.8 1.8 1.8 1.8 1.8 1.8 1.8 1.8 1.8 1.8 1.8 1.8 1.8 1.8 1.8 1.8
torch.Size([4320, 24])
tensor([[14.0000, 14.0000, 14.0000, 13.0000, 12.0000, 12.0000, 12.0000, 12.0000,
15.0000, 17.0000, 20.0000, 22.0000, 22.0000, 22.0000, 22.0000, 22.0000,
21.0000, 19.0000, 17.0000, 16.0000, 15.0000, 15.0000, 15.0000, 15.0000],
[ 1.8000, 1.8000, 1.8000, 1.8000, 1.8000, 1.8000, 1.8000, 1.8000,
1.8000, 1.8000, 1.8000, 1.8000, 1.8000, 1.8000, 1.8000, 1.8000,
1.8000, 1.8000, 1.8000, 1.8000, 1.8000, 1.8000, 1.8000, 1.8000]],
dtype=torch.float64)
- 数据形状变换
将原先训练数据每天的24小时,18个特征,纵向排列的方式,转变成横向排列的方式,即将每天的数据依次横向首尾相接,最后构成一个形状(24* 12* 240)*18的二维张量。张量操作上是先切,再合,要用到split和cat两个方法,用法见此

tensor_split = torch.split(data_tensor, 18, dim=0) # 由于是18个特征,所以切分尺寸是18
print(tensor_split[0].shape, len(tensor_split))
# tensor_cat = torch.cat([tensor_split[0], tensor_split[1]], dim=1)
tensor_cat = tensor_split[0]
for i in range(len(tensor_split)-1):
tensor_cat = torch.cat([tensor_cat, tensor_split[i+1]], dim=1)
print(tensor_cat.shape, len(tensor_cat[0]))
print(tensor_cat[0][0:48])
输出第一行前48个数据,与原数据比对,相同,说明没有问题。
2014/1/1 AMB_TEMP 14 14 14 13 12 12 12 12 15 17 20 22 22 22 22 22 21 19 17 16 15 15 15 15
2014/1/2 AMB_TEMP 16 15 15 14 14 15 16 16 17 20 22 23 24 24 24 24 23 21 20 19 18 18 18 18
torch.Size([18, 5760]) 5760
tensor([14., 14., 14., 13., 12., 12., 12., 12., 15., 17., 20., 22., 22., 22.,
22., 22., 21., 19., 17., 16., 15., 15., 15., 15., 16., 15., 15., 14.,
14., 15., 16., 16., 17., 20., 22., 23., 24., 24., 24., 24., 23., 21.,
20., 19., 18., 18., 18., 18.], dtype=torch.float64)
由于预测的时候,要通过前九个小时的数据来预测第十个小时的PM2.5值。所以,训练集的每一组数据都应该由两个部分组成:前九个小时的数据,共9* 18=162个,reshape到一维行向量,是数据本身,第10个小时的PM2.5值就是目标或者标签。采用移位取值的方式来获得数据,步长为1,每次取10个数据,那么可以产生(5760-10)/1 +1=5751组数据。
tensor_t = torch.t(tensor_cat) # 转置一下,后面reshape后才是一天的18个特征,接另一天的18个特征...这样组成一个行张量。
tensor_x = torch.empty(len(tensor_t)-10+1, 18*9)
tensor_y = torch.empty(len(tensor_t)-10+1, 1)
print(tensor_t.shape, len(tensor_t), tensor_x.shape, tensor_y.shape)
for j in range(len(tensor_t)-10+1):
tensor_x[j] = torch.reshape(tensor_t[j:j+9], [1, -1]) #9行展成一行
tensor_y[j] = tensor_t[j+9][9]
print(tensor_x[0], '\n', tensor_y[0:10])
观察数据集第一组数据与图4所示的原始数据,可见他们是相同的,说明没有错误。另外输出的前十个对比标签与原数据中PM2.5值,也是相符的。
30 41 44 33 37 36 45 42 49 45
torch.Size([5760, 18]) 5760 torch.Size([5751, 162]) torch.Size([5751, 1])
tensor([1.4000e+01, 1.8000e+00, 5.1000e-01, 2.0000e-01, 9.0000e-01, 1.6000e+01,
1.7000e+01, 1.6000e+01, 5.6000e+01, 2.6000e+01, 0.0000e+00, 7.7000e+01,
1.8000e+00, 2.0000e+00, 3.7000e+01, 3.5000e+01, 1.4000e+00, 5.0000e-01,
1.4000e+01, 1.8000e+00, 4.1000e-01, 1.5000e-01, 6.0000e-01, 9.2000e+00,
9.8000e+00, 3.0000e+01, 5.0000e+01, 3.9000e+01, 0.0000e+00, 6.8000e+01,
2.0000e+00, 2.0000e+00, 8.0000e+01, 7.9000e+01, 1.8000e+00, 9.0000e-01,
1.4000e+01, 1.8000e+00, 3.9000e-01, 1.3000e-01, 5.0000e-01, 8.2000e+00,
8.7000e+00, 2.7000e+01, 4.8000e+01, 3.6000e+01, 0.0000e+00, 6.7000e+01,
1.7000e+00, 2.0000e+00, 5.7000e+01, 2.4000e+00, 1.0000e+00, 6.0000e-01,
1.3000e+01, 1.8000e+00, 3.7000e-01, 1.2000e-01, 1.7000e+00, 6.9000e+00,
8.6000e+00, 2.3000e+01, 3.5000e+01, 3.5000e+01, 0.0000e+00, 7.4000e+01,
1.6000e+00, 1.9000e+00, 7.6000e+01, 5.5000e+01, 6.0000e-01, 3.0000e-01,
1.2000e+01, 1.8000e+00, 3.5000e-01, 1.1000e-01, 1.8000e+00, 6.8000e+00,
8.5000e+00, 2.4000e+01, 2.5000e+01, 3.1000e+01, 0.0000e+00, 7.2000e+01,
1.9000e+00, 1.9000e+00, 1.1000e+02, 9.4000e+01, 1.7000e+00, 6.0000e-01,
1.2000e+01, 1.8000e+00, 3.0000e-01, 6.0000e-02, 1.5000e+00, 3.8000e+00,
5.3000e+00, 2.8000e+01, 1.2000e+01, 2.8000e+01, 0.0000e+00, 7.3000e+01,
1.4000e+00, 1.8000e+00, 1.0600e+02, 1.1600e+02, 2.5000e+00, 1.9000e+00,
1.2000e+01, 1.8000e+00, 3.7000e-01, 1.0000e-01, 1.9000e+00, 6.9000e+00,
8.8000e+00, 2.4000e+01, 4.0000e+00, 2.5000e+01, 0.0000e+00, 7.4000e+01,
1.5000e+00, 1.9000e+00, 1.0100e+02, 1.0600e+02, 2.5000e+00, 2.0000e+00,
1.2000e+01, 1.8000e+00, 4.7000e-01, 1.3000e-01, 2.2000e+00, 7.8000e+00,
9.9000e+00, 2.2000e+01, 2.0000e+00, 2.0000e+01, 0.0000e+00, 7.3000e+01,
1.6000e+00, 1.9000e+00, 1.0400e+02, 9.4000e+01, 2.0000e+00, 2.0000e+00,
1.5000e+01, 1.8000e+00, 7.8000e-01, 2.6000e-01, 6.6000e+00, 1.5000e+01,
2.2000e+01, 2.1000e+01, 1.1000e+01, 1.9000e+01, 0.0000e+00, 6.6000e+01,
5.1000e+00, 2.1000e+00, 1.2400e+02, 2.3200e+02, 6.0000e-01, 5.0000e-01])
tensor([[30.],
[41.],
[44.],
[33.],
[37.],
[36.],
[45.],
[42.],
[49.],
[45.]])
- 数据标准化
用公式标准化: 要求均值和方差
torch.mean(input, dim, keepdim=False, out=None) → Tensor
dim: 在给定维度的每一行做平均。
keepdim: keepdim=False表示输出的张量会被squeeze,即长度为1的维度会被压缩。
torch.std(input, dim, keepdim=False, unbiased=True, out=None)
unbiased: unbiased=Falsee表示有偏估计
用函数标准化: 用Pytorch给的标准化函数,此处用1维
torch.nn.BatchNorm1d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
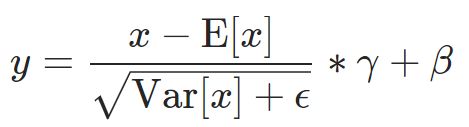
affine: 当为false是不考虑两个参数,r和B,这是两个可以学习的参数,目的是通过数据来决定是否需要标准化,或者是标准化的程度。
eps: 避免分母为零的一个极小值,一般取1e-05
# 用标准化公式
mean_x = torch.mean(tensor_x, dim=0, keepdim=True)
std_x = torch.std(tensor_x, dim=0, keepdim=True)
print(mean_x.shape, std_x.shape)
tensor_norm = torch.div(torch.sub(tensor_x, mean_x), std_x)
# pytorch 一维的标注化函数
tensor_norml = torch.nn.BatchNorm1d(162, affine=False, momentum=0.)
tensor_nn_norm = tensor_norml(tensor_x)
print(tensor_norm, '\n', tensor_nn_norm)
如图5,两种方法结果的对比,基本上没有什么差别说明公式是写正确了的,另外可能这个细微的差别是由eps引起的。
- 数据集拆分
用数据集前80%做训练集,后20%做验证集,用于判断是否过拟合,当然线性模型是不可能过拟合的,这里就当成测试集来用。
floor: 向下取整
x = torch.cat([torch.ones(len(tensor_nn_norm_x), 1), tensor_nn_norm_x], dim=1) # 为1那一列是bias前的系数
w = torch.randn([18*9+1, 1], requires_grad=True) # 需要求梯度
train_x = x[:math.floor(0.8*len(x))]
train_y = tensor_y[:math.floor(0.8*len(x))]
val_x = x[math.floor(0.8*len(x)):]
val_y = tensor_y[math.floor(0.8*len(x)):]
print(train_x.shape, train_y.shape, val_x.shape, val_y.shape)
结果:输出两个张量形状。
torch.Size([4600, 163]) torch.Size([4600, 1]) torch.Size([1151, 163]) torch.Size([1151, 1])
训练模型
- 手写实现
矩阵点乘函数:
torch.mm(input, mat2, out=None) # 矩阵点乘,注意维度
迭代部分代码:由于w需要求梯度,所以在创建该张量时需要requires_grad=True。另外张量的梯度需要手动清零,grad.zero_(),如果不清零会一直累加,最后可能导致梯度爆炸。
MSE:均方根误差函数
lr = 0.06 # 大于0.06,会发散
it_time = 1000
y_train_loss = torch.empty(it_time, 1)
y_val_loss = torch.empty(int(it_time/100), 1)
print(y_val_loss.shape)
for iteration in range(it_time):
wx = torch.mm(train_x, w) # 前向传播
loss = (0.5 * (train_y - wx) ** 2).mean() # 计算 MSE loss
loss.backward() # 反向传播
y_train_loss[iteration] = loss
w.data.sub_(lr*w.grad) # w = w - lr*w.grad
w.grad.zero_() # w的梯度清零,如果不清零,会一直累加
if iteration%100 == 0 and iteration!=0:
wx_val = torch.mm(val_x, w)
y_val_loss[int(iteration/100)] = (0.5 * (val_y - wx_val) ** 2).mean()
print(y_train_loss.shape, y_val_loss.shape)
val_j = range(0, it_time, 100)
plt.figure()
plt.grid()
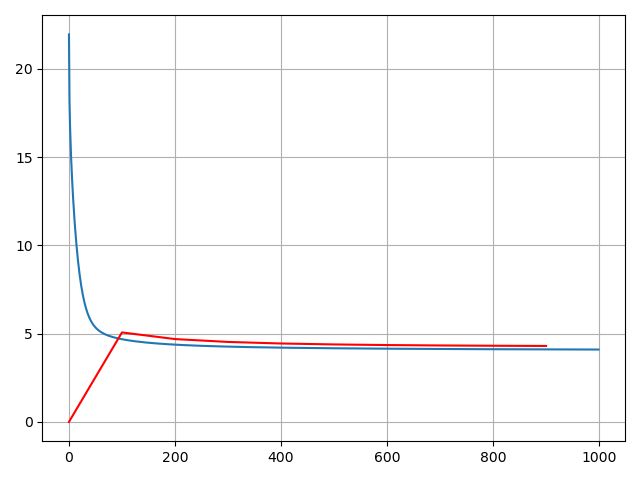
plt.plot(torch.sqrt(y_train_loss).data.numpy())
plt.plot(val_j, torch.sqrt(y_val_loss).data.numpy(), 'r-')
plt.show()
torch.Size([10, 1])
torch.Size([1000, 1]) torch.Size([10, 1])
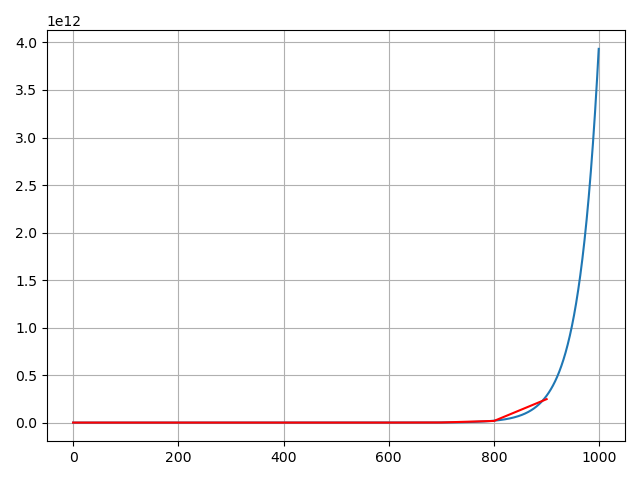
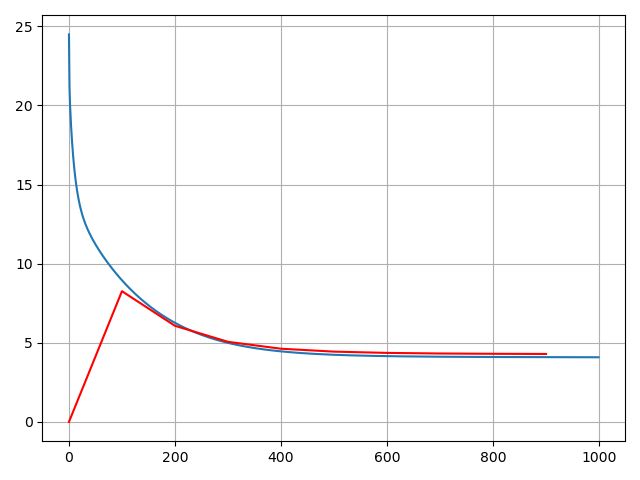
损失曲线: 蓝色为训练集上损失,红色为验证集上损失
lr=0.063,爆炸,即会出现一堆[nan],[nan],[nan]…,就是数据超出最大表示范围了。
- nn.Linear()
torch.nn.Linear(in_features, out_features, bias=True)
torch.nn.MSELoss(size_average=None, reduce=None, reduction='mean')
基本流程:模型实例化->损失函数实例化->优化器实例化;
前向传播->计算loss->反向传播->更新参数->梯度清零;
torch.optim.SGD(params, lr=<required parameter>, momentum=0, dampening=0, weight_decay=0, nesterov=False)
lr = 0.02
it_time = 1000
# 模型、损失函数和优化器实例化
model = torch.nn.Linear(163, 1, bias=False) # nn.Linear实例化由于前面添加bias进w了,所以这里就不要bias了
loss_function = torch.nn.MSELoss() # 使用均方根误差函数
optimizer = torch.optim.SGD(model.parameters(), lr=lr) # 优化器选择随机梯度下降
# 迭代
for iteration in range(it_time):
# 数据和标签
inputs = train_x
targets = train_y
# 前向传播
outputs = model(inputs)
loss = loss_function(outputs, targets)
# 反向传播
optimizer.zero_grad() # 梯度清零
loss.backward()
optimizer.step() # 只有用了这个函数模型才会更新
y_train_loss[iteration] = loss.item()
if iteration%100 == 0 and iteration != 0:
val_outputs = model(val_x)
y_val_loss[int(iteration / 100)] = loss_function(val_outputs, val_y).item()
torch.save(model.state_dict(), 'model/net.pth')
这个的学习率需要更小,0.05直接爆炸,应该是函数MSE前面没有乘0.5导致的。
预测
- 代码
import pandas as pd
import csv
import torch
test_data = pd.read_csv('./data/test.csv', encoding='big5', header=None)
test_data = test_data.iloc[:, 2:]
test_data[test_data == 'NR'] = 0
test_raw_data = test_data.to_numpy().astype(float)
test_tensor = torch.from_numpy(test_raw_data)
test_x = torch.zeros(240, 18*9)
test_split = torch.split(test_tensor, 18, dim=0)
print(len(test_split))
for i in range(len(test_split)):
test_x[i] = torch.reshape(torch.t(test_split[i]), [1, -1]) # 注意此处要转置,因为处理训练集的时候转置了,而且转置之后才是比较和逻辑的。
print(test_x[0])
norm = torch.nn.BatchNorm1d(162, affine=False, momentum=0.) # 标准化
test_x = norm(test_x)
x = torch.cat([torch.ones(len(test_x), 1), test_x], dim=1)
# print(x)
print(x.shape)
w = torch.load('weights.pt')
y_pred = torch.mm(x, w)
# 用nn模型预测
# model = torch.nn.Linear(163, 1, bias=False) # nn.Linear实例化由于前面添加bias进w了,所以这里就不要bias了
# model.load_state_dict(torch.load('model/net.pth'))
# y_pred = model(x)
# print(y_pred)
y_pred_sq = torch.squeeze(y_pred) # 压缩维度
with open('predict.csv', mode='w', newline='') as file:
csv_writer = csv.writer(file)
header = ['id', 'PM2.5']
csv_writer.writerow(header)
for j in range(len(y_pred_sq)):
if int(y_pred_sq[j]) < 0:
row = ['id_'+str(j), '0']
else:
row = ['id_' + str(j), str(int(y_pred_sq[j]))]
csv_writer.writerow(row)
- 结果
有将此下结果与台大李宏毅机器学习 2020作业(一):手写线性回归,实现多因素作用下的PM2.5预测这篇笔记对比,基本上是一样的。如果要细致的对比,可以计算一下两者的距离,我相信,肯定是比较小的。
参考
https://blog.csdn.net/veritasalice/article/details/103890510
https://blog.csdn.net/weixin_42147780/article/details/102544614?depth_1-utm_source=distribute.pc_relevant.none-task-blog-OPENSEARCH-17&utm_source=distribute.pc_relevant.none-task-blog-OPENSEARCH-17
https://pan.baidu.com/s/1hq-YtOJMsYRsRmIDLJtRrw 提取码:jkuq