单子
单子(Monad)是一种将函子组合应用的方法。在计算机科学里,单子经常用来代表计算(computation)。单子能用来把与业务无关的通用程序行为抽象出来,比如有用来处理并行(Future)、异常(Option和Try等)、甚至副作用的单子。
单子的flatMap和unit操作作为构建数据类型的基本操作,可以实现很多复杂的高阶函数。
单子的程序描述
Monad定义了unit和flatMap两个函数。Monad都是Functor,因为我们可以用flatMap+unit来实现map。我们可以定义Monad继承自Functor特质。
trait Functor[F[_]] {
def map[A, B](fa: F[A])(f: A => B): F[B]
}
trait Monad[M[_]] extends Functor[M] {
def unit[A](a: A): M[A]
def flatMap[A, B](ma: M[A])(f: A => M[B]): M[B]
}
- unit可以看成是Monad的构造函数或者工厂函数,它用来创建一个Monad实例。unit表示“装箱”。
- flatMap和map函数类似,不同的是它接受的参数f返回的是M[B]。flatMap会对Monad里的每一个元素都产生一个新的Monad容器,然后所有这些容器里的元素会被取出,而组合到一个Monad容器里。
- unit,map,flatMap是Monad的三个必要函数,其中map可以由unit和flatMap来实现
def map[A, B](f: A => B): M[B] =
flatMap(a => unit(f(a)))
Monad类代码
上面是定义了Monad特质,定义了Monad需要实现的unit和flatMap接口,而实际的monad是指M[_]这个类型构造器。
而下面的M则是指一个Monad类:
class M[A] {
def flatMap[B](f: A => M[B]): M[B] = ...
}
def unit[A](x: A): M[A] = ...
其他风格的Monad代码
有的Monad风格是这样的:
trait Monad[M[_]] {
def unit[A](a: A): M[A]
def flatten[A](mma: M[M[A]]): M[A]
}
上面的flatten也叫join或者bind,它接受一个包裹两层的类型,转换成包裹一层的类型。
其实flatten可以通过flatMap推导出来,def flatten[A](mma: M[M[A]]): M[A] = flatMap(mma)(ma => ma),所以这个定义和之前的Monad特质的定义时等价的。
单子法则
结合性法则(associative law)
flatMap满足结合性法则
m flatMap f flatMap g == m flatMap (x => f(x) flatMap g)
Kleisli组合法则(kleisli composition)
Monoid的结合性操作op(a, op(b, c)) == op(op(a, b), c),这对于Monad来说,用flatMap难以表达该操作。
如果不对Monadic值M[A]进行结合性操作,而是对Monadic函数A => M[B]证明结合性操作就会相对容易。
A => M[B]是瑞士数学家Heinrich Kleisli法则的箭头(Kleisli Arrow)。我们可以用Kleisli Arrow来实现一个函数compose:
def compose[A, B, C](f: A => M[B], g: B => M[C]): A => M[C] =
a => flatMap(f(a))(g)
compose函数满足compose(f,compose(g,h)) == compose(compose(f,g),h)。
恒等法则(identity law)
在Monoid中,identity相对于op操作的作用,在Monad中,unit操作是compose函数的元函数。
通过unit我们可以证明Monad的左右恒等:
compose(f,unit) == f
compose(unit,f) == f
unit操作还满足下面两个等式:
unit(x) flatMap f == f(x)
m flatMap unit == m
单子的形象解释
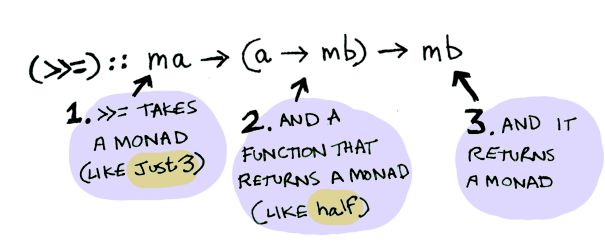
如果说functor是应用一个函数到包裹的值,那么monad则是应用一个返回包裹值的函数到一个包裹的值。
上图表示,首先获得一个Monad,其次定义一个返回Monad的函数如half,最后结果也会返回一个Monad。
这里half函数是输入一个值然后返回一个包裹的值,如果输入的是一个包裹的值,那么代码就不工作了。如下面两幅图所示:
Monad在输入一个包裹值到一个函数的过程中要做到的是:
- 绑定已经解除包裹的值
- 将已经解除包裹的值输入函数
- 一个被重新包裹的值被输出
那么,对一个包裹的值应用多次half函数将是这样的:
小结
Monoid是元素对象的组合的范畴,如果这种元素对象是函数或函子,那么Monad是自函子的组合范畴,Monad也是一种特殊的Monoid子集。
所以正应了那句名言“单子说白了不过就是自函子范畴上的一个幺半群而已(A monad is just a monoid in the category of endofunctors)”。
转载请注明作者Jason Ding及其出处
jasonding.top
Github博客主页(http://blog.jasonding.top/)
CSDN博客(http://blog.csdn.net/jasonding1354)
主页(http://www.jianshu.com/users/2bd9b48f6ea8/latest_articles)
Google搜索jasonding1354进入我的博客主页