第三章 搜索
深度优先搜索与宽度优先搜索
定义
深度优先搜索(DFS)
过程简要来说是对每一个可能的分支路径深入到不能再深入为止,而且每个节点只能访问一次。
宽度优先搜索(BFS)
不考虑结果的可能位置,彻底地搜索整张图,直到找到结果为止。
深度优先 与 宽度优先 实现的本质
深优的本质是递归,自己调用自己。
宽优的本质是利用队列经行的搜索。
深度优先与宽度优先区别
- 深优的话,占内存少,能找到最优解(一定条件下),但能很快找到接近解(优解),可能不必遍历所有分枝(也就是速度快)。时间复杂度高。
- 宽优的话,占内存多,能找到最优解,必须遍历所有分枝。
- 深度优先一般是解决连通性问题,而宽度优先一般是解决最短路径问题。
深度优先搜索
扑克牌问题
假如有编号为1 、2、3 的3 张扑克牌和编号为1 、2 、3 的3 个盒子。现在需要将这3 张扑克牌分别放到3 个盒子里面,并且每个盒子有且只能放一张扑克牌。那么一共有多少种不同的放法呢?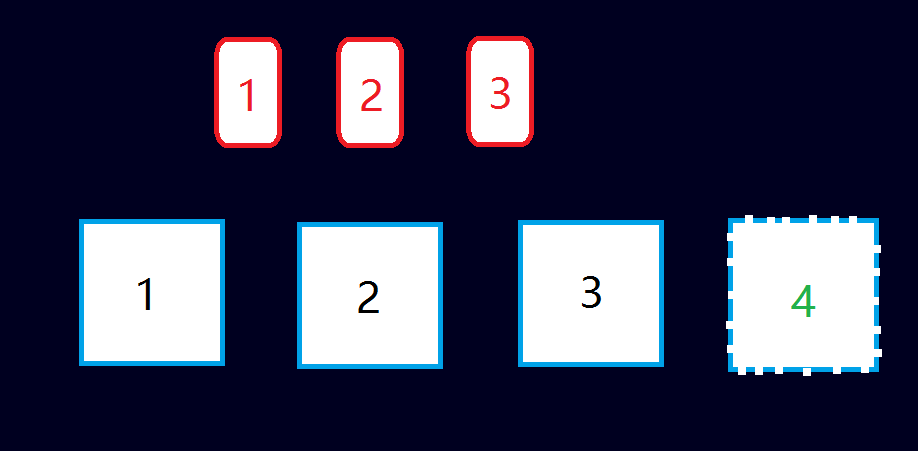
代码如下:
#include
int a[10],book[10],n;
void dfs(int step) { // step表示站在第step个箱子前
int i;
if (step == n+1) { // 成立表示此时所有纸牌都放入箱子中
for (i=1;i<=n;i++)
printf("%d",a[i]);
printf("\n");
return; // 返回最近一次调用dfs函数的地方
}
for (i=1;i<=n;i++) {
if (book[i] == 0) {
a[step] = i;
book[i] = 1; // 表示纸牌已用过
dfs(step + 1); // 移步到下一个箱子
book[i] = 0; // 收回用过的纸牌
}
}
return;
}
int main() {
scanf("%d",&n);
dfs(1); // 开始站在第一个箱子前
return 0;
} 求通往 flag 的最短路程
下题先用深度优先搜索解题,再利用宽度优先搜索解题。
题目:
一只探险队从某一起点出发,寻找某处的宝藏。他们现在有一张藏宝图,为了携带更少的物资,他们需要根据地图求得通向宝藏的最短路程。(注:地图上的黑点代表障碍,无法通过)
地图示例:
深度优先解法:
思路:
利用递归调用一条路走到头,再换一条路。
代码:
#include
int n,m,p,q,min=9999999; // 迷宫大小为 n*m,终点坐标为(p,q),最少步为 min
int a[51][51],book[51][51]; // a代表迷宫 ,book为所过路径标记集
void fun(int x,int y,int step) {
int next[4][2] = {
{0,1}, // 向右走一步(向 y 轴正半轴平移一个单位)
{1,0}, // 向下走一步(向 x 轴正半轴平移一个单位)
{0,-1},
{-1,0}};// 类似上述,分别向左、向上走一步
int tx,ty,k;
if (x == p && y == q) {
if (step < min)
min = step;
// printf("%d\n",step); // 可以利用这条语句进行测试接近解
return; // 返回之前一步
}
for (k=0; k<=3; k++) {
tx = x + next[k][0];
ty = y + next[k][1];
if (tx<1 || tx>n || ty<1 || ty > m)
continue;
if (a[tx][ty] == 0 && book[tx][ty] == 0) {
book[tx][ty]=1; // 标记这个点已经走过
fun(tx,ty,step+1); // 开始尝试下一个点
book[tx][ty]=0; // 尝试结束,取消标记
}
}
return;
}
int main() {
void fun(int x,int y,int step);
int i, j, startx, starty;
scanf("%d %d",&n,&m);
for (i=1; i<=n; i++) // 绘制迷宫,0 为该区域可通行,1 为不可通行
for (j=1; j<=m; j++)
scanf("%d",&a[i][j]);
// 读入起点与终点坐标
scanf("%d %d %d %d",&startx,&starty,&p,&q); // 起点坐标为:(startx,starty), 终点坐标为:(p,q)
book[startx][starty]=1;
fun(startx,starty,0);
printf("%d\n",min);
return 0;
} 宽度优先解法:
思路:
利用队列推进,不断深入。
代码:
#include
struct note { // 定义一个结构体
int x;
int y;
int f;
int s; // 步数
};
int main() {
struct note que[2501]; // 结构体数组
int a[51][51] = {0},book[51][51] = {0};
int next[4][2] = {
{0,1},{0,-1},{1,0},{-1,0}}; // 方向依次右、左、下、上
int head,tail;
int i,j,k,n,m,startx,starty,p,q,tx,ty,flag;
scanf("%d %d",&n,&m);
for(i=1; i<=n; i++)
for(j=1; j<=m; j++)
scanf("%d",&a[i][j]); // 输入地图
scanf("%d %d %d %d",&startx,&starty,&p,&q);
// 初始化结构体数组
head = 1;
tail = 1;
que[tail].x = startx;
que[tail].y = starty;
que[tail].f = 0;
que[tail].s = 0;
tail++;
book[startx][starty] = 1;
flag = 0;
while(head < tail) {
for(k=0; k<=3; k++) {
tx=que[head].x+next[k][0];
ty=que[head].y+next[k][1];
if (tx<1 || tx>n || ty<1 || ty>m) // 判断是否在地图上
continue;
if (a[tx][ty] == 0 && book[tx][ty] == 0) { // 判断是否可通过
book[tx][ty] = 1;
que[tail].x = tx;
que[tail].y = ty;
que[tail].f = head;
que[tail].s = que[head].s+1; // 路程加一,注意对哪一个数值经行加一运算
tail++;
}
if (tx == p && ty == q) { // 判断是否达到终点
flag = 1;
break; // 退出for循环
}
}
if(flag == 1)
break; // 退出while循环
head++;
}
printf("%d",que[tail-1].s); // 注意代表路程的值为哪一个
return 0;
} 测试数据:
6 6 // 地图大小 n行 m列
0 0 0 1 0 0
0 0 1 0 0 1
1 0 0 0 0 0
0 0 0 0 1 0
0 0 1 1 0 0
0 0 0 0 0 1 // 0 为可通过,1 为障碍
1 1 5 5 // 前两个数为起点坐标,后两个为终点坐标
8 8
0 0 1 0 1 0 0 0
0 0 0 0 0 0 1 0
1 0 1 0 0 1 0 0
0 0 1 0 0 0 0 0
0 0 0 0 1 0 0 0
1 0 1 0 0 1 1 1
1 0 0 0 0 1 0 0
0 0 0 1 0 0 0 1
1 1 7 7
12 12
0 0 0 0 0 1 0 0 1 0 0 0
0 1 0 0 0 0 0 0 0 0 1 0
0 0 0 1 0 0 1 0 1 0 0 0
0 0 1 0 0 0 0 0 0 0 0 1
0 1 0 0 0 1 0 0 0 1 0 0
0 0 0 0 1 0 0 0 1 0 0 0
1 0 1 0 0 1 0 0 0 0 1 0
0 0 0 0 0 0 0 1 0 1 0 0
1 0 0 1 0 1 0 1 0 0 0 1
0 0 1 0 0 0 0 0 0 1 0 0
0 0 0 0 0 0 1 0 0 0 0 0
0 1 0 0 1 0 0 0 1 0 0 0
1 1 11 11 总结:
在数据较多时,深度优先搜索可以快速得到接近解,宽度优先搜索可以快速得到优解。(在利用12*12地图时,非常明显)
附:诗
以梦为马(或名:祖国)
——海子
我要做远方的忠诚的儿子
和物质的短暂情人
和所有以梦为马的诗人一样
我不得不和烈士和小丑走在同一道路上
万人都要将火熄灭
我一人独将此火高高举起
此火为大 开花落英于神圣的祖国
和所有以梦为马的诗人一样
我借此火得度一生的茫茫黑夜
此火为大 祖国的语言和乱石投筑的梁山城寨
以梦为马的敦煌——那七月也会寒冷的骨骼
如雪白的柴和坚硬的条条白雪 横放在众神之山
和所有以梦为马的诗人一样
我投入此火 这三者是囚禁我的灯盏 吐出光辉
万人都要从我刀口走过
去建筑祖国的语言
我甘愿一切从头开始
和所有以梦为马的诗人一样
我也愿将牢底坐穿
众神创造物中只有我最易朽
带着不可抗拒的死亡的速度
只有粮食是我珍爱 我将她紧紧抱住
抱住她 在故乡生儿育女
和所有以梦为马的诗人一样
我也愿将自己埋葬在四周高高的山上守望平静的家园
面对大河我无限惭愧
我年华虚度 空有一身疲倦
和所有以梦为马的诗人一样
岁月易逝 一滴不剩 水滴中有一匹马儿一命归天
千年后如若我再生于祖国的河岸
千年后我再次拥有中国的稻田
和周天子的雪山 天马踢踏
和所有以梦为马的诗人一样
我选择永恒的事业
我的事业 就是要成为太阳的一生
他从古至今——"日"——他无比辉煌无比光明
和所有以梦为马的诗人一样
最后我被黄昏的众神抬入不朽的太阳
太阳是我的名字
太阳是我的一生
太阳的山顶埋葬 诗歌的尸体
——千年王国和我
骑着五千年凤凰和名字叫"马"的龙
——我必将失败
但诗歌本身和太阳必将胜利
.
.
.
.
.
我知道我拖了一更。。。。别打脸。。。
以上



