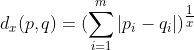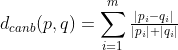数据挖掘原理与实践(4)——相似性度量
大家好,今天我给大家介绍一下什么是相似性度量,其中会重点介绍对象之间的相似性度量,有兴趣的朋友可以好好看一看。相似性度量是衡量变量之间互相关系的强弱、联系紧密程度的重要手段,因此相似性度经常被许多数据挖掘技术使用。而现阶段只有两种度量:属性之间的度量与对象之间的度量。
属性之间的相似性度量
通常,具有若干属性的对象之间的相似性用单个属性的相似性组合来定义,因此我们首先讨论具有单个属性的对象之间的相似性。
1、标称和区间属性
对于由标称属性描述的两个对象来说,什么叫相似?由于标称属性携带了对量的相异性信息,因此我们只能说两个对象有相同的值,要么就没有,通俗地讲,就是“是否”之间的关系。因而在这种情况下,如果属性值相匹配,则相似度定义为1,否则为0;相异度则用相反的方法定义。
对于区间属性,两对象间的相异性的自然度量是它们的值之差的绝对值。在这里,相异度通常在0到![]() 之间。
之间。
下表则汇总了不同属性情况下的相似性度量方法。在该表中,![]() 和
和![]() 是两个属性值,它们具有指定的类型,
是两个属性值,它们具有指定的类型,![]() 和
和![]() 分别是
分别是![]() 和
和![]() 之间的相异度和相似度(分别用
之间的相异度和相似度(分别用![]() 和
和![]() 表示)。
表示)。
| 属性类型 | 相异度 | 相似度 |
|---|---|---|
| 标称型 | ||
| 区间或比率型 |
2、序数和比例数值属性
(1)序数属性
序数属性变量(Ordinal Variable)有分类的和连续的两种。分类序数属性与标称属性类似,但是其排序有一定意义,必须要按照一定次序排列,这有助于记录一些不便于客观度量的主管评价。例如书本上给的例子,职称就是一个分类的序数属性,是按照助教、讲师、副教授、教授的顺序排列的。一个连续的序数属性看上去就像一组未知范围的连续数据,但它的相对未知要比它的实际数值有意义得多。顺序是主要的,而实际的大小则是次要的。
一个序数属性的集合可以映射到一个等级(rank)集合上。例如,若序数属性![]() 有
有![]() 个状态,那么这些有序的状态就可映射为1,2,...,
个状态,那么这些有序的状态就可映射为1,2,...,![]() 的等级,通过等级来描述差异。序数属性
的等级,通过等级来描述差异。序数属性![]() 的差异程度计算方法具体如下:
的差异程度计算方法具体如下:
- 属性
 有
有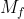 个有序状态,将属性值
个有序状态,将属性值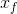 替换为相应的等级
替换为相应的等级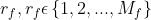 。
。 - 将序数属性等级
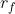 做变换
做变换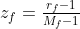 ,映射到区间[0,1]上。
,映射到区间[0,1]上。 - 利用有关间隔数值属性的任一种距离计算公式来计算差异程度。
(2)比例数值属性
比例数值变量(Ratio-scaled Variable)是在非线性尺度上取得的测量值。经典例子包括细胞繁殖增长的数目描述、放射性元素的衰变。
在计算比例数值变量所描述对象间的距离时,有三种处理方法。
- 将比例数值变量当做区间间隔数值变量来进行计算处理。该方法可能导致非线性的比例尺度被扭曲。
- 将比例数值变量看成是连续的序数属性进行处理。
- 利用变换(如对数转换
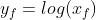 )来处理属性
)来处理属性 的值
的值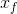 得到
得到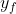 ,将
,将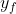 当做间隔数值变量进行处理。这里的变换需要根据具体定义或应用需求而选择log或log-log或其他变换。相对来说,该方法效果较好。
当做间隔数值变量进行处理。这里的变换需要根据具体定义或应用需求而选择log或log-log或其他变换。相对来说,该方法效果较好。
对象之间的相似性度量
在现实生活中,一个对象通常是由多个属性来描述,这一小节讨论得对象之间的相似度度量,即多个属性的相似性度量方法。传统的相似性度量有两种方法:距离度量和相似系数。使用距离度量时,往往将数据对象看成是多维空间中的一个点(向量),并在空间中定义点与点之间的距离。对象之间的相似度计算涉及描述对象的属性类型,需要将不同属性上的相似度整合成一个总的相似度来表示。
1、数值属性相似度度量
(1)距离度量(非常非常重要!这一点几乎必考!)
①Minkowsko(明可夫斯基)距离
对于任意样本对象![]() 与
与![]() ,它们之间的距离定义为
,它们之间的距离定义为
x取值为1,2,![]() 时,分别对应曼哈顿(Manhattan)距离
时,分别对应曼哈顿(Manhattan)距离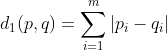 、欧式(Euclidean)距离(即欧几里得距离)
、欧式(Euclidean)距离(即欧几里得距离)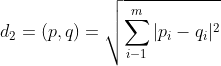 、切比雪夫(Chebyshev)距离
、切比雪夫(Chebyshev)距离![]() 。
。
直接使用Minkowski距离的缺点是量纲或度量单位对聚类结果有影响,为了避免不同量纲的影响,通常需要对数据进行规范化。另外,Minkowski距离没有考虑属性之间的多重相关性,我们可以由此了解一下马氏(Mahalanobis)距离。
②马氏(Mahalanobis)距离
Mahalanobis距离考虑了属性之间的相关性,可以更加准确地衡量多维数据之间的距离。其定义如下:
![]()
其中,A为![]() 的协方差矩阵,
的协方差矩阵,![]() 为协方差矩阵的逆。
为协方差矩阵的逆。
Mahalanobis距离是对Minkowski距离的改进,对于一切线性变换是不变的,克服了Minkowski距离受量纲影响的缺点,也部分地克服了多重相关性。Mahalanobis距离在分类算法中比较常用,但不足在于协方差矩阵难以确定,计算量比较大,不适合大规模数据集。
③Canberra距离(亦叫Lance距离)
Canberra距离定义如下:
Canberra距离可以看成一种相对马氏距离,克服了Minkowski距离受量纲影响的缺点,但同样没有考虑多重相关性。Canberra距离对默认值是稳健的,当两个坐标都接近0时,Canberra距离对微小的变化很敏感。
(2)相似系数
①余弦相似度
余弦相似度忽略各向量的绝对长度,着重从形状方面考虑它们之间的关系。当两个向量方向相近时,夹角余弦值较大,反之则较小。特别地,当两个向量平行的时候,夹角余弦值为1,而正交时余弦值为0。
②相关系数
相关系数是对向量做标准差、标准化后的夹角余弦,表示两个向量的线性相关程度。
③广义Jaccard系数
广义Jaccard系数又称为Tanimoto系数,用EJ表示,广泛用于信息检索和生物学分类中,在二次元性情况下简化为Jaccard系数。
![]()
2、二值属性的相似性
一个二值属性变量(binary variable)只有两种状态:0或1,表示属性的存在与否。一种差异计算方法就是根据二值数据计算。假设二值属性对象![]() 和
和![]() 的取值情况如下表所示:
的取值情况如下表所示:
| 对象q | 对象q | 对象q | 对象q | |
|---|---|---|---|---|
| 对象p | 1 | 0 | 合计 | |
| 对象p | 1 | |||
| 对象p | 0 | |||
| 对象p | 合计 |
其中,![]() 表示对象
表示对象![]() 和
和![]() 均取1的二值属性个数,
均取1的二值属性个数,![]() 表示对象
表示对象![]() 取1而对象
取1而对象![]() 取0的二值属性个数,
取0的二值属性个数,![]() 表示对象
表示对象![]() 取0而对象
取0而对象![]() 取1的二值属性个数,
取1的二值属性个数,![]() 表示对象
表示对象![]() 和
和![]() 均取0的二值属性个数。
均取0的二值属性个数。
二值属性存在对称的和不对称的两种。如果一个二值属性的两个状态值的两个状态值所表示的内容同等重要,则它是对称的,否则为不对称的。基于对称二值变量所计算的相似度称为不变相似性(即变量编码的改变不会影响计算结果)。对于不变相似性,常用简单匹配相关系数来描述对象![]() 和
和![]() 之间的差异程度,其定义如下:
之间的差异程度,其定义如下:
![]()
![]() +
+![]() 为取值不同的属性个数,
为取值不同的属性个数,![]() +
+![]() 表示取值相同的属性个数。
表示取值相同的属性个数。
而对于不对称的二值变量,如果认为取值1比取值0更重要、更有意义,那么,这样的二次变量就好像只有一种状态。在这种情况下,对象![]() 和
和![]() 之间的差异程度评价通常采用Jaccard系数,其定义如下:
之间的差异程度评价通常采用Jaccard系数,其定义如下:
![]()
不同于对称相似性,对象![]() 和
和![]() 均取0的情况被认为不重要,因而忽略了
均取0的情况被认为不重要,因而忽略了![]() 。这种二次型的Jaccard系数经常用于商业零售数据的处理。
。这种二次型的Jaccard系数经常用于商业零售数据的处理。
3、混合属性相似性度量
在实际应用中,数据对象往往用混合类型的属性描述,同时包含了多种类型的属性。这需要将不同类型的属性组合在一个差异度矩阵中,把所有的属性间的差异转换到区间[0,1]中。假设数据集包含![]() 个不同类型的属性,对象
个不同类型的属性,对象![]() 和
和![]() 之间的差异度推广Minkowski距离,定义如下:
之间的差异度推广Minkowski距离,定义如下:
![]()
其中,如果![]() 或
或![]() 数据不存在(对象
数据不存在(对象![]() 或对象
或对象![]() 的属性
的属性![]() 无测量值),或
无测量值),或![]() ,且属性
,且属性![]() 为非对称二值属性,则记为,否则。表示属性
为非对称二值属性,则记为,否则。表示属性![]() 为对象
为对象![]() 和对象
和对象![]() 之间差异(或距离)程度所做的贡献,对象
之间差异(或距离)程度所做的贡献,对象![]() 和对象
和对象![]() 在属性
在属性![]() 上的相异度
上的相异度![]() 可以根据其属性类型进行相应的计算:
可以根据其属性类型进行相应的计算:
- 若属性
 为二元属性或标称属性,
为二元属性或标称属性,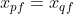 ,则
,则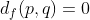 ,否则
,否则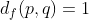 。
。 - 若属性
 为序数型属性,计算对象
为序数型属性,计算对象 和对象
和对象 在属性
在属性 上的秩(或等级)
上的秩(或等级)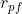 和
和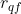 ,
,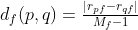 。
。 - 若属性
 为区间标度属性,则
为区间标度属性,则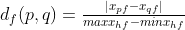 ,这里
,这里 取遍属性
取遍属性 的所有非空缺对象,
的所有非空缺对象,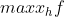 、
、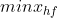 分别表示属性
分别表示属性 的最大值和最小值。
的最大值和最小值。 - 若属性
 为比例数值属性,则通过变换转换为区间标度属性来处理。
为比例数值属性,则通过变换转换为区间标度属性来处理。
4、由距离度量转换来的相似性度量
可以通过一个单调递减函数,将距离转换成相似性度量,相似性度量的取值一般在区间[0,1]之间,值越大,说明两个对象越相似。我们可以采取如下变换:
①采用负指数函数,将距离转换为相似性度量![]() ,即
,即
![]()
②采用距离的倒数最为相似性度量,为了避免分母为0的情况,在分母上加上1,即:
![]()
③若距离在0~1之间,可采用与1的作为相似系数,即
![]()
到此相似性度量这一节的全部内容笔者已经写完了,希望能对大家有所帮助(这堆公式代码真的令人暴躁)。