点云的曲率及计算
目录
- 一、理论知识
-
- 1、曲率类型
- 1.1、主曲率、平均曲率与高斯曲率
- *1.2、表面曲率
- 2、曲率的计算
-
- 2.1、方法一:二次曲面拟合求点云曲率
- 2.2、方法二:利用相邻点的法向量求一点的曲率
-
- 2.2.1、原理概述
- 2.2.2、法曲率的局部拟合
- 2.2.3、欧拉方程最小二乘拟合
- 3、局部曲面类型
- 4、参考文献
- 二、代码实现
-
- 1、二次曲面拟合求点云曲率
- 2、利用相邻点的法向量求一点的曲率
一、理论知识
1、曲率类型
1.1、主曲率、平均曲率与高斯曲率
曲率是曲线弯曲程度的一个度量。平均曲率作为微分几何中一个“外在的”弯曲测量标准,对一个曲面嵌入周围空间(比如二维曲面嵌入三维欧式空间)的曲率进行了区部描述。高斯曲率作为一个描述曲面的凹凸性质的量,当这个量变化程度较大的时候表面曲面内部变化也比较大,这就表明曲面的光滑程度越低。点云中任意一点都存在某曲面 z = r ( x , y ) z=r(x,y) z=r(x,y)逼近该点的邻域点云,一点处的曲率可用该点及其邻域点拟合的局部曲面曲率来表征。通过最小二乘拟合,可以用二次曲面来表征局部区域,计算每点处的主曲率 k 1 , k 2 k_1,k_2 k1,k2、平均曲率 H H H 及高斯曲率 K K K
k 1 , k 2 = H ± H 2 − K (1.1-1) k_1,k_2=H\pm \sqrt{H^2-K}\tag{1.1-1} k1,k2=H±H2−K(1.1-1)
H = E N − 2 F M + G L 2 ( E G − F 2 ) (1.1-2) H=\frac{EN-2FM+GL}{2(EG-F^2)}\tag{1.1-2} H=2(EG−F2)EN−2FM+GL(1.1-2)
K = L N − M 2 E G − F 2 (1.1-3) K=\frac{LN-M^2}{EG-F^2}\tag{1.1-3} K=EG−F2LN−M2(1.1-3)
式中: L = r x x n ; N = r y y n ; E = r x r x ; F = r x r y ; G = r y r y ; r x , r y , r x x , r y y , r x y L=r_{xx}n;N=r_{yy}n;E=r_xr_x;F=r_xr_y;G=r_yr_y;r_x,r_y,r_{xx},r_{yy},r_{xy} L=rxxn;N=ryyn;E=rxrx;F=rxry;G=ryry;rx,ry,rxx,ryy,rxy是曲面的偏微分, E 、 F 、 G E、F、G E、F、G称为曲面的第一基本不变量, L 、 M 、 N L、M、N L、M、N称为曲面的第二基本不变量。
*1.2、表面曲率
主曲率、平均曲率和高斯曲率是数学概念上的曲率(本文后续描述的计算方法皆为计算数学意义上的曲率),表面曲率是点云数据表面的特征值来描述点云表面变化程度的一个概念,与数学意义上的曲率不同。其具体描述和计算方法见:PCL 计算点云法向量并显示,本文不再赘述。
2、曲率的计算
2.1、方法一:二次曲面拟合求点云曲率
在散乱点云中取一个数据点 P i P_i Pi,然后以 P i P_i Pi为中心在点云中均匀地取 n n n个点,这 n n n个点要尽量覆盖整个点云。通过这 n n n个点,利用最小二乘法拟合二次曲面 z ( x , y ) = a x 2 + b x y + c y 2 z(x,y)=ax^2+bxy+cy^2 z(x,y)=ax2+bxy+cy2,解得系数后根据空间曲面曲线的性质计算数据点的高斯曲率和平均曲率。
对于测量点云内任意数据点的 m m m邻域,根据最小二乘原理需使下式取最小值;
Q 2 = ∑ j ( a x j 2 + b x j y j + c y j 2 = z j ) 2 , j ∈ ( 0. k ) (2.1-1) Q^2=\sum\limits_j(ax_j^2+bx_jy_j+cy_j^2=z_j)^2,\\ j\in(0.k)\tag{2.1-1} Q2=j∑(axj2+bxjyj+cyj2=zj)2,j∈(0.k)(2.1-1)
式中, x j , y j , z j x_j,y_j,z_j xj,yj,zj是领域内的点。将式(1)分别对系数求导,使其为 0,得出下式:
{ ∂ Q 2 ∂ a = ∑ j 2 x j 2 ( a x j 2 + b x j y j + c y j 2 − z j ) = 0 ∂ Q 2 ∂ b = ∑ j 2 x j y j ( a x j 2 + b x j y j + c y j 2 − z j ) = 0 ∂ Q 2 ∂ c = ∑ j 2 y j 2 ( a x j 2 + b x j y j + c y j 2 − z j ) = 0 j ∈ ( 0. k ) (2.1-2) \begin{cases} \frac{\partial Q^2}{\partial a}=\sum\limits_j2x_j^2(ax_j^2+bx_jy_j+cy_j^2-z_j)=0\\ \frac{\partial Q^2}{\partial b}=\sum\limits_j2x_jy_j(ax_j^2+bx_jy_j+cy_j^2-z_j)=0\\ \frac{\partial Q^2}{\partial c}=\sum\limits_j2y_j^2(ax_j^2+bx_jy_j+cy_j^2-z_j)=0\\ j\in(0.k) \end{cases} \tag{2.1-2} ⎩⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎧∂a∂Q2=j∑2xj2(axj2+bxjyj+cyj2−zj)=0∂b∂Q2=j∑2xjyj(axj2+bxjyj+cyj2−zj)=0∂c∂Q2=j∑2yj2(axj2+bxjyj+cyj2−zj)=0j∈(0.k)(2.1-2)
由此,解出二次曲面系数。将曲线方程写成曲面参数方程形式:
r ( x , y ) = { X ( x , y ) = x Y ( x , y ) = y Z ( x , y ) = a x 2 + b x y + c y 2 (2.1-3) r(x,y)= \begin{cases} X(x,y)=x\\ Y(x,y)=y\\ Z(x,y)=ax^2+bxy+cy^2\\ \end{cases} \tag{2.1-3} r(x,y)=⎩⎪⎨⎪⎧X(x,y)=xY(x,y)=yZ(x,y)=ax2+bxy+cy2(2.1-3)
若曲面上存在一条曲线 r r r则 r r r的表达式为:
r = r ( x ( t ) , y ( t ) ) (2.1-4) r=r(x(t),y(t))\tag{2.1-4} r=r(x(t),y(t))(2.1-4)
若以 s s s表示曲线 r r r的弧长,则由复合函数求导公式可求得弧长微分公式:
( d s ) 2 = ( d r ) 2 = ( r x d + r y d y ) 2 = r x 2 ( d x ) 2 + 2 r x r y d x d y + r y 2 ( d y ) 2 (2.1-5) (ds)^2=(dr)^2=(r_xd+r_ydy)^2=\\r_x^2(dx)^2+2r_xr_ydxdy+r_y^2(dy)^2\tag{2.1-5} (ds)2=(dr)2=(rxd+rydy)2=rx2(dx)2+2rxrydxdy+ry2(dy)2(2.1-5)
由曲面的第一基本公式可得:
( d s ) 2 = I = E ( d x ) 2 + 2 F d x d y + G ( d y ) 2 (2.1-6) (ds)^2=I=E(dx)^2+2Fdxdy+G(dy)^2\tag{2.1-6} (ds)2=I=E(dx)2+2Fdxdy+G(dy)2(2.1-6)
假如 P P P是曲线 r r r上一点,用 t t t和 n n n分别表示 P P P点的单位切向量和单位法向量,则曲率向量可分解为:
k = d t d s = k n n + k g ( n × t ) (2.1-7) k=\frac{dt}{ds}=k_nn+k_g(n\times t)\tag{2.1-7} k=dsdt=knn+kg(n×t)(2.1-7)
曲线的单位法向量 n n n表示为:
n = r x × r y ∣ r x × r y ∣ (2.1-8) n=\frac{r_x\times r_y}{|r_x\times r_y|}\tag{2.1-8} n=∣rx×ry∣rx×ry(2.1-8)
可得曲面的第二基本公式:
{ I I = − d r ∙ d n = L ( d x ) 2 + 2 M d x d y + N ( d y ) 2 L = r x x ∙ n , M = r x y ∙ n , N = r y y ∙ n (2.1-9) \begin{cases} II=-dr\bullet dn=L(dx)^2+2Mdxdy+N(dy)^2\\ L=r_{xx}\bullet n,M=r_{xy}\bullet n,N=r_{yy}\bullet n\\ \end{cases} \tag{2.1-9} { II=−dr∙dn=L(dx)2+2Mdxdy+N(dy)2L=rxx∙n,M=rxy∙n,N=ryy∙n(2.1-9)
法曲率可表示为:
k = I I I = L + 2 M λ + N λ 2 E + 2 F λ + G λ 2 ; λ = d y d x (2.1-10) k=\frac{II}{I}=\frac{L+2M\lambda+N\lambda^2}{E+2F\lambda+G\lambda^2};\lambda=\frac{dy}{dx}\tag{2.1-10} k=III=E+2Fλ+Gλ2L+2Mλ+Nλ2;λ=dxdy(2.1-10)
处理变量 λ \lambda λ可得到 k n k_n kn的两基根 k 1 , k 2 k_1,k_2 k1,k2,从而根据曲率特性可求得:
高斯曲率
K = k 1 k 2 = L N − M 2 E G − F 2 (2.1-11) K=k_1k_2=\frac{LN-M^2}{EG-F^2}\tag{2.1-11} K=k1k2=EG−F2LN−M2(2.1-11)
平均曲率
H = 1 2 ( k 1 + k 2 ) = E N − 2 F M + G L 2 ( E G − F 2 ) (2,1-12) H=\frac{1}{2}(k_1+k_2)=\frac{EN-2FM+GL}{2(EG-F^2)}\tag{2,1-12} H=21(k1+k2)=2(EG−F2)EN−2FM+GL(2,1-12)
2.2、方法二:利用相邻点的法向量求一点的曲率
2.2.1、原理概述
点云表面上特定点的所有相邻点决定了局部形状。如果通过曲面拟合来估计曲率,可能会产生较大的误差。因此,应该考虑法向量的贡献。为了估计一个点的曲率,我们将只考虑一个相邻点的贡献,这一贡献被转换为一条正截面曲线的构造。我们将构造一个法向截面圆,并根据两个点(目标点和它的一个邻居)的位置和法向向量来估计法向曲率。
2.2.2、法曲率的局部拟合
对于点云中的每个点 p p p,设 p p p点的单位法向量为 N N N,使用点坐标和法向向量来估计点 p p p处的法向曲率的方法如下:
假设 p p p点的附近有 m m m个近邻点, q i q_i qi为点 p p p的第 i i i个近邻点, q i q_i qi的法向量为 M i M_i Mi,设正交坐标系{ p , X , Y , N p,X,Y,N p,X,Y,N}为 p p p点的局部坐标系 L L L, N N N表示 p p p点的法向量。 X X X和 Y Y Y为正交的单位向量。在 L L L中, p , q i , M i p,q_i,M_i p,qi,Mi的坐标可以是(0,0,0), q i q_i qi为( x i , y i , z i x_i,y_i,z_i xi,yi,zi), M i M_i Mi为( n x , i , n y , i , n z , i n_x,i,n_y,i,n_z,i nx,i,ny,i,nz,i)。那么我们可以用一个通过点 p p p的密切圆来估计点 p p p的法曲率 k n i k_n^i kni。图1显示了这些变量的几何关系。
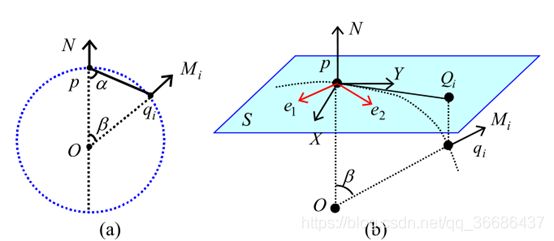
则 p p p相对于 q i q_i qi的发法曲率估计如下:
k n i = − s i n β ∣ p q i ∣ s i n α (2.2-1) k_n^i=-\frac{sin\beta}{|pq_i|sin\alpha}\tag{2.2-1} kni=−∣pqi∣sinαsinβ(2.2-1)
式中: α \alpha α是向量 − N -N −N和 p q i pq_i pqi之间的夹角, β \beta β是向量 N N N和 M i M_i Mi之间的夹角。
等式(2.2-1)的近似值由下式给出:
k n i = − n x y n x y 2 + n z 2 ⋅ x i 2 + y i 2 (2.2-2) k_n^i=-\frac{nxy}{\sqrt{n_{xy}^2+n_z^2}\cdot\sqrt{x_i^2+y_i^2}}\tag{2.2-2} kni=−nxy2+nz2⋅xi2+yi2nxy(2.2-2)
式中: n x y = x i ⋅ n x , i + y i ⋅ n y , i x i 2 + y i 2 , n z = n z , i nxy=\frac{x_i\cdot n_x,i+y_i\cdot n_y,i}{\sqrt{x_i^2+y_i^2}},n_z=n_{z,i} nxy=xi2+yi2xi⋅nx,i+yi⋅ny,i,nz=nz,i。
该方法采用弦、相邻法向量和密切圆,因此我们称之为弦法向量法。这种方法的优点是利用相邻点的法向量来估计一个点的主曲率。
2.2.3、欧拉方程最小二乘拟合
分析了所有法曲率与主曲率的关系。为了用方程(2.2-2)估计一个点的主曲率,相邻点的所有坐标被转换成局部坐标系的坐标。给定点 p p p处的法向量 N N N:
N = ( n x , p , n y , p , n z , p ) N=(n_{x,p},n_{y,p},n_{z,p}) N=(nx,p,ny,p,nz,p)
以及
X = ( − s i n φ , c o s φ , 0 ) (2.2-3) X=(-sin\varphi,cos\varphi,0)\tag{2.2-3} X=(−sinφ,cosφ,0)(2.2-3)
Y = ( c o s ψ s i n φ , c o s ψ c o s φ , − s i n ψ ) (2.2-4) Y=(cos\psi sin\varphi,cos\psi cos\varphi,-sin\psi)\tag{2.2-4} Y=(cosψsinφ,cosψcosφ,−sinψ)(2.2-4)
式中: ψ = a r c c o s ( n z , p , φ = a r c t a n ( n y , p / n x , p ) ) \psi=arccos(n_{z,p},\varphi=arctan(n_{y,p}/n_{x,p})) ψ=arccos(nz,p,φ=arctan(ny,p/nx,p)),点 p p p的局部坐标系 L L L变成如图1(b)所示的{ p , X , Y , Z p,X,Y,Z p,X,Y,Z}。
设 S S S为通过点 p p p的平面,法向量为 N N N,设 e 1 e_1 e1和 e 2 e_2 e2为点 p p p处的主方向,对应主曲率 k 1 k_1 k1和 k 2 k_2 k2,二者未知。设未知参数 θ \theta θ为向量 e 1 e_1 e1和 e 2 e_2 e2的夹角, θ i \theta_i θi是矢量 X X X和矢量 p Q i pQ_i pQi之间的夹角,其中 p Q i pQ_i pQi是矢量 p q i pq_i pqi在平面 S S S上的投影。 θ i \theta_i θi可以用点 q i q_i qi的局部坐标来计算。
根据欧拉公式,法曲率和主曲率有以下关系:
k n i = k 1 c o s ( θ i + θ ) + k 2 s i n 2 ( θ i + θ ) , ( i = 1 , 2 , ⋯ , m ) (2.2-5) k_n^i=k_1cos(\theta_i+\theta)+k_2sin^2(\theta_i+\theta),\\(i=1,2,\cdots,m)\tag{2.2-5} kni=k1cos(θi+θ)+k2sin2(θi+θ),(i=1,2,⋯,m)(2.2-5)
式中: θ i + θ \theta_i+\theta θi+θ为点 p p p过 q i q_i qi的法截线的切线与主方向的夹角。
该任务可以写成一个优化问题:
min k 1 , k 2 , θ ∑ i = 0 m [ k 1 c o s 2 ( θ i + θ ) + k 2 s i n 2 ( θ i + θ ) − k n i ] 2 (2.2-6) \min\limits_{k_1,k_2,\theta}\sum_{i = 0}^{m}[k_1cos^2(\theta_i+\theta)+k_2sin^2(\theta_i+\theta)-k_n^i]^2\tag{2.2-6} k1,k2,θmini=0∑m[k1cos2(θi+θ)+k2sin2(θi+θ)−kni]2(2.2-6)
因为, k 1 c o s 2 ( θ i + θ ) + k 2 s i n 2 ( θ i + θ ) = c o s 2 θ i ( k 1 c o s 2 θ + k 2 s i n 2 θ ) + 2 c o s θ i s i n θ i ( k 2 c o s θ s i n θ − k 1 c o s θ s i n θ ) + s i n 2 θ i ( k 1 s i n 2 θ + k 2 c o s 2 θ ) k_1cos^2(\theta_i+\theta)+k_2sin^2(\theta_i+\theta)=cos^2\theta_i(k_1cos^2\theta+k_2sin^2\theta)+2cos\theta_isin\theta_i(k_2cos\theta sin\theta-k_1cos\theta sin\theta)+sin^2\theta_i(k_1sin^2\theta+k_2cos^2\theta) k1cos2(θi+θ)+k2sin2(θi+θ)=cos2θi(k1cos2θ+k2sin2θ)+2cosθisinθi(k2cosθsinθ−k1cosθsinθ)+sin2θi(k1sin2θ+k2cos2θ)公式(2.2-6)可以写成矩阵形式
min μ ∣ ∣ M μ − R ∣ ∣ 2 (2.2-7) \min\limits_{\mu}||M\mu-R||^2\tag{2.2-7} μmin∣∣Mμ−R∣∣2(2.2-7)


在(2.2-7)的最小二乘拟合之后,可以相应地获得 μ \mu μ的估计值。可以推断出:

所以主曲率 k 1 k_1 k1和 k 2 k_2 k2是矩阵 W = [ A B B C ] W=\left[ \begin{matrix} A & B \\ B & C \\ \end{matrix} \right] W=[ABBC]
的特征值,把 W W W的单位特征向量从局部坐标系 L L L变换到全局坐标系,就得到主方向向量。
3、局部曲面类型
根据微分几何性质可知,主曲率是采样点局部性状的体现。高斯曲率 K K K是主曲率的乘积,根据其符号可以确定曲面上点的性质, K > 0 K>0 K>0表明该点是椭圆点, K = 0 K=0 K=0为抛物点, K < 0 K<0 K<0则 为双曲点 (K
| 类型序号 | 高斯曲率 | 平均曲率 | 几何意义 | 曲面类型 |
|---|---|---|---|---|
| 1 | K=0 | H=0 | 平面 | 平面 |
| 2 | K=0 | H>0 | 脊 | 点局部为凸,在一个主方向上为平 |
| 3 | K=0 | H<0 | 谷 | 点局部为凹,在一个主方向上为平 |
| 4 | K<0 | H>0 | 鞍形脊 | 点在大部分方向上为凸,在小部分方向上为凹 |
| 5 | K<0 | H<0 | 鞍形谷 | 点在大部分方向上为凹,在小部分方向上为凸 |
| 6 | K>0 | H>0 | 峰 | 点在所有方向上均为凸 |
| 7 | K>0 | H<0 | 阱 | 点在所有方向上均为凹 |
4、参考文献
[1] 微分几何——彭家贵,第五版
[2] ZHANG Xiaopeng, LI Hongjun, CHENG Zhanglin. Curvature estimation of 3D point cloud surfaces through the fitting of normal section curvatures[C]. Proceedings of AsiaGraph, Tokyo, Japan, 2008:72-79.
二、代码实现
1、二次曲面拟合求点云曲率
二次曲面拟合求曲率的方法即为本博客理论知识部分描述的算法原理。其具体实现代码见:二次曲面拟合求点云的曲率
2、利用相邻点的法向量求一点的曲率
利用邻域点法向量求一点的曲率即为PCL中求解主曲率的方法见:PCL 计算点云的主曲率
其详细计算过程的代码实现见:利用相邻点的法向量估计一个点的主曲率